逃逸飞行器轨迹鲁棒性快速评估及制导

李 臻，杨 彪，荆武兴，高长生，常武权

(1.哈尔滨工业大学航天工程系，哈尔滨150001；2.北京宇航系统工程研究所，北京100076)

1 引言

逃逸飞行器是载人航天器上用以保障航天员生命安全的一个重要组成部分。国外最早在开展阿波罗计划时便已经进行相关研究[1]；国内在设计CZ-2F载人运载火箭时也开展过相关试验工作[2-4]。逃逸飞行器设计过程涉及逃逸模式选定、逃逸能力评估等各个方面。朱仁璋等[5]进行过对神舟系列飞船的分离动力学分析，许锋等[6]研究了逃逸主推力及结构弹性变形对安全逃逸距离的影响，李家文等[7]分析了各种工况下爆炸冲击波对逃逸飞行器的损坏情况。而关于逃逸飞行器轨迹设计与制导方法，目前鲜见文章详细论述。

考虑到逃逸飞行器逃逸过程中，各种偏差对轨迹鲁棒性和制导会带来较大影响。针对该类飞行器，本文利用误差传播法与线性二次调节器(Linear Quadratic Regulator，LQR)控制方法，提出一种工程实用性强的轨迹设计与制导方法。其中，误差传播法用于轨迹鲁棒性快速评估，难点在于确定时变系统状态转移矩阵。陈国强[8]最早在研究引力异常对惯性制导影响时，给出过只考虑重力场作用时，状态转移矩阵的近似解析解；郑伟[9]在研究地球物理摄动对导弹命中精度影响时，采用伴随矩阵近似求解该矩阵解析解。而LQR理论最早用于再入飞行器的弹道跟踪中，Dukeman[10]，Zhou等[11]设计的状态调节器取得了良好效果；张大元等[12]针对防空导弹，也设计过基于LQR的弹道跟踪制导律。

本文针对逃逸过程中的偏差影响，先利用误差传播法快速评估轨迹鲁棒性得到标称轨迹，进而采用LQR方法进行轨迹跟踪制导。本文在设计误差传播法时，系统模型复杂度增加，区别于文献[8]、[9]，不再能给出一个状态转移矩阵的解析解形式，因此采用数值解求解办法，以较短时间获得较高计算精度；此外，在不同背景下，LQR应用方式略有区别，通过合理减少状态参数个数，成功实现多变量跟踪。

2 逃逸飞行器模型及轨迹设计

2.1 动力学模型

本文研究对象为具有轴对称布局的逃逸飞行器。其直到救生塔分离前的这一飞行过程，可分为主动段和被动段，被动段结束时需要满足分离约束。其工作时序如下：在接收到箭体分离指令后，逃逸飞行器从运载火箭主体脱离，逃逸主发动机工作，经过短时间延迟t0后，开始调整飞行器姿态。主发动机只能工作小段时间，t2时间后进入无动力被动飞行段。飞行器的制导只在主动段进行，经过一段时间的被动飞行后，救生塔准备分离。

地面发射系下建立逃逸飞行器的精确动力学模型见式(1)。

式中，为地面发射系下速度、加速度；aT为推力加速度，主动段t2时间内沿弹体方向为一固定值，被动段内大小为0；aR为气动加速度，为简化分析本文不考虑侧向运动；g为重力加速度，考虑到J2扰动项；ak、aω分别为科氏加速度与离心加速度，由地球自转引起。各项在地面发射系下具体表达式如式(2)。

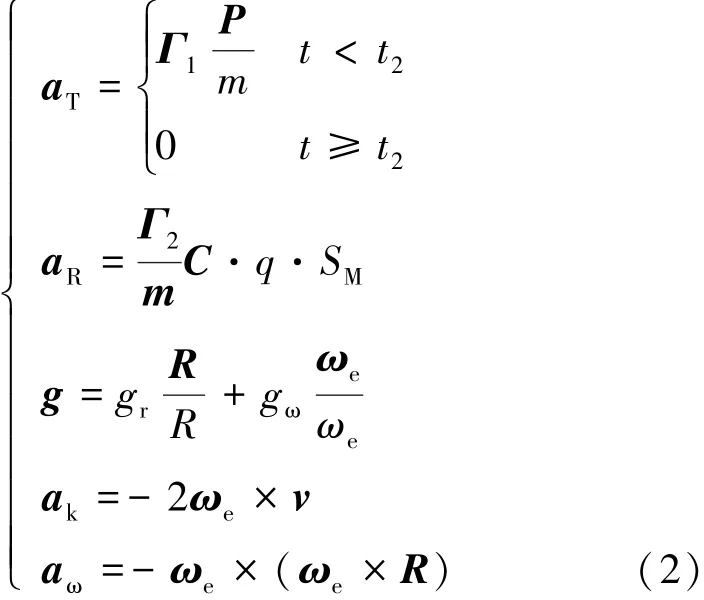
其中引力相关项表达式见式(3)[9]。

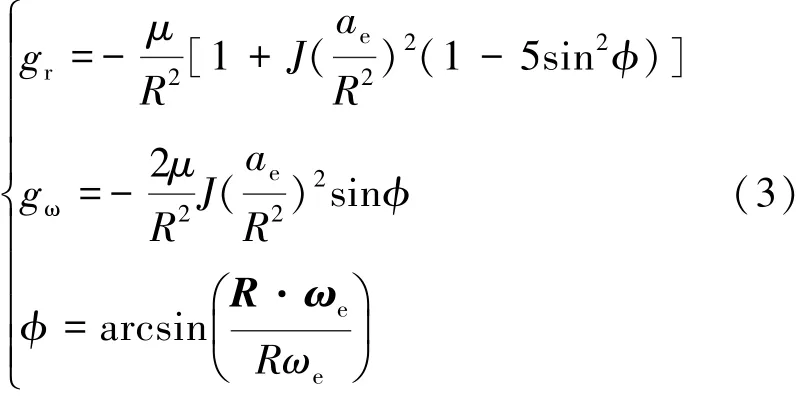
以上方程中，P为体系下轴向推力矢量；C为气流系下气动系数矩阵，包含阻力系数Cx和升力系数Cy，可当作迎角α和马赫数Ma的函数，用fxMa，α()与gyMa，α()拟合；q为动压，SM为逃逸飞行器特征面积；gr与gω分别为重力加速度在径向与自转方向上的分量；R为地心至飞行器矢量，μ为地球引力常量，J为地球扁率修正项；ae为地球赤道半径；φ为飞行器处地心纬度。

Γ1与Γ2分别为弹体系与气流系到发射系的坐标转换阵。为简化研究，可假定飞行器沿射面内飞行不考虑滚转、偏航，则有式(4)：

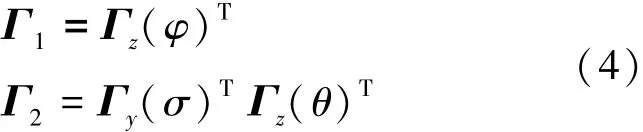
φ为弹道倾角，近似有φ＝α＋θ；σ与θ分别为速度偏角与速度倾角，见式(5)。

2.2 误差线性化模型

在小扰动假设条件下，每时刻飞行器状态误差为小量。针对逃逸飞行器动力学模型式(1)，以时间为自变量，可在标准弹道上特征点附近线性化展开，见式(6)。

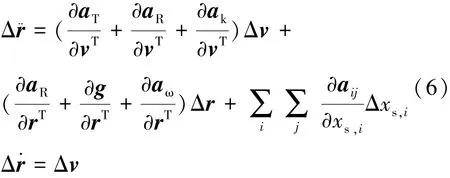
Δxs，i为第i个状态偏差，aij是与该状态相关的第j个加速度项。

取系统状态量χ ＝[ΔrΔv]T，上式的状态空间表达式见式(7)：

用A来表示上式中状态量前的系统矩阵，见式(8)。

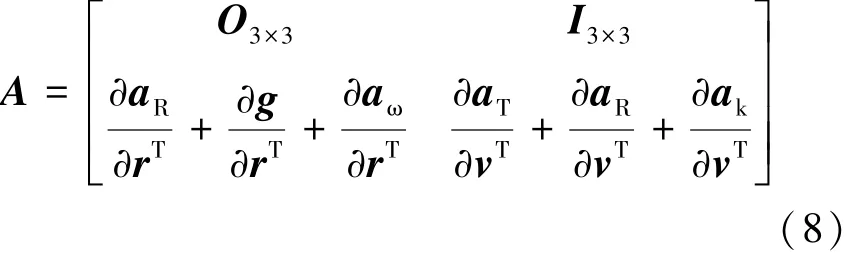
根据不同任务需求，状态偏差Δxs，i可以取不同值。例如，在进行制导系统设计时，需要得到迎角指令修正量，取为式(9)：

此时，式(7)中最后一项可看作控制输入，在进行误差传播分析时，考虑质量偏差、2种气动系数偏差、大气密度偏差影响，则取式(10)：

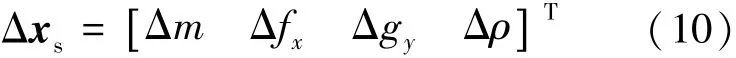
最后一项又可看作状态摄动项。在不同的任务中，系统矩阵A形式相同，下面将依次分析A中各项具体表达形式。

1)引力加速度偏差。引力加速度与位矢r相关，用R0表示地心至发射系原点矢量，则有式(11)。

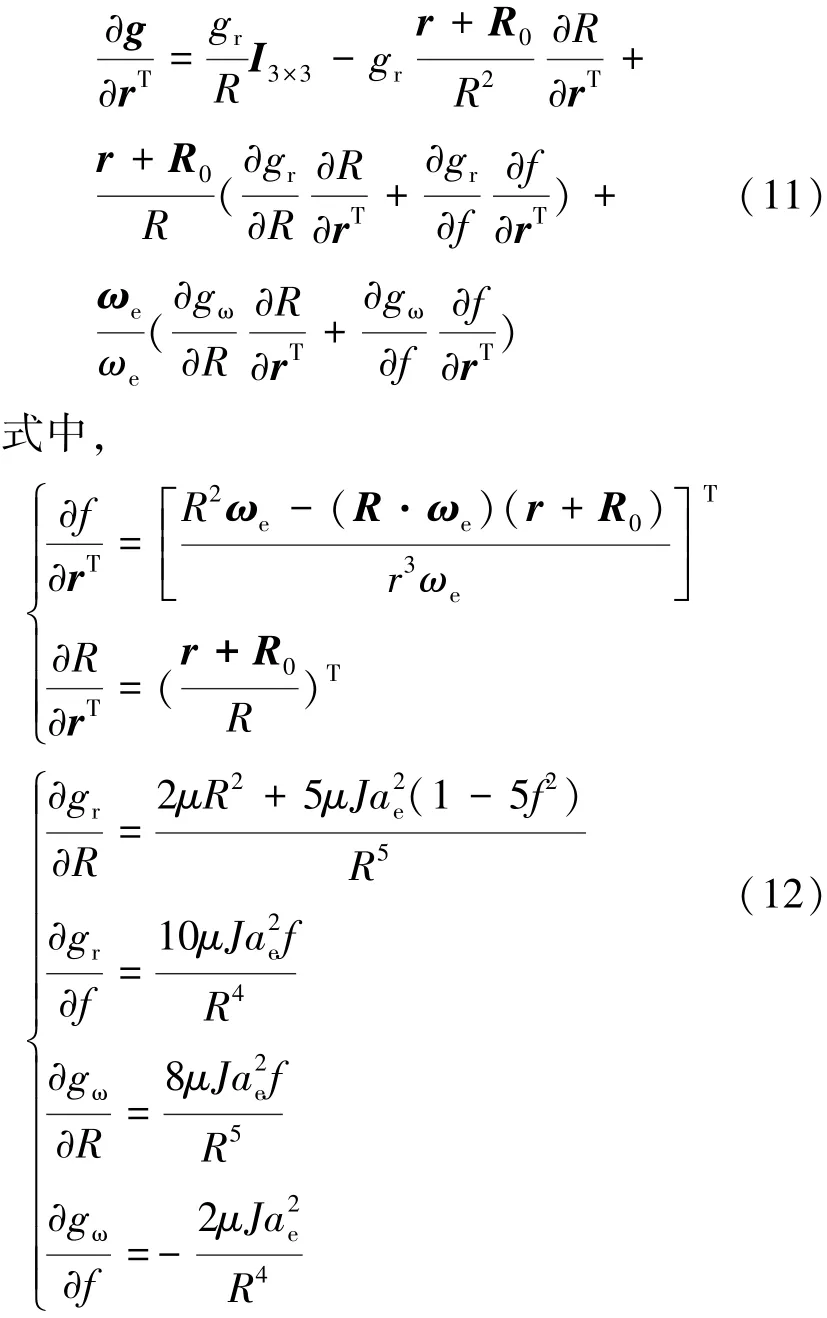
由于J2扰动导致的误差是微小的，因此可忽略其影响，此时有式(13)。

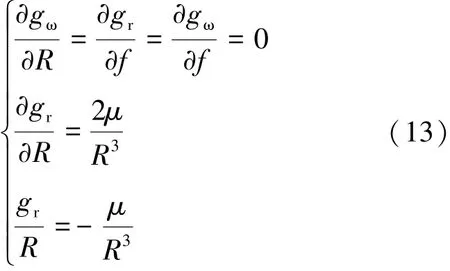
式(11)可推导为式(14)：

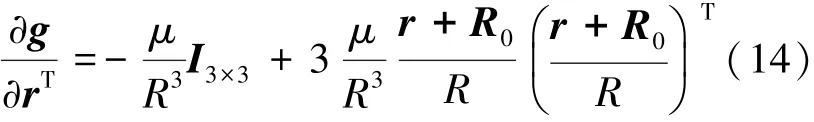
2)科氏加速度偏差。记ωe×为ωe的反对称阵，见式(15)：

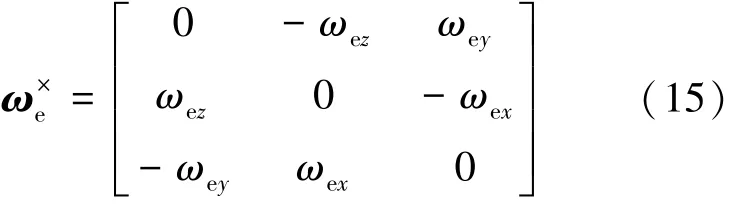
于是科氏加速度又可以表示为式(16)。

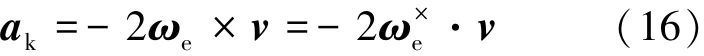
对速度偏导可得式(17)。

3)离心加速度偏差。利用反对称阵，离心加速度可写为式(18)：

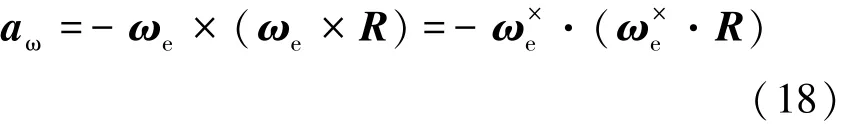
由于R＝r＋R0，则有式(19)。

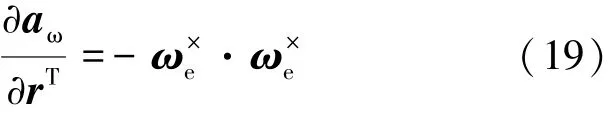
4)推力加速度偏差。推力加速度矢量形式在式(2)中可见，其中弹道倾角φ与速度v相关，见式(20)。

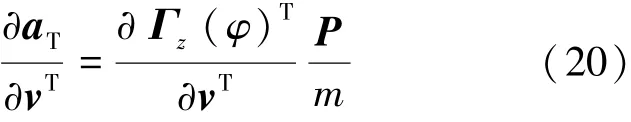
5)气动加速度偏差。气动加速度与位矢r、速度v均相关，不考虑偏航运动下得式(21)：

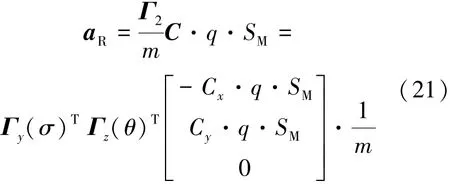
在飞行中大气密度模型见式(22)[12]：

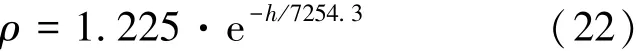
则气动加速度对位矢的偏导可以表示为式(23)。

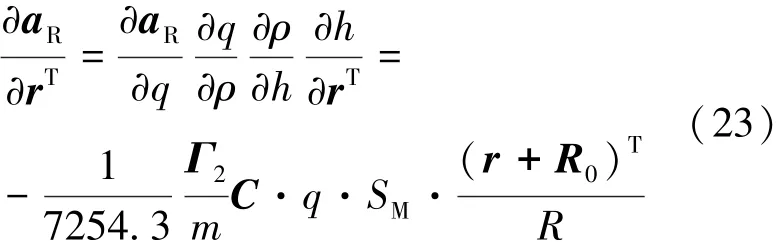
注意到σ、θ、q、C均是速度v的函数，则气动加速度对速度的偏导可以表示为式(24)。

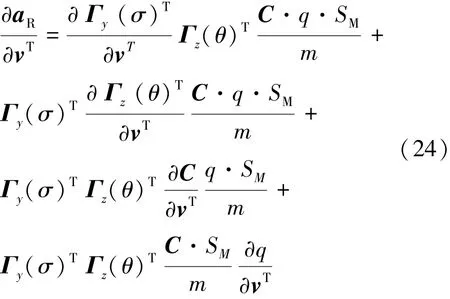
至此，得到了系统矩阵A的完整表达形式。

2.3 逃逸轨迹设计

在工程任务中，轨迹设计之初依据经验一般给出如图1所示的指令迎角，迎角极值在区间-1°到-10°内待定。自逃逸开始到t0段，迎角保持为0；t0至t1段，设计迎角以固定斜率4°/s线性减少直到极值α；t2为飞行器逃逸主推发动机关机点时刻，设计迎角在t1至t2段保持不变；t3为主推发动机关机后5 s，在此处迎角回归至0并一直持续到被动段飞行结束时刻t4。

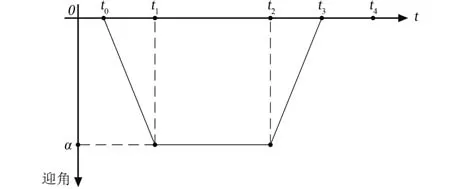
图1 指令迎角规律Fig.1 Profile of attack angle

为确定合适最大指令迎角，需要先在不考虑偏差时，遍历搜索出末态满足二次分离指标的迎角极值子区间。然后进行弹道鲁棒性评估，在考虑偏差干扰下，通过打靶筛选出仍能满足二次分离点指标且裕度较大的迎角极值。选定合适值后，在主动段设计制导律，保证在偏差作用下，能跟踪上主动段部分标称轨迹，这样在被动段自由飞行后末态才有可能满足末态二次分离要求。

利用推导得出的误差线性化模型，应用于弹道评估与制导两部分，轨迹设计中联合使用误差传播法与LQR控制律将体现出极高的计算效率。

3 轨迹鲁棒性评估及制导

3.1 基于误差传播模型的鲁棒性分析

误差传播模型用来快速计算有偏差情况下末端状态。基本原理是根据以位置偏差、速度偏差为状态量的系统状态空间表达式，求解其状态转移矩阵的解析解，进而得出状态偏差在任意时刻的通解。考虑在质量偏差、气动系数偏差、大气密度偏差下，系统产生的偏差。按照式(7)，取：Δxs＝

可得摄动状态方程式(25)。

系统矩阵A由式(8)得出，而摄动项V在此处为式(26)：

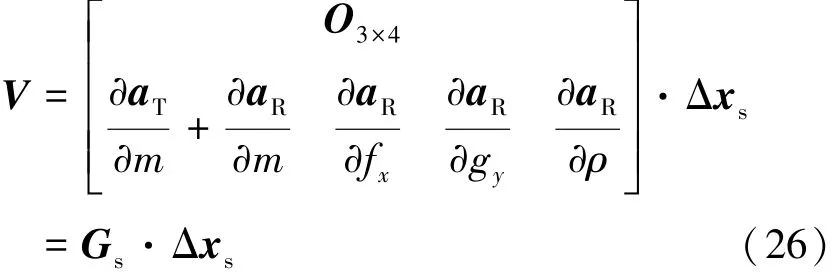
该系统为线性时变系统，其状态转移矩阵Φ是系统矩阵A的函数，满足式(27)：

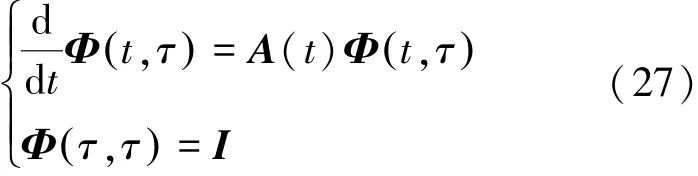
对于简单的时不变系统，状态转移矩阵可通过矩阵指数函数快速得到。而对于时变系统，通过共轭法来求解状态传递函数。

式(27)所代表的摄动系统中，共轭方程可写为式(28)。

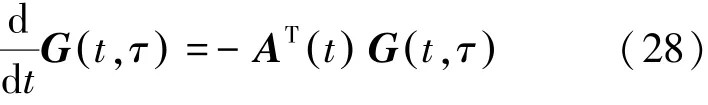
G (t，τ)为引入的共轭矩阵，可得式(29)。

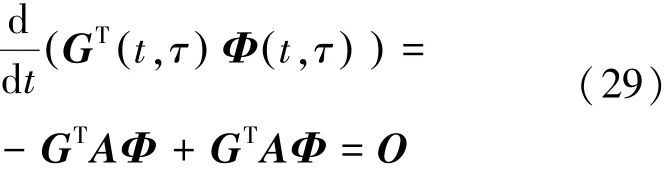
于是有式(30)。

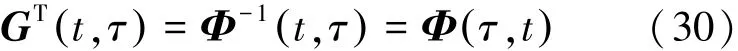
对方程组式(31)：

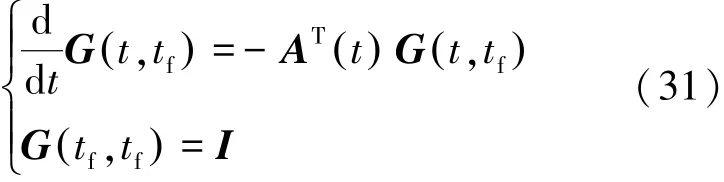
从tf到t0一次积分，即可得到该时间区间内G t，tf( ) 值，由式(32)：

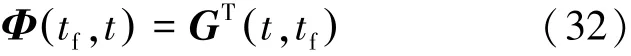
在初始偏差条件χ(t0)＝χ0下，根据微分方程理论，可得偏差状态系统通解为式(33)：

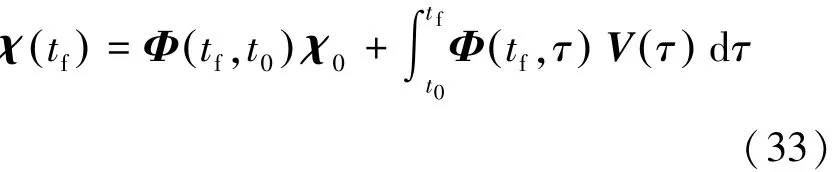
若摄动项V中状态偏差源Δxs不是时间的函数，记为式(34)：

系统末态误差为式(35)：

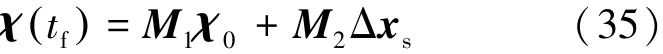
设X*为系统在无偏差状态下的末状态，那么存在偏差时，系统末状态为式(36)：

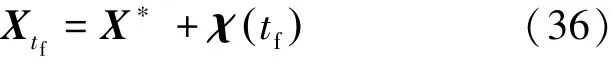
通过已经计算好的系数矩阵M1与M2，在误差源不同取值下可利用式(36)快速计算新的末状态参数。

弹道鲁棒性分析过程中，一般直接采用解析法来完成打靶，需要将偏差项直接代入原系统动力学模型中积分，多次计算速度受限于积分过程。使用误差传播法，在确定一种模型的系数矩阵后，通过矩阵乘法能直接得出末态参数，这种方式打靶效率显然高于传统的解析法。具体计算流程如图2所示。

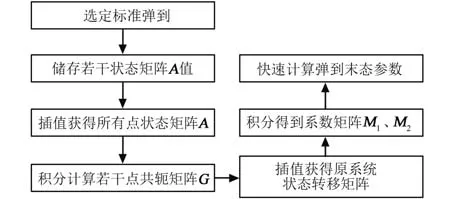
图2 误差传播法计算流程Fig.2 Flowchart of the error propagation method

3.2 LQR制导模型

实际轨迹在各种误差影响下不可避免地会偏离标称轨迹，采用LQR方式进行制导，通过以调整指令迎角的方式，使得实际轨迹能够跟踪上标准轨迹。采用式(9)表达形式，并引入控制量u＝Δxs＝Δα。

这里迎角偏差作为控制量，于是偏差系统状态方程写为式(37)：

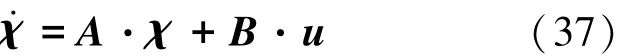
其中矩阵B满足式(38)：

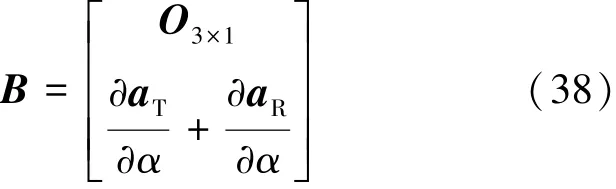
对于上述系统，求解控制量u，使得χ＝O即可实现对标准轨迹的精确跟踪。

系统状态χ描述了飞行轨迹位置偏差、速度偏差共计6个量。但是考虑到，飞行器无侧滑运动在射面内飞行，因此状态χ中z方向运动量，不关心也不可控。此外，x方向位置代表了射程，在之后计算实际轨迹上各点的反馈矩阵时，会利用其在标称轨迹上插值，使得每一时刻下Δx＝0。从系统状态空间中去除x、z、vz，新的状态量为式(39)：

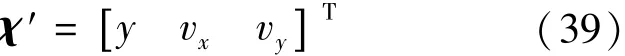
相应的状态空间变为式(40)：

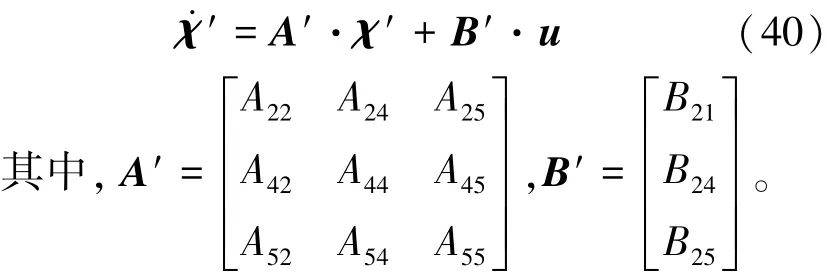
该系统最优控制性能指标函数为式(41)：

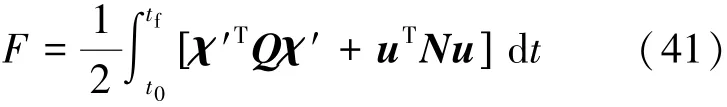
其中Q与N分别为状态向量与控制向量的加权矩阵。在工程实践中，Q、N阵常取对角矩阵，这里χ′为三维量，u为一维量，所以可以令：

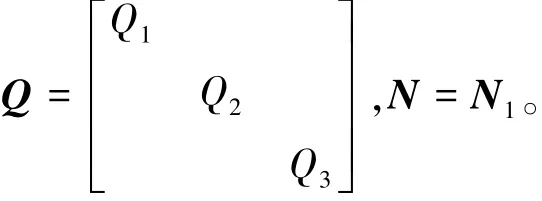
性能指标改写为式(42)：

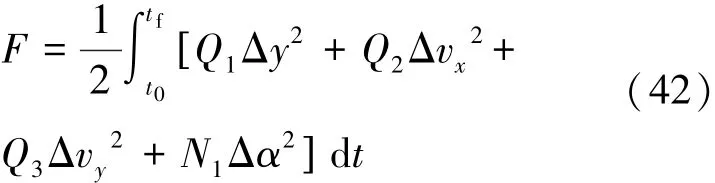
根据式(43)所示Bryson法则：

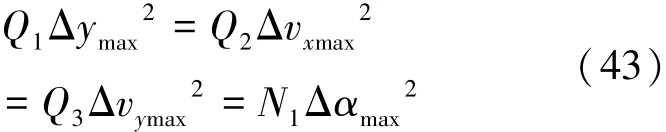
这里取：Δymax＝30 m，Δvxmax＝1 m/s；Δvymax＝10 m/s，Δαmax＝5°。

相应的，Q1＝1，Q2＝900，Q3＝9，N1＝36。

为了让性能指标F最小，最优控制量应符合式(44)：

其中，时变矩阵P是式(45)所示Riccati方程的解：

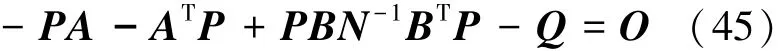
在得到u*即Δα*后，进一步算得当前需要的指令迎角，见式(46)：

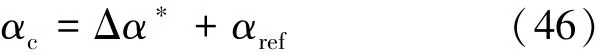
式中αref为标称轨迹下指令迎角。

在标称轨迹上，每一个制导周期内取一个特征点，在各特征点附近认为系统矩阵A、B保持不变。计算得到各特征点下的反馈阵K后，预先装订成反馈增益参数。对于逃逸飞行器，在飞行全过程中，每一个制导周期来临时，根据当前射程x，找到标称轨迹上相邻的两个特征点，利用这两点的反馈增益系数，插值计算得到当前射程下对应的反馈增益系数作为该制导周期内通用的反馈增益系数。

4 算例及仿真

相关仿真参数由表1给出，二次分离点指标见表2，参数偏差取值见表3。

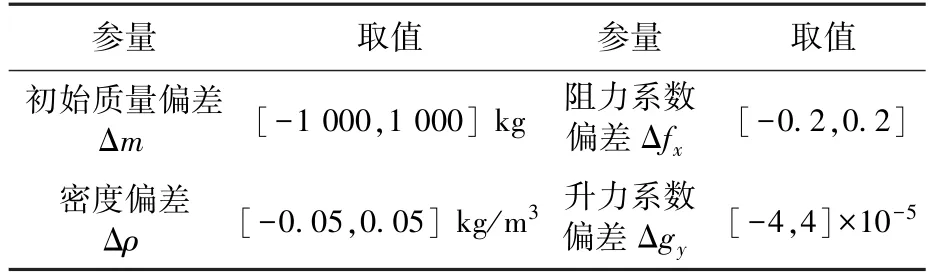
表3 参数偏差Table 3 Parameter deviations

气动系数拟合函数为式(47)：

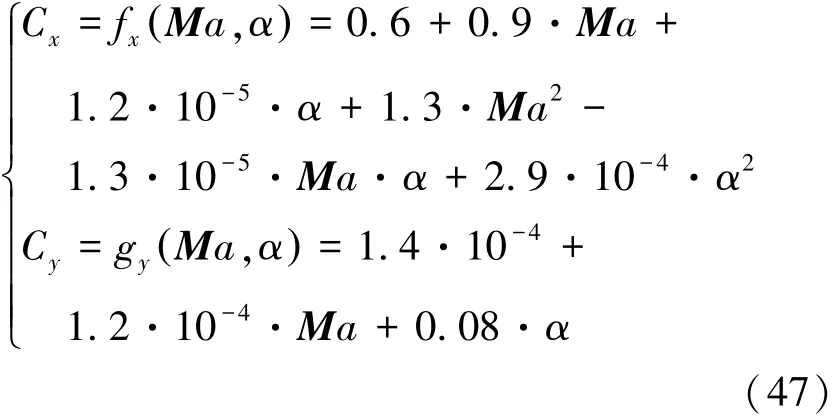
第一步，在不考虑偏差下遍历搜索-1°到-10°区间，找到满足末态指标的子区间。该问题中，最大指令迎角在区间 [-6°，-4°]时，能满足二次分离指标。 -4°、-5°、-6°情况下的末态参数在表 4 中可见，4种主要参数满足了表2要求的约束条件。

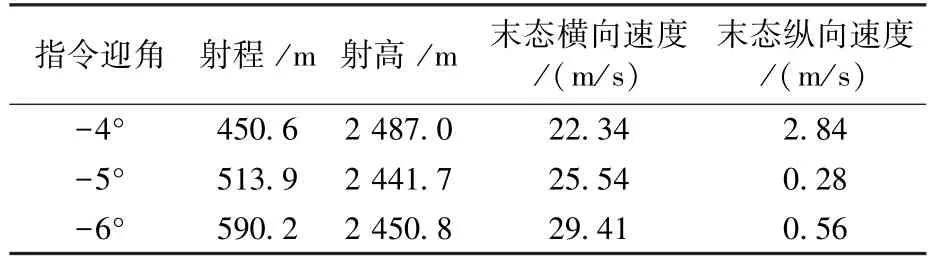
表4 3种指令迎角下仿真结果Table 4 Simulation results under 3 angles of attack

第二步，分别计算以上3种情况在被动段的误差传递系数。被动段初值使用各迎角在不考虑偏差下主动段飞行结束时刻值。以指令迎角为-4°时为例，被动段初始状态为：[r0v0]T＝[132.06 1605.93-0.25 39.00 182.97-0.047]T，相应误差传播系数为：

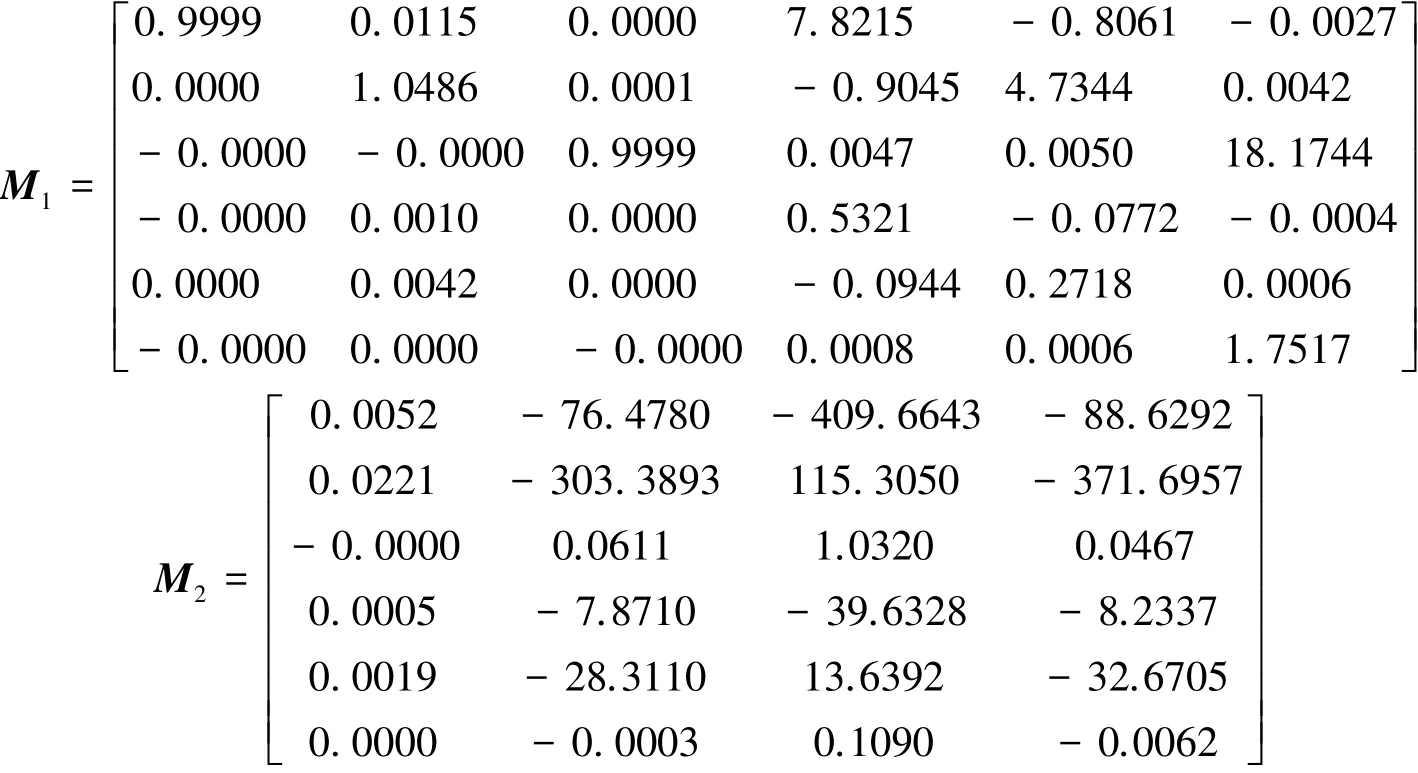
第三步，利用误差传递系数，由式(36)快速计算末态参数。考虑到主动段在进行制导后，被动段的初始参数相比标准状态不可避免地会有差异。χ0取被动段标准状态下初值10%范围内随机大小的偏差。Δxs取参数偏差区间内随机大小的偏差。进行N＝10 000次打靶，绘制各指令迎角下的射程射高散布、横向速度纵向速度散布，见图3～图5。

此外，为了验证这种算法正确性，这里在固定的极限初态偏差χ0和参数偏差Δxs下，对比分析2种算法下仿真结果：χ0＝[Δr0Δv0]T＝[-13.21 160.59-0.03-3.90 18.30 0.00]T；Δxs＝[ΔmΔfxΔgyΔρ]T＝[-1000 0.2 4×10-50.05]T。

在-4°最大迎角下，分别使用解析法和误差传播法计算系统末态参数如下：X1tf＝[370.0270 2618.6789-1.1965 16.9327-1.8686-0.1214]T；[365.5944 2633.1293-1.1561 16.3831-0.9445-0.1183]T。

图3 -4°指令迎角下散布规律Fig.3 Dispersion characteristic under-4°angle of attack

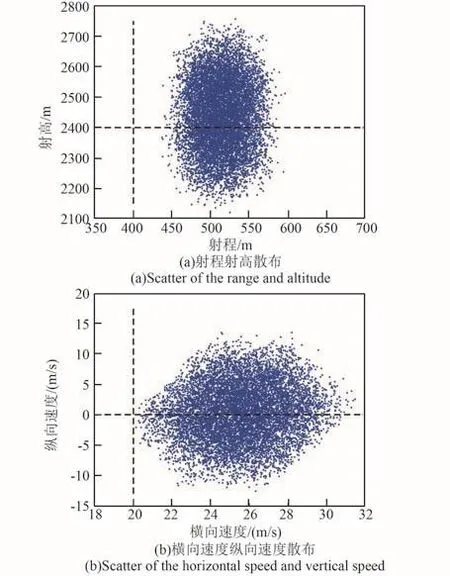
图4 -5°指令迎角下散布规律Fig.4 Dispersion characteristic under-5°angle of attack

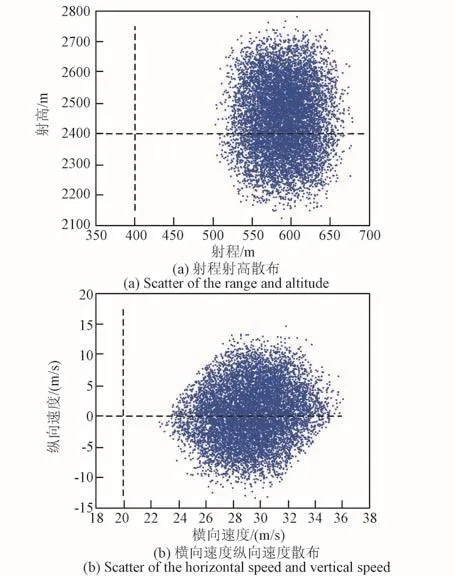
图5 -6°指令迎角下散布规律Fig.5 Dispersion characteristic under-6°angle of attack

无偏差情况下，系统的末态参数为：X0tf＝[447.1818 2475.8783-1.2149 22.1663 2.2454-0.1256]T

误差传播法相对解析法的计算误差与计算时间已记录在表5中。

表5 算法结果比较Table 5 Comparison of algorithms

解析法下计算结果可以视为标准值，采用误差传播得到的结果基本与之接近。从表5中数据可以看出，x、z方向上各项相对误差均在4%以内；y方向速度相对误差较大，但绝对误差在可接受范围内。这种情况可能来自于模型的缺陷，误差传播法模型基于误差线性化模型得到，在基准量小时，引入一定误差源后，若状态偏差大，则线性化效果不理想；相反，基准量越大，线性化效果越好。因此，对比无偏差下末态参数可以发现，该系统中y方向位置相对误差最小，只有0.5%；z方向位置、速度基准值较小，但在该模型中z方向运动可以忽略，误差源并不会使其状态偏差过大，故相对误差也较小，约为3%；y方向速度基准值小，受误差源影响，故相对误差较大。在用于多次打靶时，采用误差传播法计算速度明显快于解析法。以上结果，验证了误差传播法的准确性与快速性。

第四步，在存在偏差时仍要满足二次分离指标，打靶后各散点应该分布在散布规律图中虚线分割后的右上侧区域内。进行多轮仿真试验，综合各迎角下散布情况，选择满足末态分离要求概率更高的一种迎角作为标称轨迹的指令最大迎角。以3轮N＝10 000次的快速打靶为例，在随机大小参数偏差影响下，3种指令迎角工况中，能够满足末态约束要求的概率如表6所示。可以看出，在偏差源影响下，选择-4°作为标称轨迹的指令最大迎角时存在55%的成功率完成末态分离指标，相比其他角度下轨迹，抗干扰能力更强，鲁棒性更高。因此，通过这种方式就可以筛选出更理想的标称轨迹。

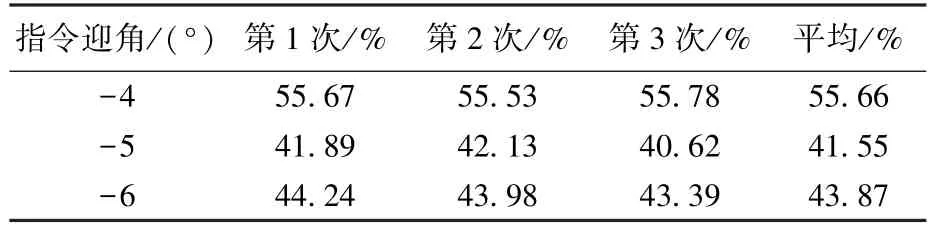
表6 多次打靶成功率统计Table 6 Success rate of multiple shooting

第五步，在存在偏差情况下，使用LQR制导律在主动段跟踪标称轨迹，被动段自由飞行。这里取如下偏差进行仿真： [ΔmΔfΔgΔρ]Txy＝[800 0.08 4×10-50.01]T

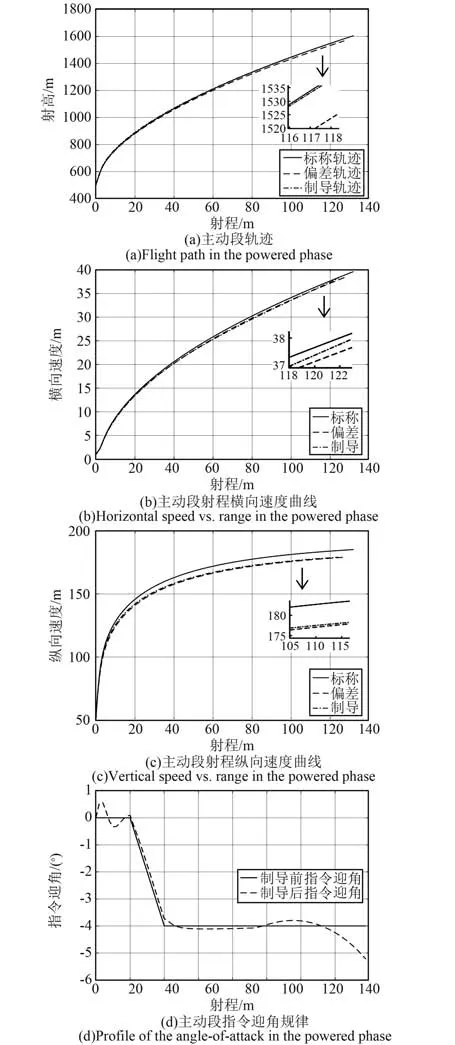
图6 LQR制导前后对比Fig.6 Comparison before and after LQR guidance

LQR制导前后对比如图6所示，仿真结果表明，在存在参数偏差情况下，实际的射高、横向速度、纵向速度均会偏离标称值。使用LQR制导以调整指令迎角的方式，能够实现对标称弹道跟踪逼近。图6中射高、横向速度的跟踪效果良好，偏差在1 m、1 m/s以内；纵向速度跟踪效果稍差，偏差在5 m/s以内。

全段轨迹如图7所示，末态参数见表7。在20 s的飞行时间内，主动段采用LQR制导律后基本实现了对射高、横向速度、纵向速度的多变量跟踪，被动段结束时射程、射高等末态参数也满足了二次分离点指标要求。

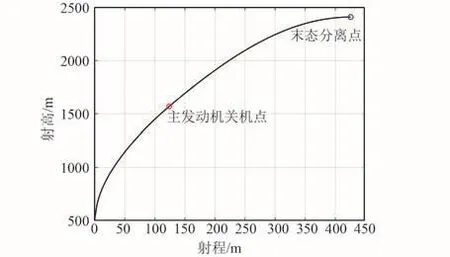
图7 飞行轨迹Fig.7 Flight trajectory

表7 全段飞行仿真结果Table 7 Simulation result of the full flight

5 结论

本文针对逃逸飞行器展开了在分离点约束条件下的轨迹设计与制导方法研究。区别于一般弹箭，逃逸飞行器只能在主动段短时间内实施制导指令，这就对标称轨迹在偏差作用下的鲁棒性提出了一定要求。主要结论如下：

1)基于误差线性化模型，推导建立了误差传播模型和LQR制导模型。相较于传统的解析法，采用误差传播法，在快速性上有着巨大的优势，通过具体算例的仿真验证了这一算法的准确性；

2)基于LQR设计了逃逸火箭的制导模型，实现了多变量跟踪，通过仿真验证了方法的可行性。

3)依据以上2种模型，详细介绍了一种可行逃逸飞行器轨迹的设计方法，在考虑偏差情况下，仍尽可能满足末态二次分离点指标，具一定有鲁棒性。