追根溯源:促进学生高阶思维能力提升的应然之道


陈惠芳,江苏省小学数学特级教师。苏州市“姑苏教育”领军人才,张家港市“陈惠芳名师工作室”领衔人,张家港市梁丰小学副校长,曾获首届“智慧·互动·成长”全国青年教师风采展示一等奖。在《人民教育》等省级以上期刊发表文章500多篇,出版个人专著《触摸教育的风景》《追寻数学生态课堂》。
导 读:
所谓高阶思维,是指发生在较高认知水平层次上的心智活动或认知能力。它在教学目标分类中表现为分析、综合、评价和创造。高阶思维是高阶能力的核心,主要是指创新能力、问题求解能力、决策力和批判性思维能力。高阶思维能力集中体现了数学学科素养的新要求,是适应知识时代发展的关键能力。发展数学高阶思维能力是课堂教学的应然追求!
高阶思维是指发生在较高认知水平层次上的心智活动或认知能力。数学高阶思维能力是近年来小学数学教师积极探讨的一个热门话题。《义务教育数学课程标准(2011年版)》在“课程目标”中明确指出:要体会知识之间、数学与其他学科之间、数学与生活之间的联系,运用数学的思维方式进行思考,增强发现问题和提出问题的能力、分析和解决问题的能力。而培育学生的高阶思维能力,对于学科素养的提升,对于学科关键能力的提高,无疑起到了一定的促进作用。
一、关注“种子课”——提高高阶思维能力的前提条件
有关专家指出:概念形成的一个主要方面是由思维的许多变式组成的,称之为复合思维,学生不仅通过自己的主观印象还可以通过存在于这些物体之间的关联把零散物体聚合起来,这样的复合思维是学生理解概念的重要基础,也是促进高阶思维能力发展的前提条件。比如:在数学学习中有一些“种子课”,“种子课”就是可供迁移、可供生长的关键课(特级教师俞正强语),可以更好地帮助学生把零散的知识聚合起来,再发散开来。在低年级教学“除法”这一内容时,很多教师往往只停留在除法上,没有很好地打通除法与其他相关知识、相关要素之间的关系。实际上,在教学这部分内容时,我们可以围绕除法的意义——一种是等分除,一种是包含除,结合除法各部分的名称——被除数、除数和商,除法算式的写法——横式和竖式,建立各要素之间的联系。
由这一节“种子课”延伸开去,到了中年级,学生先根据乘法算式(其逆运算是除法算式),如:3×4=12,来认识3和4都是12的因数,12是3和4的倍数。接着,教师可以出示一些除法算式:16÷4=4,同样让学生来判断谁是谁的因数,谁是谁的倍数?再引出质因数、分解质因数、公因数、最大公因数、公倍数、最小公倍数等一系列概念。
再到高年级,教学分数时,教师慢慢渗透“分一分,再数一数”,就得到分数,进而学习比的意义。之后,教师自然要引导学生沟通比、分数、除法之间的联系。并利用概念间的这些联系,来理解商不变的规律、分数的基本性质、比的基本性质等核心概念间的联系,从而更好地解决较复杂的数学实际问题。
由此看来,在小学阶段,像“除法”“认识厘米”“时、分的认识”等这一些种子课的教学,是后续诸多概念教学的基础,尤显重要。在进行教学设计时,教师一定要基于学情,追本溯源,关注学生的知识储备,重视引导学生由类概念引出子概念,由核心概念引出一般概念,由已知引出未知,根据学生已有的数学知识、数学活动经验,问题解决经验等来进一步掌握新的知识,洞悉新概念的意义内涵、整体结构及其背后的数学思想方法,把若干知识碎片铺展成知识的结构体系。唯其这样,才能促进学生自主构建概念,发展高阶思维能力。
二、深度研究——提升高阶思维能力的有效路径
苏州大学付亦宁博士认为:深度学习是以内在学习需求为动力,以理解性学习为基础,运用高阶思维批判性地学习新的思想和事实,能够在知识之间进行整体性联通,将它们融入原有的认知体系进行建构;能够在不同的情境中创造性地解决问题;能够运用元认知策略对学习进行调控,并达到专家学习程度的学习。
例如,江苏省常熟市石梅小学魏芳老师在执教“和与积的奇偶性”一课时,组织学生先学研究,学生通过写一些等式,列举出不同的例子,然后展示交流,观察比较,初步有了“奇数+奇数=偶数,偶数+偶数=偶数,奇数+偶数=奇数”等一些猜想。即使全班学生都得出了这样的结论,教师还是坚持追问:为什么呢?这样的结论一定是对的吗?你有办法验证吗?于是,学生一个个开始画图、交流……展示出不同的验证想法,由加法联想到乘法的意义。
教师顺学而导,渐渐帮助学生建立模型:通过下图的演示,学生明白了“奇数+奇数=偶数,偶数+偶数=偶数,奇数+偶数=奇数”的道理。
与传统的课堂教学相比,魏老师设计此环节的精妙之处,就在于引导学生进行深度研究,促进学生元认知体验。她不满足于学生的猜想,不满足于全班同学异口同声的结论。学生先学,教师依学而教,以问题为导学,组织学生深度探究,让他们验证自己的猜想,每个学生都经历了这个说理的过程,由数字到图,由图想数字所表示的实际意义,每个学生都在体验、理解、反思中学习,有效地实现了数学知识向学科关键能力的转化,较好地培育了学生的学科素养。
课尾,教师再次让学生自我回顾梳理:刚才我们是怎么探索规律的?由于有图文对照,学生借助图形,再次由问题引发猜想,举例验证,说理证明,得出结论,运用结论去发现问题……
由此可见,数学是思维的体操,数学教学中,教师引导学生抓住概念本质,聚焦“和与积的奇偶性”内核要素的分析,通过说理、举例,让学生真正亲历“究竟是奇数还是偶数”这个结论的形成过程,促进学生的数学思考,形成学生深度的认知状态,从而揭示出概念内涵——“和与积的奇偶性”的实质。真正用数学的方法来发现问题,探索规律,从而培育学生的观察比较、理性思考、批判性思维能力等学习品质,提升高阶思维能力。
三、自我迭代——延展高阶思维能力的基本要义
迭代,是指利用变量的原值推算出变量的一个新值。在这里,特指学生在一定的学习活动情景下,通过教师的引导,在遇到新问题时,能自觉唤醒经验,能主动追本溯源,联想到已有的知识和经验,尝试解决问题,发展思維能力。
在教學苏教版小学数学四年级“用画图的策略解决实际问题”单元复习课时,教师先让学生回顾本单元的知识点,然后说说自己有什么困惑,或者可以进行推荐“好题分享”活动,自觉建构新知识,生成一种面积模型,形成富有个性的问题解决方案,积累问题解决经验。以下是课堂教学片段:
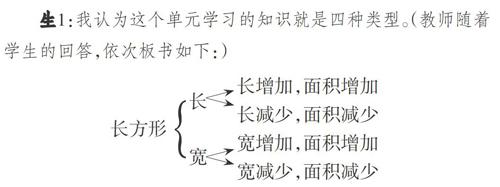
生1:我认为这个单元学习的知识就是四种类型。(教师随着学生的回答,依次板书如下:)
[长增加,面积增加
长减少,面积减少
宽增加,面积增加
宽减少,面积减少
][长方形][长][宽]
生2:我补充,虽然你说了四种类型,但是问题不一样,有时求现在的面积,有时求原来的面积。
生3:有时还要求减少或增加的面积。
师:其他同学有补充吗?
生4:除了长方形的面积,我们还学了正方形面积的变化。
师:好的,我们先来复习长方形面积变化这一类题。昨天有同学进行了好题推荐,先看这两题:
(1)有一块长方形花圃,长8米,在修建校园时,花圃的长增加了3米,这样面积增加了18平方米,求原来花圃的面积是多少平方米?
(2)东山小学有一块长10米的长方形花圃,在修建校园时,花圃的长减少了2米,这样花圃的面积就减少了12平方米,现在花圃的面积是多少平方米?
学生交流后,教师指名学生展示求解过程,并分析数量关系,比较两个题目的异同。
学生很快找到了两个题目的相同点:都是长方形,都是长在发生变化,根据长的变化和对应面积的变化,先求出宽。不同点是:第一题是求原来的面积,第二题是求现在的面积。
师:老师为大家鼓掌!但我们的研究不能止步于此,由这两个题目你还想到哪一类题型?
生5:有时候题目里告诉我们,长方形的宽发生了变化,可能宽增加,也可能宽减少,面积发生变化。
师:那你觉得,要求的问题可能是什么?
生6:可能是求原来的面积,也可能是求现在的面积。
师:很好!由这个长方形你还想到哪个图形面积变化?
生7: 正方形面积变化。
师:如果是正方形,它的边长会怎么变化?
生7:如果是正方形,它的一组边长都增加,或者都减少。我们做过课本上第53页的第7题。
师:你的记忆力真好!这一类题目大家能总结一下方法吗?
生8:根据边长增加面积增加,求出原来的边长,再求出原来的面积。根据边长减少面积减少,求出原来的边长……
师:刚才同学们从长方形长与宽的变化、面积的变化,想到了正方形边长的变化、面积的变化,大家觉得还有哪一类知识不太明白?
生9:有关小路的面积,还有铺地砖的问题,我不太会解决这类问题。
师:正好作业单上有这道题:“在一个边长是8米的正方形草坪四周有一条1米宽的花圃。在花圃里栽牡丹花,每棵占地1平方米,一共要栽多少棵?”大家试试自己解决问题。
学生独立思考后,教师投影一个学生作业,并请他讲讲解决问题的过程。
生1:我是这样想的,要回答一共栽多少棵,先要知道小路的面积。我先算大正方形的边长:8+1+1=10(米)。
用10×10-8×8=36(平方米),求出小路的面积。
再用36÷1=36(棵),求出要栽的棵数。
师:大家有什么问题吗?
生2:为什么要用8+1+1,草坪外面有一条1米宽的花圃,我觉得应该是8+1=9(米)?
……
师:大家回忆一下,通过今天的单元复习,你有什么体会和收获?
生3:画图可以帮助我们分析数量关系,找到解题的方法。
生4:解决面积这一类的题目,都是用长×宽或者边长×边长的面积公式。
生5:复杂的题目,其实都是简单题目拼起来的。
……
师:同学们,大家说得都很有道理。解决“长方形、正方形这一类面积变化的题目”,其实都用到了最基本的数量关系式:长×宽=面积,或者边长×边长=面积。其他的都是根据这一组公式延伸而来的。所以到中高年级,等我们学习三角形、平行四边形、梯形等面积公式时,还是要运用今天的知识。长方形的面积、正方形的面积是所有图形面积计算公式中的基础。
从上面的教学片段我们不难看出,在教学中,教师没有一味地依照自己的设想,机械地读背面积计算公式,大量做题,巩固知识,而是让学生先自我梳理与回顾,以自主探究为主线,以典型题型为依托,从最基本的长方形面积计算入手,丰富问题背景,触类旁通,举一反三。在关键处给予引导,在疑虑处给予点拨,让学生主动去追本溯源,架构核心知识的认知结构,逐步形成数学的思维方式和理性的数学精神。
基于上面的思考,我以为,学生高阶思维能力的培养不是一蹴而就的。教师无为,学生才能无不为!只有让学生追本溯源,经历从现象到问题,从问题到操作,从操作到思考,从结果到过程的嬗变,经历身、心、灵的内化,学生才能用数学的眼光去观察这个世界,享受到探究数学知识的乐趣,发展数学思维,真正提高学科关键能力,提升高阶思维能力。
(作者单位:江苏省张家港市梁丰小学)
□责任编辑 周瑜芽
E-mail:jxjyzyy@163.com

