从两则案例谈“基本活动经验”教学

申一健

摘 要：《普通高中数学课程标准（2017年版）》已于2018年1月正式公布，其中提到在教学中，教师应根据相应教学内容落实“四基”，培养“四能”，促进学生核心素养的形成与发展，其中“四基”指“基本知识、基本技能、基本思想、基本活动经验”。文章通过两个案例谈谈如何落实“基本活动经验”教学，促进学生相关核心素养的培养与发展。

关键词：教学案例;基本活动经验;数学教学

中图分类号：G633.5 文献标识码：A 收稿日期：2019-05-19 文章编号：1674-120X（2019）30-0077-02

一、“四基”与课堂教学的理解与认识

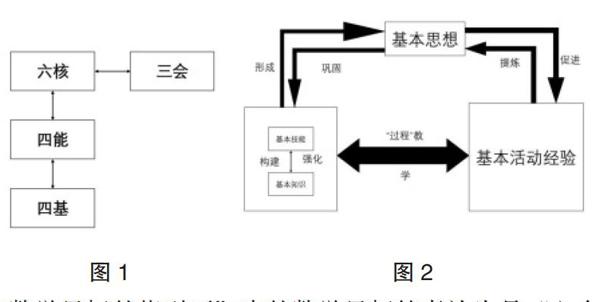
《普通高中數学课程标准（2017年版）》（以下简称新课标）提出“四个基本”“四种能力”“六个数学核心素养”“三个会用”的内容，这里简称“四基”“四能”“六核”“三会”（下同）。这四个内容是一个整体，需从系统的角度来理解与认识。它们的关系如图1所示。

不难看出，“四基”与“四能”是“六核”的下级目标，是“六核”的细化与分解。“六核”的培养须通过“四基”与“四能”来体现。落实对“四基”与“四能”的培养与形成需借助课堂教学。

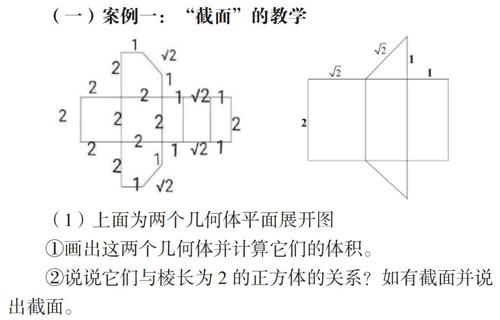
“四基”与“四能”的培养将成为数学课程课堂教学的教学目标。“四基”中的基本知识与基本技能是大家熟知的教学目标，基本思想是老问题新内涵。新课标实验版提到，基本思想与方法是新课标（实验阶段）的三维目标之一。新课标所提的基本思想的内涵较之前有传承，更有升华。正如文中所说，上位“基本思想”指归纳与演绎，是希望学生领会以后能够终身受益的那种思想方法，要与换元法、待定系数法、配方法等数学方法区别开来。基本活动经验是全新的教学目标，是一线数学教师的一个陌生概念，也是新课标数学课程的重点之处。这“四种基本”的内在联系如何？许多专家与一线老师已有阐述，笔者认为它们关系如图2所示。

张奠宙教授对基本活动经验定义为：在数学目标的指引下， 通过对具体事物进行实际操作、考察和思考， 从感性向理性飞跃时所形成的认识。数学活动经验的积累过程是学生主动探索的过程。定义中的“具体事物”笔者认为就是数学问题，即带有问题情境、含有探索过程的学习问题;而“进行实际操作、考察和思考”笔者认为就是分析、讨论、求解;“在数学目标的指引下”中的数学目标笔者认为是“六个核心素养”。基本活动经验可以理解为，课堂教学中，构建实验问题，通过对问题的分析、讨论、求解的学习，获得从感性向理性飞跃时所形成的认识和对“六核”的培养。毋庸讳言，基本活动经验必须通过课堂教学的活动来完成与形成。课堂中怎样的教学活动才是基本活动经验所具备的活动？

二、由案例说“基本活动经验”教学

（一）案例一：“截面”的教学

（1）上面为两个几何体平面展开图

①画出这两个几何体并计算它们的体积。

②说说它们与棱长为2的正方体的关系？如有截面并说出截面。

（2）一种元器件为直四棱柱ABCD-A'B'C'D'（ 侧棱垂直底面），AB=AD=A A'=2BC=4，AD∥BC。P为矩形D D'C'C内一点，现在过P与棱B B'的截面上植入电子芯片。

①画出过P与棱B B'的截面并说明作图的理由。

②试讨论芯片的尺寸大小。 （结论不唯一，合理即可）

本案例两个问题都是以“截面”为中心构建的立体几何问题，它们在题设与设问上采用更富有探索性的实验过程设计。张奠宙教授就数学活动经验的特征指出：“数学活动经验， 是具有数学目标的主动学习的结果。数学经验来源于日常生活经验， 却高于日常经验。”这说明落实“基本活动经验”课堂教学过程具有数学性。这种数学性特征之一为：课堂教学的教学活动具有探讨、分析、求解等环节，把知识传授与获取数学学习经验充分结合。不难看出，本案例的问题（1）通过以二个几何体平面展开图为载体，分析、讨论几何体的切割与组合，在实验过程中探索几何体中截面的形成，获得认识截面的经验。这一教学过程需要直观想象、运用逻辑思维及几何计算。这种数学性另一特征体现在教学内容要有数学性。一般情况下，课堂教学内容依据的是教材的内容，而教材内容是课堂教学的蓝本。有经验的一线教师根据所教学生的实际情况往往会对内容进行二次加工。在这一过程中不能忽略内容的数学性。此外，在“基本活动经验”课堂教学中引进与改编一些教学材料时要注重数学性。本案例问题（2）是根据高中数学必修2（人教版）P59例3改编过来的，较原题在设问上更具开放性，较问题1在对“截面”认识上更上一层楼。问题（2）的第②问要讨论芯片的尺寸必须计算截面的尺寸，包括长、宽与周长、面积。所以芯片的尺寸在截面范围内都可以，而形状不限。该问题本质是强化对“截面”的认识。

（二）案例二：“对称”教学

地图上有城市A，B，它们在河h的同一侧但不在河沿上（河h可视为直线）。现某规划设计人员只有一把尺子，计划在河沿上找一处建立货物中转站P，使城市A、B与P的距离和最短。

（1）若以河h为x轴，如何在直角坐标系中将上述问题表述出来？

（2）写出该规划人员的操作与计算过程。（该人员在地图上测出长度可设为a、b、c等小写字母。地图长度单位为cm，实际距离单位为km）

（3）说说：P是以A、B为焦点，椭圆与直线h的位置关系？

“基本活动经验”教学的课堂结构如何？简单地说怎样的课才符合“基本活动经验”的教学要求？史宁中教授所阐述的是，新课标之前教学大纲强调数学课堂教学目标的二维性即基本知识与基本技能，课堂教学活动围绕知识的传授、应用与技能（运算与证明）的熟练来展开。新标准数学课程实验阶段，教学目标增加了数学思想与方法，形成了目前每节数学课三维标准，旨在加强对学生能力的培养。新课标重在提倡对学生智慧的培养。笔者认为一个人对某一件事行为能力达到创新与变革的时候便可以称之为智慧。史教授在文中又指出，智慧不是表现在经验与思考的结果上，而是表现在经验与思考的过程中。这说明知识结论的运用不能产生智慧，也不能有效培养智慧。课堂教学中，应有目的地设计教学过程，在过程的活动中获得经验，形成归纳的数学思想，锻炼创新意识。本问题3个设问层层递进，通过对实际问题建模递进式进行试验探索，找到P点的位置。层次1即设问（1），P点为x轴上与A、B距离和最小的点。这一设问另一功能是锻炼学生用数学语言表达世界的素养。层次2即设问（2），由对称知识已知P是A 关于x轴对称点A'与B连线A'B与x轴的交点（将A换成B也可）。层次3即设问（3），以（2）中P得到|PA|+|PB|为长轴长，|AB|为焦距椭圆M，在直角坐标系作平行x轴的直线l，直线l与椭圆M相切时切点为P（此时l与x轴重合）。这样的教学过程浸透对“学生智慧的培养”，会有效提高其学科素养。

所以，“基本活动经验”的教学就是针对性强且富有数学实验过程的教学。“基本活动经验”教学的结构是带有数学实验过程的过程教学。

三、“基本活动经验”教学标准探讨

前面已经提到“四基”“四能”是“六核”的细化与具体体现。 落实“基本活动经验”的教学要有对“六核”培养的具体指向与具体措施。案例一教学可培养学生数学抽象、直观想象、数学运算等方面的核心素养;案例二教学可培养学生数学抽象、数学建模、数学运算等方面的核心素养，还可以培养学生用数学语言来表达实际问题的能力。

情境材料要具有时效性与实用性。前面已经论述了“基本活动经验”教学是具有数学实验特征的过程教学，情景材料必不可少。笔者认为材料应来源于生活但必须高于生活;材料也要适合学生，不能把高中课堂材料放到初中教学。 此外，所选材料还要与学生“知识与技能”相匹配。

四、结语

过程教学目标要明确，方式要灵活。“基本活动经验”教学中，教学活动一定要有经验的获得，这些经验可以是某一个结论、构建的模型、有实用价值的结果等，这些经验对学生后续学习有启迪作用。“基本活动经验”教学中，教学活动应充分与现代信息技术融合，利用图形计算器、建立数学实验室都是行之有效的方式方法，能极大地增强教学效果。

参考文献：

[1]中华人民共和国教育部.普通高中数学课程标准（2017年版）[M].北京：北京人民教育出版社，2018.

[2]史宁中.《数学课程标准》的若干思考[J].数学通报，2007，46（5）：1-5.

[3]黄加卫.摭谈“数学基本活动经验”及其案例研究[J].中学数学杂志（高中版），2009（4）：6-8.