唯一可着色图研究进展

(兰州大学 信息科学与工程学院， 甘肃 兰州 730000)

1 引言及预备知识

设G=(V,E)是一个无向简单图.图G的一个k-着色是指从G的顶点集V到颜色集 {1,2,…,k}的映射c，满足对任意的uv∈E，有c(u)≠c(v). 图G是k-可着色的，如果G有一个k-着色.图G的色数，记作(G)，是指使得G为k-可着色的最小正整数k.若(G)=k，则称G是k-色图.显然，图G的每个k-着色c可以看作是对顶点集V的一个划分 {V1,V2,…,Vk}，其中，Vi表示分配到颜色i的所有顶点构成的集合，i=1,2,…,k. 称集合Vi为着色c的色类.易验证，每个Vi是图G的独立集.

图G的两个k-着色c与c′称为是等价的，如果由这两种着色导出的V的无序划分是相同的.图G称为唯一k-可着色的，如果(G)=k，且G的任意两个k-着色是等价的. 也就是说，在不考虑颜色置换的情况下，G只有一个k-着色.可看出，唯一k-可着色图G的所有k-着色导出的V的无序划分是相同的.例如，完全图Kn是唯一n-可着色图.

此外，唯一可着色图可根据其色多项式来定义.设P(G,x)为图G的色多项式，则G是唯一k-可着色图当且仅当P(G,k)=k!，关于图的色多项式的研究可参见文献[1-3].

图的唯一可着色问题最早是由Chartwright等[4]在研究符号图的着色时提出的(符号图唯一可着色的研究可参见文献[5]).随后，一般图的唯一可着色问题[6]以及平面图的唯一可着色问题[7]都有了研究.

图的唯一可着色问题与经典的图着色问题研究的侧重点有所不同.经典的图着色问题主要在刻画给定图的色数，而唯一可着色问题主要判断哪些图是唯一可着色的.

根据唯一可着色的定义，知道并不是所有的图是唯一可着色的.1980 年，Dailey[8]证明了对任意图G，判断G是否为唯一可着色图的问题是NP-完全的.因此，关于唯一可着色图的研究主要集中在结构特征、存在性以及构造等方面.

本文主要介绍唯一可着色图研究的重要结论，特别是唯一3-可着色平面图的相关结果.文中未给出的定义及符号，请参照文献[9].

2 唯一可着色图的性质

1968年，Chartwrigh等[4]初步刻画了唯一可着色图的特征，得到如下定理：

定理2.1[4]若G是一个唯一k-可着色图，则在G的每个k-着色下，G中任意两个色类导出的子图是连通的.

1969年，Harary等[6]进一步得到了唯一k-可着色图G的一些基本性质如下.

定理2.2[6]若G是唯一k-可着色图，则：

(1)G的每个同态像也是唯一可着色的；

(2)若对G添加一个新顶点w，使得w与G的除一个外的每个色类中的至少一个顶点相邻，则所得到的图是唯一k-可着色的；

(3)若u是G中的一个度为k-1的顶点，则G-u也是唯一可着色的.

定理2.1是唯一可着色图的一个简单但非常重要的结论.由定理2.1，容易得到下面的推论.

推论2.1设G是一个n-阶唯一k-可着色图，则G至少含有e*(G)条边，其中，

由于(k-1)-树是唯一k-可着色图，且阶数为n的(k-1)-树恰含e*(G)条边，因此推论2.1中的下界是可以取到的.一个图G称为k-树，如果G要么是k+1个顶点的完全图，要么在G中存在一个顶点u，使得u的邻域是一个包含k个顶点的团，且G-u仍是k-树.

1981年，Truszczyński[10]研究了恰含e*(G) 条边的n-阶唯一k-可着色图的性质.另外，记r(k)为团数是k-1的唯一k-可着色图的最小的阶数，Truszczyński证明了定理2.3.

定理2.3[10]r(3)=12，r(4)=10，且对任意的k≥5，r(k)=k+5.

2000年，Daneshgar等[11]通过引入唯一k-可着色图的核的概念，推广了 Truszczyński[10]得到的若干结果.唯一k-可着色图G的核是指G中的一个导出子图H，满足H不含G的规模为1的色类中的顶点，也不含G的度数为k-1的顶点.Daneshgar等[11]证明了对任意的k≥3，不存在边数极小的(k,2k)-核，但对任意的k≥4，存在边数极小的(k,2k+1)-核，其中(k,n)-核是指n-阶唯一k-可着色的核.

1990年，Xu[12]猜想如果G是一个阶数为n，规模为e*(G)的唯一k-可着色图，则G包含同构于完全图Kk的子图.然而，在2001年，Akbari等[13]发现了一个阶数为24的不含三角形的唯一3-可着色图其边数为45. 该结果否定了Xu[12]的猜想.更一般地，他们证明了对任意k≥3，存在边数为e*(G)的不含Kk的唯一k-可着色图.

1973年，Wang等[14]得到了不含三角形的唯一k-可着色图顶点数的一个下界.

定理2.4[14]对任意k≥3，若唯一k-可着色图G不含三角形，则G的顶点数严格大于k2+k-1.

1978年，Bollobás[15]得到了一个图G是唯一k-可着色的两个充分条件.

定理2.5[15]设G是一个n-阶k-可着色图，其中k≥2.

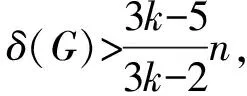
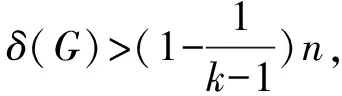
1983 年，Tucker[16]通过引入图的顺序着色，研究了完美图的唯一可着色问题.一个图G称为完美图，如果对G的任意一个导出子图H，有(H)=ω(H)成立，其中ω(H)是指H的团数，即H的最大团的顶点数.Tucker[16]证明了对于两类完美图G，G是顺序k-可着色的当且仅当它是唯一k-可着色的.图G称为可比较图，如果存在G的一个定向，使得其相邻关系满足传递性.图G称为弦图，如果G的每个长度大于等于4的圈均包含弦.

定理2.6[16]若G或G的补图是可比较图或弦图，则G是顺序k-可着色的当且仅当它是唯一k-可着色的.

另外，Tucker[16]提出如下猜想：

猜想2.1[16]设G是完美图，则G是顺序k-可着色的当且仅当它是唯一k-可着色的.

关于完美图的唯一可着色的研究可参见文献[17-18]，以及关于强完美图猜想的综述[19].

1998 年，Mahmoodian[20]引入了图着色的定义集来研究唯一可着色图.图G着色的定义集是指G的一个带有颜色的顶点子集S，满足S的着色能唯一地扩展为G的一个(G)-着色.

1999年，Hajiabolhassan等[21]证明了如下定理：

定理2.7[21]图G是唯一可着色的当且仅当G的任意着色c:V(G)→{1,2,…,(G)}的所有极小定义集恰包含(G)-1个顶点.

2003 年，Daneshgar等[22]进一步讨论了与图的唯一可着色和定义集相关的若干参数.

2008 年，Hillar等[23]利用代数的方法刻画了唯一可着色图的性质，并给出了判断一个图是否唯一可着色的算法，利用该算法，他们验证了Akbari等[13]给出的关于Xu[12]的猜想反例.

3 唯一可着色图的存在性和构造

关于围长较大的唯一k-可着色图的研究主要分为存在性和构造两个方面.事实上，多数有关存在性的证明都采用的是构造的方法.

1969年，Harary等[6]首先构造了一个不含三角形的唯一3-可着色图F(如图1所示)，并通过F与完全图Kk-3的联运算，得到如下结论：

定理3.1[6]对所有的k≥3，存在一个不含Kk的唯一k-可着色图.

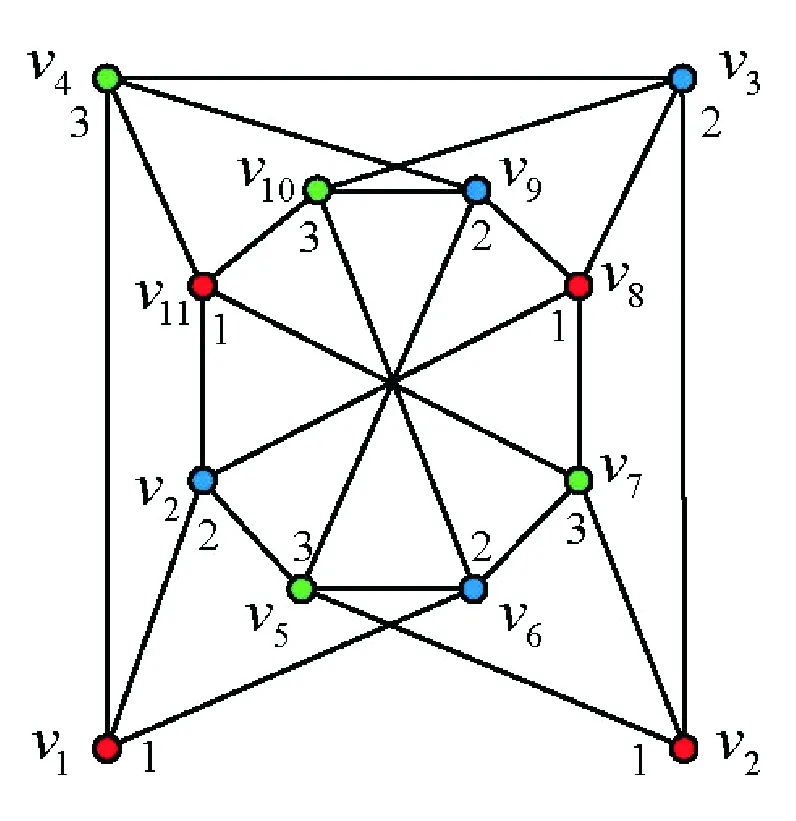
图1 一个不含三角形的唯一3-可着色图FFig.1 An uniquely 3-colorable graph F without triangles

注：在Harary等[6]的文章中，构造的图F存在错误，没有将边v1v4,v2v3连接.

定理3.2[26]对任意的k≥1，存在不含三角形的唯一k-可着色图.

1974年，Greenwell等[27]考虑了存在不含短奇圈的情况.

定理3.3[27]对任意的k≥3和给定的s，存在唯一k-可着色图，其不含长度小于等于s的奇圈.

1975年，Müller[28]解决了此问题的一般情形(也见文献[25])，即证明了定理3.4.

定理3.4[28]对任意的正整数k(≥3)和t，存在唯一k-可着色图，其不含长度小于等于t的圈.

其中Müller采用的也是构造的方法.1976年，Bollobás等[29]给出了一种非构造性的方法，即概率方法证明了此结论.

1998年，Emden-Weinert等[30]也利用概率方法，得到了一个带有顶点数和最大度条件限制的结论.

定理3.5[30]对任意给定的正整数k和g，存在围长至少为g的唯一k-可着色图，满足其顶点数不超过k12(g+1)，最大度不超过5k13.

两个图G和H的弱积，记为G×H，其顶点集为V(G×H)=V(G)×V(H)，边{(u,v),(u′,v′)} ∈E(G×H)当且仅当uu′∈E(G)且vv′∈E(H).

Greenwell等[27]在研究不含短奇圈的唯一k-可着色图的存在性时，主要利用了唯一可着色图与完全图的弱积图的唯一可着色性的关系.他们证明了若H是连通图且(H)≥n+1，则H和完全图Kn的弱积图H×Kn是唯一n-可着色的.1985 年，Duffus等[31]进一步研究了弱积图的唯一可着色性质，证明了若G和H都是包含Kk的唯一k-可着色图，则G×H也是唯一k-可着色的.特别，对图1所示的F以及任意4-色图H，F×H是唯一3-可着色的.

1974 年，Osterweil[32]通过引入6-团环构造了一类唯一3-可着色图，并说明可通过6-团环构造其它的唯一3-可着色图类以及唯一k-可着色图类，其中k≥3.

1996 年，Chia[33]结合图的自同构群方法，将Osterweil[32]给出的构造唯一3-可着色图的方法推广到了唯一k-可着色图上，其中k>3.

1974 年，Nieminen[34]构造了一类非唯一k-可着色图G，满足在G的任意k-着色下的q个色类导出的子图是唯一q-可着色的，其中q≤k-1，k≥3.

1993年，Chao等[35]通过构造的方法证明了存在一类不含三角形的唯一3-可着色的正则图，这类图含有(24)2k个顶点，每个顶点的度数均为k+5；从而得到如下定理:

定理3.6[35]对任意正整数k≥3，存在一类不含Kk的唯一k-可着色正则图.

进一步，在1998年Chao等[36]也通过构造的方法证明了定理3.7.

定理3.7[36]对任意的正整数n与r≥5，存在一类含(26)n·2r-5个顶点的r-正则唯一3-可着色图.

1997年，Daneshgar[37](也见文献[38])引入了强迫技术来研究唯一可着色图的构造.对任意的正整数t和充分大的正整数k，Daneshgar利用强迫技术，构造了团数为k-t的唯一k-可着色图，并分析了所构造图G的参数Λ(G)=|E(G)|-e*(G)的若干性质.

2007 年，Zhao等[39]利用递归的方法，构造了一类顶点数为n，边数为e*(G)，且最小度为k的唯一k-可着色图.

2016年，笔者等[40]给出了3种递归构造唯一3-可着色图的方法，可通过阶数较小的唯一3-可着色图构造阶数较大的唯一3-可着色图.并且，给出了Xu[12]猜想的一个简单反例G16，如图2所示.此图是不含三角形的唯一3-可着色图，其顶点数为16，边数为29.

图2 唯一3-可着色图 G16Fig.2 An uniquely 3-colorable graph G16

在图G16的基础上，笔者构造了一类4-正则且不含三角形的唯一3-可着色图.结合定理3.7可得到定理3.8：

定理3.8[40]对任意正整数r≥4，存在一类r-正则唯一3-可着色图.

4 唯一可着色平面图

1969年，Chartrand等[7]开始对平面图的唯一可着色问题展开研究.唯一1-可着色平面图是平凡的，即只有K1. 容易证明，唯一2-可着色平面图只有连通的平面二部图.对于更一般的情况，他们证明了定理4.1.

定理4.1[7](1)至少含4个顶点的唯一3-可着色平面图至少包含2个三角形；

(2)唯一4-可着色平面图是极大平面图；

(3)不存在唯一5-可着色的平面图.

特别，设G是一个色数为3的平面图.如果G包含三角形T，使得对G中任意顶点v有一个三角形序列T,T1,T2,…,Tm，序列中相继的三角形有一条公共边，而v在Tm中，则G是唯一3-可着色的.

对唯一4-可着色平面图，有下面的猜想：

猜想4.1[41]若极大平面图G是唯一4-可着色的，则G是递归极大平面图.其中G称为递归极大平面图，如果G可在K4的基础上通过不断地在某个3-度面上嵌入3-度顶点得到.

猜想4.1也被称为唯一4-可着色平面图猜想，该猜想最初是以边着色的形式提出的.因为一个给定的平面图与其对偶图是相互对应的，故平面图的点着色、面着色以及边着色在一定条件下可以相互转化.

1973 年，Greenwell等[42]首先研究了图的唯一边着色问题.Fiorini等[43]，及Fisk[44]于1977年分别提出了下述猜想：

猜想4.2[43-44]每个至少有4个顶点的唯一3-边可着色立方平面图包含三角形.

根据一个平面图与其对偶图的结构特征，易证明猜想4.1与猜想4.2是等价的.1988年， Hind[45]证明了猜想4.2的极小反例不含长为4的圈.1996年，Goldwasser等[46]证明了猜想4.2的极小反例是循环5-边连通的.1998年，Fowler[47]在其博士论文中利用类似于证明四色定理的方法给出了猜想4.1的一个证明，但该证明未见正式发表.

1977年，Aksionov[48]改进了唯一3-可着色平面图中三角形数的下界，并且，详细刻画了恰含3个三角形的唯一3-可着色平面图的结构特征.

定理4.2[48]阶数大于等于6的唯一3-可着色平面图G至少包含3个三角形.并且，若G恰含3个三角形，则：

(1)G中的3个三角形依次相邻；

(2)G的所有面部圈中除3个3-圈，1个5-圈以外，其余面部圈均为4-圈；

(3)G的面部5-圈的边界上存在一个2-度顶点.

2017年，笔者等[49]对恰含4个三角形的唯一3-可着色平面图的结构特征进行了刻画，得到以下定理4.3.

定理4.3[49]若阶数大于等于6的唯一3-可着色平面图G恰含4个三角形，则 0≤|E(G)|-2|V(G)|+3≤1，且：

(1)当|E(G)|-2|V(G)|+3=1时，对任意的i≥5，G中不存在i-度面；

(2)当|E(G)|-2|V(G)|+3=0时，F5+(G) 中只包含两个5-度面或一个6-度面，其中F5+(G) 表示G中所有度数大于等于5的面构成的集合.

设G是一个唯一k-可着色图，如果对任意的边e∈E(G)，都有G-e不是唯一k-可着色的，则G称为边临界的.记size(n)为n个顶点的边临界唯一3-可着色平面图的边数的最小上界.

Aksionov 在文献[48]中猜想：size(n)= 2n-3且每个唯一3-可着色平面图包含相邻三角形.

然而，在同一年，Mel’nikov等[50]构造了一个反例G(如图3所示)，图G包含16个顶点和30条边且不含相邻三角形，从而否定了 Aksionov 提出的猜想.

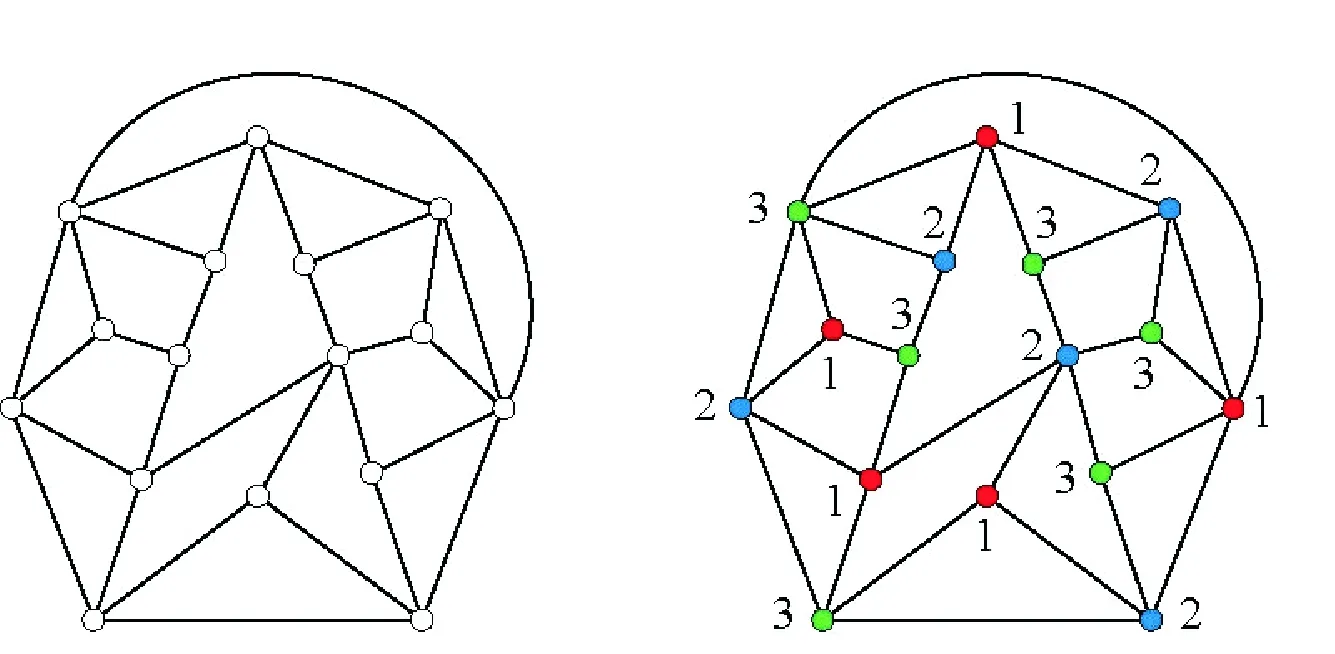
图3 Mel’nikov等猜想的反例及其3-着色

Fig.3 A counterexample of the Mel’nikov and Steinberg’s conjecture and its 3-coloring

对唯一3-可着色平面图中是否存在相邻三角形的问题，笔者等[49]给出了下面的结论：

定理4.4[49]若唯一3-可着色平面图G中的三角形数不超过4，则G包含相邻三角形.

并且，对任意大于等于5的整数k，构造了唯一3-可着色平面图G，满足G包含k个三角形，但不含相邻三角形 (如图4 所示).

此外，Mel’nikov等证明了图3所示的平面图G是边临界的.将G复制多次，并将其粘连起来，也就是说，使得这些图依次有一条公共边，这样可得到一类边临界唯一3-可着色平面图.基于此，Mel’nikov等提出了下面的问题：

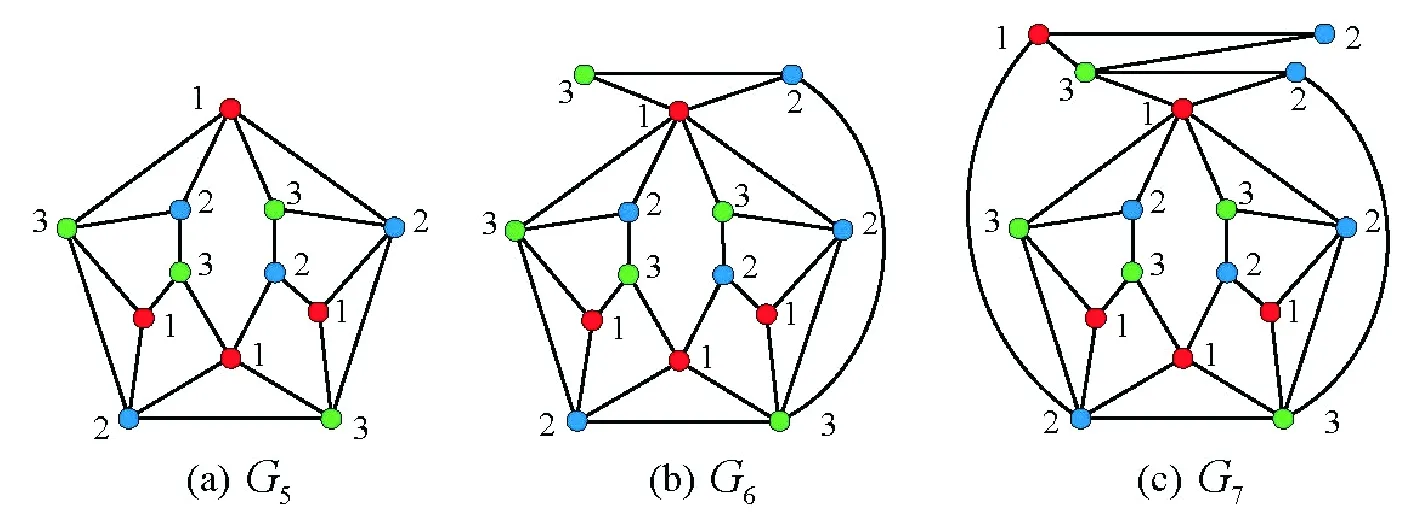
图4 不含相邻三角形的唯一3-可着色平面图构造

Fig.4 Construction of uniquely 3-colorable planar graphs without adjacent triangles

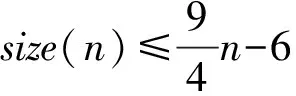
问题4.2[50]是否存在整数n0，使得若一个平面图G中的任意两个三角形的距离大于等于n0，则G不是唯一3-可着色的? 有可能n0=1.

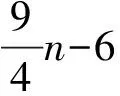
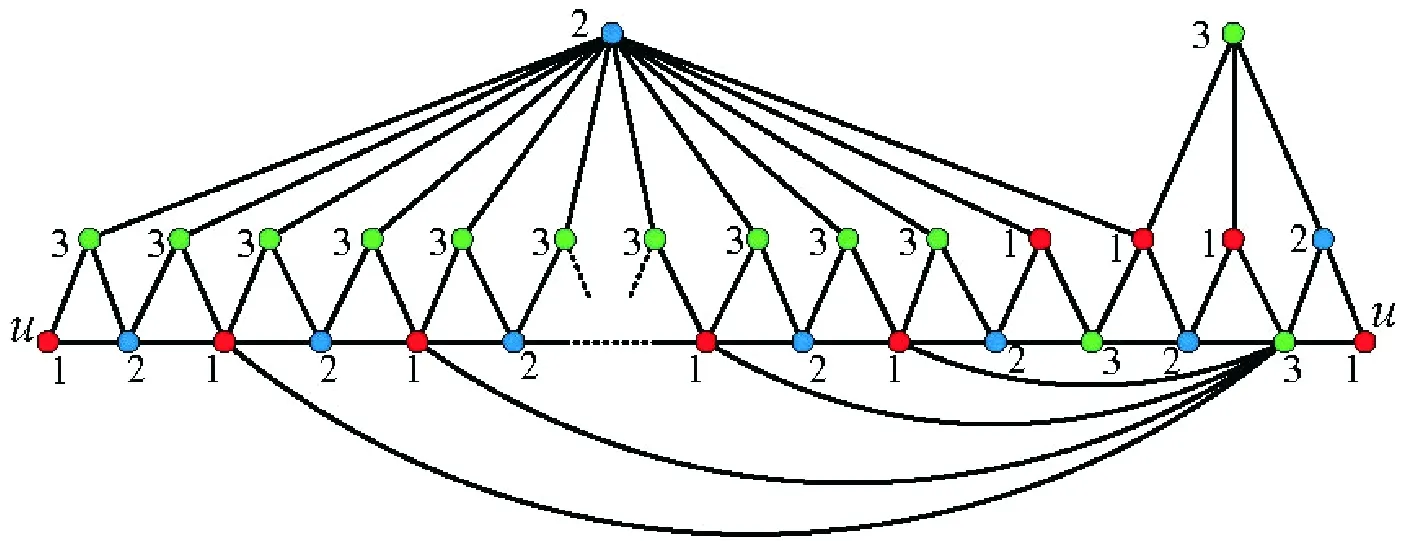
图5 Matsumoto 构造的边临界唯一3-可着色平面图

Fig.5 The edge-critical uniquely 3-colorable planar graph constructed by Matsumoto

另外，Matsumoto 引入了Δ-面圈的概念.对一个平面图G，G中的一个Δ-面圈C=T1T2…Tk是指G的由k个三角形Ti的顶点和边构成的子图，其中Ti与Ti+1有一条公共边，i=1,2,…,k，且Tk+1=T1. 例如，图6所示的图是一个Δ-面圈.

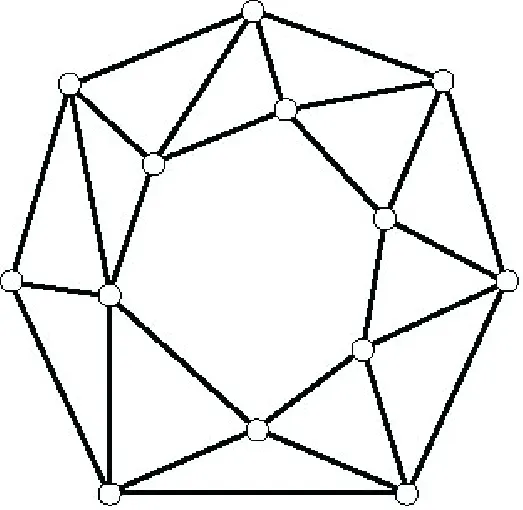
图6 一个Δ-面圈Fig.6 A Δ-face cycle

通过证明边临界唯一3-可着色平面图不含Δ-面圈，Matsumoto 得到定理4.5.

笔者通过分析唯一3-可着色平面图中Tri-子图的性质，改进了Matsumoto 得到的关于size(n)的上界.设G是唯一3-可着色平面图，H是由三角形序列T1,T2,…,Tt构成的G的子图，且对每个Tj，存在i∈{1,2,…,j-1}使得Tj与Ti有公共边，其中j=2,3,…,t，则称H为G的Tri-子图.G的一个Tri-子图称为极大的，如果G中不存在Tri-子图H′，使得H⊆H′.

定理4.6[52]设G是一个唯一3-可着色平面图且G不含分离3-圈，G0是G的一个唯一3-可着色子图，且H1,H2分别是G的两个极Tri-子图.若E(G0)∩E(Hi)=∅, 其中i=1,2, 则有

(1)G0和Hi至多有一个公共顶点，其中i=1,2；

(2)对任意的i∈{1,2}，有e(V(G0),V(Hi))≤3，特别，若G0和Hi有一个公共顶点v, 则e(V(G0-v),V(Hi-v))≤1；

(3)若H1与H2有一个公共顶点v,G0与Hi有一个公共顶点vi且v≠vi, 其中i=1,2, 则G0,H1与H2的并是唯一3-可着色的.

进一步，引入并分析了唯一3-可着色平面图的Tri-特征图的结构特征(详细定义参见文献[52])，在此基础上证明了定理4.7.

另外，笔者证明了定理4.8.

定理4.8[53]任意唯一3-可着色平面图包含一个3-度面与一个k-度面相邻，其中3≤k≤5；进一步，采用构造的方法，证明了存在唯一3-可着色平面图，其中每个3-度面既不与i-度面相邻，也不与j-度面相邻，其中i,j∈{3,4,5} 且i≠j.

同时，提出如下猜想：

猜想4.3[53]设G是3-连通唯一3-可着色平面图，则G中存在3-度面与k-度面相邻，其中3≤k≤4.

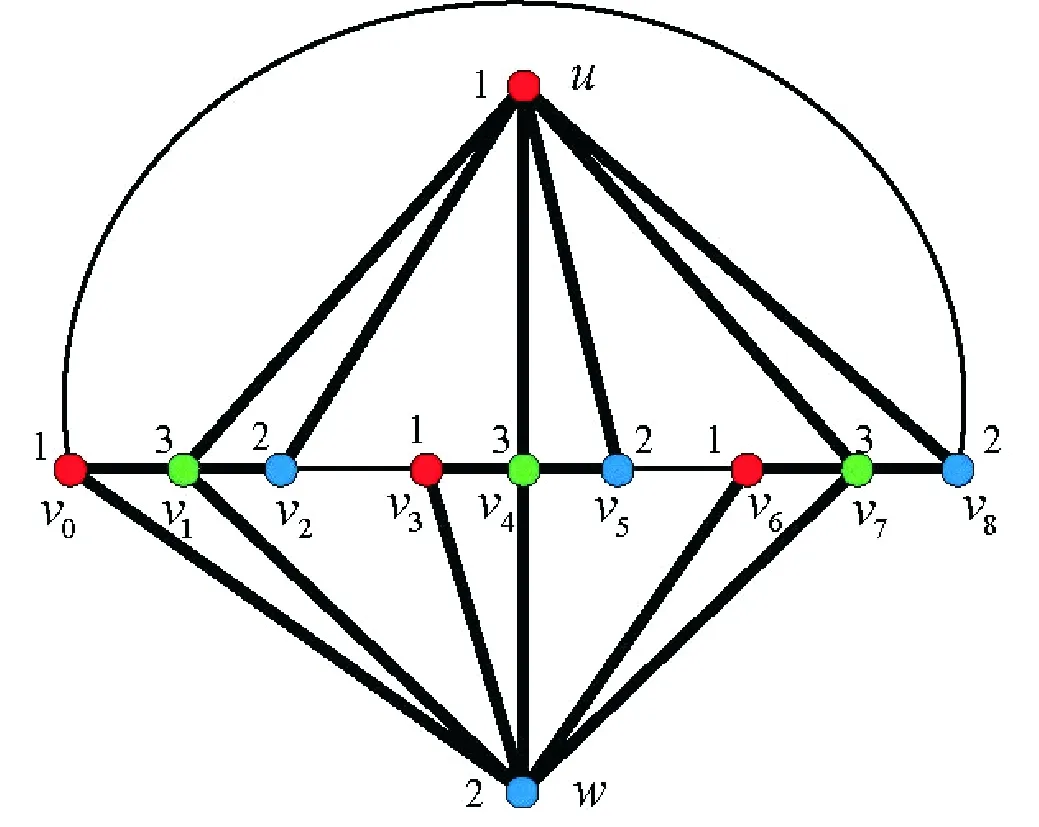
图7 不包含相邻3-度面与3-度面、相邻3-度面与5-度面的唯一3-可着色平面图

Fig.7 An uniquely 3-colorable planar graph with neither adjacent 3-face and 3-face nor adjacent 3-face and 5-face

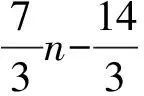
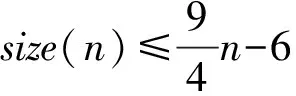
推论4.1[53]任意满足n≥11和n≡2(mod 3)的奇数n，有

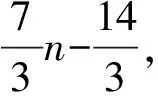
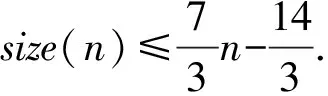
猜想4.5设G是一个唯一3-可着色平面图，则G中存在两个含有公共顶点的三角形.

5 结论与相关研究

本文对唯一可着色图，特别是唯一3-可着色平面图的相关研究结果进行了综述，主要从结构性质、存在性、构造等方面对其展开介绍，并总结了一些目前尚未解决的问题.

类似于唯一可着色图，唯一边可着色图和唯一全可着色图的问题也被相继提出并进行研究.

图G的一个k-边着色是指从E到颜色集 {1,2,…,k}的映射f，满足对任意的xy∈E，有f(x)≠f(y).图G的边色数，记作′(G)，是指使得G有k-边着色的最小正整数k.图G称为唯一边可着色的，如果E可以被唯一地划分为′(G)个色类.关于唯一边可着色图，有下面重要结论：

定理5.1[54]对任意k≥4，唯一k-边可着色图只有星K1,k.

定理5.1最初是Wilson 于 1967年提出的猜想，被Thomason 于 1978年给出了证明.当k=1或k=2时，判断唯一k-边可着色图的问题是平凡的.当k=3时，有许多相关研究结果和未解决的问题[42,54-57].

猜想5.1[55]设G是一个唯一3-边可着色简单立方图，则G包含Petersen-子式或三角形.

猜想5.2[56]设G是一个唯一3-边可着色简单立方图，则G包含snark-子式或三角形.

图G的一个k-全着色[58]是指从V∪E到颜色集{1,2,…,k}的映射f，满足对任意的相邻或关联元素x,y∈V∪E，有f(x)≠f(y)，其中顶点u与边e关联是指u是e的一个端点.图G的全色数，记作″(G)，是指使得G有k-全着色的最小正整数k.图G称为唯一全可着色的，如果V∪E可以被唯一地划分为″(G)个色类.例如，路和长为n(n≡0mod3)的圈是唯一全可着色图.1995年，Mahmoodian等[59]提出了如下猜想：

猜想5.3[59]除空图、路和长为n(n≡0mod3)的圈之外，再没有唯一全可着色图.

1997年和2003年，Akbari 等[60-61]得到了唯一全可着色图的若干性质，并证明了一些图类不是唯一全可着色的，部分肯定了猜想5.3.