带有阻尼项小周期椭圆边值问题的高阶三尺度渐近分析

周文利, 冯永平

(广州大学 数学与信息科学学院, 广东 广州 510006)

随着数值分析方面计算机软件和硬件发展, 出现了许多涉及具体物理和工程问题的计算方法. 但对于具有小周期微观结构问题的计算, 用有限元方法求解时, 由于复合材料的不均匀性, 需要非常精细地划分有限元网格, 这就导致了最后在求解线性方程组时的巨大计算量, 即使是大型甚至是超级计算机也无法完成对应的计算工作. 针对这类问题, 多尺度方法和均匀化方法发展了起来， 首先, 文献[1]给出了均匀化理论并构造了椭圆型方程双尺度的渐近展开式，文献[2]对小周期椭圆混合边值问题作了双尺度有限元分析. 然后, 文献[3]研究了二阶椭圆边值问题的特征值和特征函数的双尺度渐近展开, 并给出数值算法. 还有一些文献用双尺度方法研究了小周期椭圆问题, 如文献 [4-6]. 此外, 用双尺度方法还可以解决具有小周期结构的热弹性耦合问题, 文献[7]创新性地建立了这个问题中位移场和温度场的双尺度渐近展开式.

由于某些材料或问题具有多尺度特性, 用双尺度方法处理这些问题时会有一定的局限性, 因此，非常有必要在双尺度方法的基础上发展三尺度方法. 通过三尺度方法, 文献[8]预测了纤维混凝土的力学性能, 文献[9]讨论了材料的热传导性能. 随后, 文献[10]在三尺度展开的基础上加入高阶校正项, 即用高阶三尺度方法分析了复合材料的力学性能.

本文用文献[10]中的思想方法在三个不同尺度上分析带有阻尼项小周期椭圆边值问题解的高阶三尺度渐近展开. 微结构层次下包括两种不同的单胞, 分别是带有微观尺度ε2的微观单胞ε2Z和带有介观尺度ε1的介观单胞ε1Y, 其中ε2≪ε1≪1. 带有阻尼项的椭圆第一边值问题为

(1)

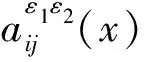
设x表示Ω中的宏观尺度坐标系,y表示ε1Y中的介观尺度坐标系,z表示ε2Z中的微观尺度坐标系,它们之间有如下关系：

(2)

定义关于x的微分算子

(3)

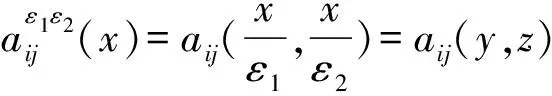
由于系数的多尺度性, 问题(1)的解析解一般得不到. 用常规的数值方法计算时需要对网格做精细剖分, 运算量非常大. 易证明问题(1)存在唯一解, 本文主要讨论问题(1)的形式三尺度解.

1 uε1ε2(x)的高阶三尺度渐近展开

为使文章简洁和运算方便, 引入下面的记号

D1=Dx,x,D2=Dx,y+Dy,x,D3=Dy,y,

D4=Dx,z+Dz,x,D5=Dy,z+Dz,y,D6=Dz,z

(4)

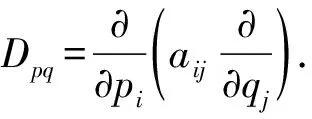
由式(1)和(3),

duε1ε2

(5)

基于已知结果[11]和复杂的求导过程, 经过不断的校正分析, 可以建立uε1ε2(x)的高阶三尺度渐近展开式, 即

(6)

其中

(7)

这里的u0(x)只反映问题(1)解的宏观性质, 并称之为定义在Ω上问题(1)解的均匀化解.Bp(y)、Bpq(y)、Hs(z)、Hst(y,z)、Gs(y,z)、Hspq(y,z)、Hstpq(y,z)、Kp(y,z)、Mst(y,z)和Np(y,z)是定义在单胞Y、Z上的函数, 称为单胞函数.

把式(6)代入式(5), 整理, 则有

ε1(D1uI+D2uII+D4uIV+D5uVI+D6uVII+duI)+

O(ε2)=-f

(8)

由于系数ε1和ε2是任意的, 所以得到下面一串等式:

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

D6uV+du0=0

(17)

(18)

ε1:D1uI+D2uII+D4uIV+D5uVI+D6uVII+duI=0

(19)

(20)

(21)

(22)

(23)

下面将对式(9)～(23)逐一分析以确定均匀化问题和单胞函数所满足的单胞问题. 由于u0(x)不依赖于y和z,uI(x,y)和uII(x,y)不依赖于z, 根据式(4)可知式(9)～(13)成立.

由式(14)、(7)和(4), 可得

(24)

又由式(15)、(7)和(4), 可得

从式(24)可知上述等式成立.

再由式(16)、(7)和(4), 可得

(25)

定义与微观尺度邻域Z相关的体积平均算子

(26)

把体积平均算子(26)作用到式(25)的两边, 根据Green公式, 则有

(27)

其中

(28)

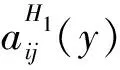
(29)

类似地, 由式(17)、(7)和(4), 可得

ψ1=-f-du0

(30)

其中

(31)

把体积平均算子(26)作用到式(30)的两边, 利用Green公式, 则有

-f-dZu0

(32)

再定义与介观尺度邻域Y相关的体积平均算子

(33)

并把体积平均算子(33)作用到式(32)的两边, 根据Green公式, 可以得到宏观尺度上的均匀化方程

(34)

其中

(35)

(36)

(37)

根据式(32)和(34), 可得

(38)

于是可以定义Bpq(y)满足的单胞问题

(39)

此外, 把式(32)代入式(30), 可得

(40)

其中

根据式(29)、(37)和(39)可知ψ2与ψ3不等于零, 为使式(40)保持等号成立, 可以构造Gs(y,z),Hst(y,z)满足的单胞问题分别是

(41)

(42)

由式(18)、(7)和(4), 可得

(43)

从式(24)可知上述等式成立.

类似于上面的分析和运算, 从式(19)～(23)、(7)和(4), 可以定义Hspq(y,z),Hstpq(y,z),Kp(y,z),Mst(y,z)和Np(y,z)满足的单胞问题分别为

(44)

(45)

(46)

(48)

综上所述, 可以得到以下定理:

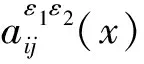
(1)问题(1)的解uε1ε2(x)具有形式渐近三尺度解(6);

(2)问题(1)解的均匀化解u0(x)由问题(37)确定;

(3)问题(1)的均匀化系数由式(28)、式(35)和式(36)确定;

(4)局部单胞函数Hs(z)、Bp(y)、Bpq(y)、Gs(y,z)、Hst(y,z)、Hspq(y,z)、Hstpq(y,z)、Kp(y,z)、Mst(y,z)和Np(y,z)分别由问题(24)、(29)、(39)、(41)、(42)、(44)～(48)确定.

在上面的讨论中, 定义了在单胞Y和Z上的单胞函数, 这些单胞函数反映了uε1ε2(x)的某种局部性质. 需要指出的是, 定义在介观单胞上的局部单胞问题附带的是周期性边界条件, 定义在微观单胞上的局部单胞问题附带的是Dirichlet边界条件.

2 uε1ε2(x)的误差分析

基于前面的讨论, 分别定义如下不同的多尺度近似解

(49)

(50)

(51)

(52)

(53)

(54)

从式(52)～(54)可知，二阶双尺度解和低阶三尺度解产生的误差较大, 高阶三尺度解产生的误差较小, 因此，寻找问题的高阶三尺度解在实际计算中是非常有必要的, 它提高了计算的准确度.

3 总 结

由于某些材料或问题具有多尺度特性, 用双尺度方法处理这些问题时会有一定的局限性, 因此，很有必要在双尺度方法的基础上发展三尺度方法以及精确度更高的高阶三尺度方法.

本文首先在高阶三尺度方法的理论框架下, 通过逐步构造和分析, 得到了带有阻尼项小周期椭圆边值问题解的三尺度渐近展开式. 在此过程中, 均匀化系数和均匀化方程通过均匀化方法来获得. 均匀化方程所确定的均匀化解对高阶三尺度近似解起决定性作用, 反映了高阶三尺度近似解的宏观性质, 而单胞函数反映的是高阶三尺度近似解的局部性质. 最后基于构造的高阶三尺度渐近展开式, 定义了二阶双尺度解、低阶三尺度解和高阶三尺度解, 分析了它们与高阶三尺度近似解之间的误差, 由此表明高阶三尺度解产生的误差较小, 为进一步建立高阶三尺度有限元数值算法提供了理论依据.