基于神经网络的主瓣干扰抑制技术
李嘉辛,王 宏,江朝抒,石林艳,廖翠平
(1.电子科技大学信息与通信工程学院,四川 成都 611731 2.中国电子科技集团公司第51研究所,上海 201802)
0 引 言
雷达干扰技术的不断发展促使雷达抗干扰技术也在逐步提升。而主瓣抗干扰也是现在研究的热门方向。可以通过空域滤波对干扰进行抑制[1],通过对接收信号进行空域加权,使得在期望接收信号无失真通过,在干扰所在角度位置形成零陷。当干扰出现在主瓣内,利用自适应波束形成的方法,会产生主瓣畸变且峰值偏移等问题,进而导致了测角误差较大,无法正确检测目标所在方位。为了解决这些问题,Yu等人提出了基于阻塞矩阵预处理的方法[2],此方法进行预处理后的信号不含主瓣干扰,因此在波束形成时在主瓣位置不会产生零陷,使得主瓣方向图保形效果较好。但是该方法无法在主瓣方向图位置形成零陷,属于接收后处理,且需要对主瓣干扰位置进行精确估计,鲁棒性较差,并且会带来主瓣峰值偏移。而J. Qian等人采用补偿方法,有效的解决了峰值偏移问题,但是依旧无法在主瓣位置形成零陷的同时,尽可能的使得主瓣具有较好的保形效果[3]。近年来,很多人采用了神经网络对权值进行学习并处理的方法[4],但是依旧无法很好地解决上述问题。在本文中,提出了一种基于神经网络的主瓣干扰抑制方法,其优点在于可以在主瓣干扰位置处形成零陷,并保证了零陷对主瓣影响尽可能的小,并且形成了较低的旁瓣电平,且无需对主瓣干扰位置进行精确估计也可以实现主瓣干扰的有效抑制,具有良好的鲁棒性。通过仿真,输入干噪比(INR)在30 dB和20 dB时,输出方向图均具有良好的效果。除主瓣干扰位置外,此方法可以得到更优的测角误差,从而实现对目标角度的精准检测。
1 信号模型
本文所提出的方法适用于具有确定阵元排布的阵列结构,例如线阵,圆阵,面阵等等。这里采用均匀线阵作为模型来分析,其他阵列分析过程类似。
接收天线由M个相同且均匀分布在直线上的全向天线阵元组成。选取第一个阵元为参考阵元,阵元编号依次为m=1,2,3,…M,阵元间距为d,λ为输入信号波长,如图1所示。

图1 均匀线阵模型
设波束指向方位角为θ0,主瓣内只存在一个干扰,且预估计主瓣干扰信号方位角为θ1。设接收信号为窄带信号,且目标与主瓣干扰信号都是远场入射,那么在该模型下,阵元接收到的干扰信号的导向矢量为:
a(θ)=[1,ej2πdsinθ/λ,ej2πdsinθ/λ,…,ej2π(M-1)dsinθ/λ]T
(1)
此方法中采用单快拍数据进行分析,则在单个快拍时刻下,天线接收到的信号可以表示为
α=Aejφφ
(2)
其中A表示为接收信号的幅度,φ为接收信号相位。
利用线阵接收信号的导向矢量,则每个天线的接收信号可以表示为
x=a(φ)α+n
(3)
其中a(φ)表示接收信号的导向矢量,φ为信号方向,n表示独立同分布加性高斯白噪声,假设干扰和噪声不相关。传统方法对接收信号进行线性加权,从而形成方向图,这里我们采用神经网络结构,使得当接收信号来源于主瓣干扰方向时,方向图形成零陷凹口,而来源于波束指向时,信号可以无失真的通过,当信号来源于旁瓣时,方向图形成较低的旁瓣电平,可以更好的对目标信号进行检测。
2 基于神经网络的波束形成
2.1 BP神经网络模型
BP神经网络由三部分构成,包括输入层,隐含层,输出层如图2所示。BP神经网络的隐含层包括多层神经元,而且输入层与隐含层神经元之间有权值连接[5-6]。

图2 BP神经网络结构
隐含层可以选择不同的激活函数,来实现整个神经网络模型的构建,本文选择tan-sigmoid函数,如下式所示
(4)
输出层采用线性输出。整个训练过程可以采用不同的方法来对神经元的权值和阈值进行学习,也可以采用不同的传递函数来进行。
2.2 生成训练数据
当主瓣内只存在一个干扰时,根据式(1-3)可得,各个天线阵元接收的单个快拍信号可以表示为
x=a(φ1)α+n
(5)
此时,接收信号的干噪比可以表示为
(6)
将输入通过激活函数,即可得到该神经元的输出信号。接下来需要计算误差,而在误差计算之前,需要表示代价函数。本文采用前面介绍过的二次代价函数,其中y(x)为期望的输出值,在本文中,用ds(φ)表示期望输出,如下所示
(7)
其中w=a(φ0)·win(N),win(N)为窗函数加权,为了使得输出天线方向图旁瓣水平降低,且改善波束形成方向图的主副比。inf为接近于0的极小值,b为干扰位置理想零陷宽度,|·|为取模运算。在期望函数中,在干扰位置将会形成一定宽度的零陷,而在其他位置,保持原本方向图不变。在对期望函数构建之前,需要先对主瓣干扰进行DOA估计,从而设定零陷的位置。
2.3 实现步骤
通过对神经网络以及期望信号的构建,即可使用上面章节中的方法,采用误差反向传播算法,对神经网络中的权值进行训练确定。本文提出的方法具体实现过程如下,设阵列模型为均匀线阵,且阵元个数为M,波束指向φ0度,主瓣干扰DOA估计为φ1度,设定INR后,根据(2)、(3)式建立输入信号模型。为了实现全方位训练,输入的训练样本信号来波方向在一点角度范围内均匀选取P个样本点,为了对输出信号相位随机性进行训练,对每个来波方向样本,根据式(5)选取Q个样本,使得Q个样本相位关系服从[0,2π]的均匀分布,则可以得到P×Q个样本。对于每个输入训练样本,通过式(7)确定与之一一对应的期望信号,并将输入训练样本与输出期望样本数据归一化,从而形成神经网络可用输入输出数据。
总体步骤如下:
(1)确定天线接收阵列模型。
(2)确定波束指向角度和主瓣干扰DOA估计角度。
(3)根据信号模型分析,得到如数训练样本和期望信号样本。
(4)选择合适的神经网络模型,并进行训练,训练结束,即可使用神经网络结构进行数据处理
3 仿真分析
3.1 波束形成
设天线接收模型为均匀线阵,且阵元个数为17,阵元间距d=λ/2。设波束指向φ0=0°,主瓣干扰DOA估计角度为φ1=2°,输入信号信噪比依次为30 dB、20 dB,噪声为高斯白噪声。为了更好的观察主瓣,输入训练样本选取[-20°,20°]范围作为信号来波方向,且选取步进长度为0.01°,共4000个数据。对于每一个来波方向,生成100个数据,相位服从[0,2π]的均匀分布,则总共生成4000×100个训练样本。对于每个输入数据,根据式(2-4)确定对应的期望信号,窗函数选择切比雪夫窗,极小值设为1×10-8,干扰位置的理想零陷宽度设为1°。由此可构成4000×100个期望样本。若在每个方向上选取1个相位样本数据,即可得到如图3所示理想方向图。
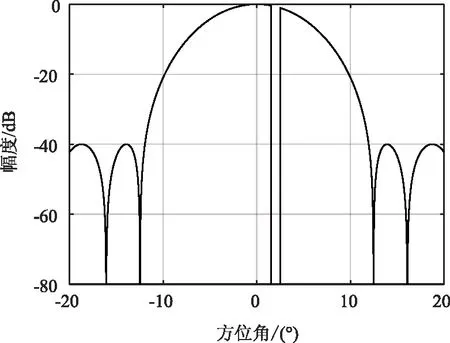
图3 理想神经网络
当确定输入信号与期望函数后,需要确定神经网络中神经元的个数。神经元个数并不是越多越好,神经元较多时,将会使得计算时间很长,甚至会引起过拟合等问题,本文采用2层隐含层,第一层神经元个数为100,第二层神经元个数为40。通过神经网络逐步学习,当误差达到设定值或者误差不再减小的时候,确定该网络结构已经被训练完成。利用训练好的神经网络进行测试可得最终输出方向图,如图4所示。

图4 不同干噪比下BP神经网络波束形成
由图4(a)~(b)可以依次给出了当干噪比INR依次为30 dB、20 dB时的神经网络输出方向图。为了对比神经网络方向图的形成效果,图4给出了接收信号中主瓣内没有干扰时的波束形成。
从图4可以看出,当干扰信号强度较强时,输出方向图的神经网络学习效果较好,能够在主瓣干扰位置形成较深且凹口较窄的零陷。同时,对主瓣其他方位影响较小,且能够形成较低的旁瓣电平。而随着干扰强度的下降,噪声将会对整个系统产生较大的影响,从而不利于干扰的有效抑制。但是与不存在干扰的接收信号相比,此方法能够对干扰进行一定效果的抑制,且在其他方向有较为良好的幅度响应。
为了更好的体现本文方法的实用性和有效性,本文将通过测角来进一步验证。下面将利用和差波束比幅测角的方法进行测角分析,在下面小节中将分别介绍和差波束形成以及由S曲线得到的测角结果。
3.2 和差波束
当利用神经网络进行波束形成后,即可将处理后的数据进行测角分析,而在本文中采用单脉冲比幅测角的方法进行[9-10]。此方法较为传统,原理在本文中将不再详细描述。仿真中采用的波束中轴线指向为0°,并形成左右两个不同方向指向的波束,波束中心指向分别为-1.5°和1.5°。对于每个波束,分别建立神经网络模型并进行训练,将得到的神经网络模型直接用于数据处理,然后将两个波束进行和差处理,将得到如图5和图6中所示的和差波束形成图。

图5 不同干噪比和波束形成

图6 不同干噪比差波束形成
由图5(a)~(b)和图6(a)~(b)可以依次看到,当干噪比INR依次为30 dB、20 dB时,和差波束形成效果有明显的变化。当干扰强度较高时,和差波束具有良好的波束形成效果。从图5中可以看出,在波束中心轴方向将形成和波束的最大指向,以及差波束的凹口。并且在和差波束中,在干扰位置形成了较为明显的凹口。但是由于噪声影响,形成的凹口内起伏较为明显。通过蒙特卡洛仿真可以进一步分析效果。
在下面小节中,将利用形成的和差波束,进行差和比S曲线的构建,通过建表,进一步实现测角。并将利用蒙特卡洛仿真分析测角效果。
3.3 测角误差
本节将详细分析测角结果。当阵列模型不变,输入干噪比依次为30 dB、20 dB时,分别形成和差波束。通过理想数据进行差和比,建立误差-角度表,然后计算不同信噪比的差和比,将得到差和比进行查表,即可得到输出误差[11-12]。通过对上面形成的和差进行比值,则可以得到如图7所示S曲线。

图7 不同干噪比下S曲线
从图7可以看出,存在干扰时的S曲线,在干扰位置处误差较大,但是在主瓣内的其他方向,与没有干扰的S曲线相比,误差较小。利用S曲线,可以将比值进行存储,即可用于对接收数据的测角分析。
为了更好地分析神经网络波束形成对主瓣干扰的抑制效果,本文中选择对主瓣方向内的接收信号进行分析,分析[-6°,6°] 范围内的测角结果。本文做了1000次蒙特卡洛仿真,得到最终测角的均方根误差,并与没有干扰的情况做了对比,如图8(a)~(b)所示。

图8 主瓣范围内测角的均方根误差
由图8可以看出,不同干噪比下,在主瓣内,除了干扰附近较窄的凹口范围内,其他方向的测角误差与没有干扰时相差不大,可以有效的测得目标角度。从而可以验证,本文所提方法,当主瓣内只存在一个干扰时,已知主瓣干扰DOA估计后,可以有效的对干扰实现抑制,从而实现对目标的有效测角。
4 结 语
本文利用神经网络,对主瓣干扰用空域的方法进行抑制。通过对信号模型的分析以及神经网络的构建,从数字波束形成的角度,在已知主瓣干扰DOA估计时,形成了较为理想的天线方向图,可以有效地在主瓣干扰位置形成零陷的同时,保证了零陷对主波束影响尽可能的小,且具有较低的旁瓣电平。由于形成的零陷凹口具有一定的宽度,所以对干扰的DOA不需要极高的精度,因此整个系统具有一定的鲁棒性。为了验证干扰抑制后对测角S型曲线影响的问题,本文实现了测角的相关仿真,可以得到在干扰抑制的同时,保证了对目标的有效测量,误差较小。

