基于离群点检测的不确定数据流聚类算法研究
叶福兰
(福州外语外贸学院,福建 福州 350202)
0 引 言
伴随信息技术快速发展,数据流模型的应用逐渐深入各个应用领域。这些领域要求数据传输速度快,且传输规模大[1]。但由于各种外界环境因素干扰,数据流出现不确定性,不确定数据流的挖掘和研究逐渐成为相关专业人员关注的重点问题。相关研究表明[2],基于离群点检测的不确定数据流聚类可检测网络恶意攻击行为,能够挖掘网络中被忽视的异常数据,为维护网络安全起到十分重要的作用。。
一些现有的研究成果,如文献[3]基于距离准则进行数据间离群点判断,提出了离群点检测DOKM算法。根据数据流概念漂移检测结果来自适应地调整滑动窗口大小,从而实现对数据流的离群点检测,结果表明,DOKM算法在人工数据集和真实数据集中均可以实现对离群点的有效检测。文献[4]提出了障碍空间中基于密度的不确定聚类算法。利用三角模糊数和R树的性质提出TF-Initialseeds算法来解决数据的不确定性问题,在基于密度聚类方法的基础上,利用Voronoi图剪枝策略可以有效减少计算量的特性。文献[5]提出了改进的DBSCAN聚类和LAOF两阶段混合数据离群点检测方法。针对DBSCAN算法中参数ε和Minpts需要人为确定而导致聚类质量差的缺点,给出了通过输入K近邻的个数代替Minpts,并通过K近邻确定聚类半径,从而减少参数输入提高聚类质量。通过改进的DBSCAN聚类算法对混合数据进行初步筛选,然后利用新构造的LAOF基于区域密度的局部异常因子计算筛选后数据对象的局部异常程度。结果显示该算法能够提高离群点检测的精度。
上述算法存在检测性能差以及聚类质量低的问题,因此,本文提出基于离群点检测的不确定数据流聚类算法,获取的全局离群点与局部离群点两种不确定数据流,采用一种不确定数据流子空间聚类算法完成聚类,以提高不确定数据流聚类效果。
1 不确定数据流聚类算法研究
本文研究的数据不确定性主要是由于数据受带宽传输、延迟和能量等制约因素引起的数据缺失,以及数据的不准确性。一些粗粒度的数据处理也考虑在内。数据的结构大多来自网络web网络,一般是基于流量特征的属性元组。
1.1 基于聚类划分的两阶段离群点检测算法
1.1.1微聚类划分算法
微聚类划分算法主要功能是获取数据集,选取数据集中微聚类间最小值,建立新聚类。详细步骤见算法1。
算法1:使用微聚类算法获取数据集的簇数量k与高质量的簇中心。
输入:数据集A={A1,A2,…,Ai,…,Am}中对象数量m。
输出:数据集中微聚类数量k与微聚类KBA1,KBA2,…,KBAi,…,KBAk中心。
第1步:将数据集A中的全部对象A1,A2,…,Am都初始化成一个相应的簇BA1,BA2,…,BAm,也称微聚类BAm;
第2步:选取2个微聚类间最小值BAi、BAj并删掉,建立新聚类BAh,原始对象并集即为该聚类里的对象,则BAh={BAi∪BAj};每个对象代表一个微聚类的初始均值,均值的计算是通过欧式距离求均值获得。
第3步:基于簇里对象的均值,将各个对象指定至最类似簇KBAk中,刷新簇均值,再次判定各个聚类中心[6];聚类中心是簇(欧式空间)的形心。
第4步:多次执行,簇均值固定后停止[7];
第5步:输出数据集里微聚类数量k与微聚类KBA1,KBA2,…,KBAi,…,KBAk中心。
1.1.2基于信息熵的微聚类过滤机制
信息熵可体现数据集状态,描述数据集中数据的不确定性,因此,本文采用信息熵描述数据集聚类中数据对象的部分情况。如果将某些数据点从数据集中剔除,数据集整体便出现不确定性或者无序性[8-9],此类数据点即为全局离群点。变量的不确定性与信息熵具有较大关联性。
根据上述算法1,将数据集A分成k个微聚类KBA={KBA1,KBA2,…,KBAi,…,KBAk},每个子集个体数量是k1,k2,…,km;对各微聚类建立一个矩形框R(存在最大个体数),将此矩形框实行网格划分,通过网格中个体分布信息,运算各个网格中个体数量krn;获取各个网格中个体占据的概率qi,便能获取各聚类的信息熵。
网格建立流程是:将m维目标空间划分为X1×X2×…×Xm网格,各个网络第j维目标宽度bj是:
(1)
式中,第j维目标宽度与目标函数值依次设成bj、Rj(x);第j维目标划分数量设成Xj;x轴决策变量设成x。为降低复杂性,将各个对象所占网格的方位用地址描述。
为降低分析复杂性,设定:
(2)
(3)
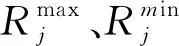

(4)
yj=mod(xj,bj)+j=1,2,…,m
(5)

存在两个目标时的目标划分示意图如图1所示。

图1 网格建立

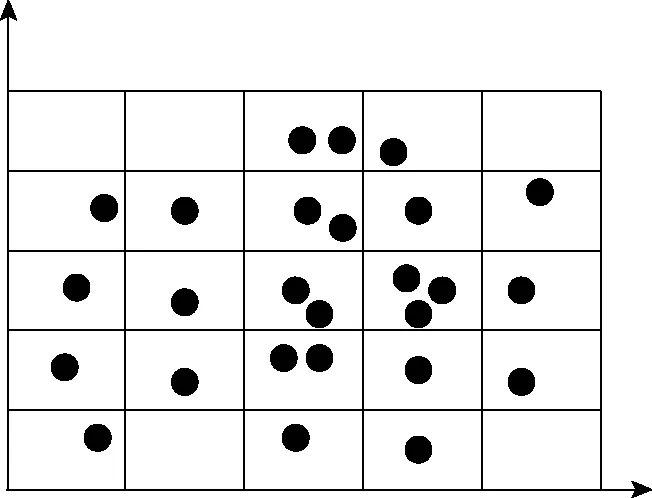
图2 数据分布
计算网格单元密度,获取各网格的数据点数量见图3。
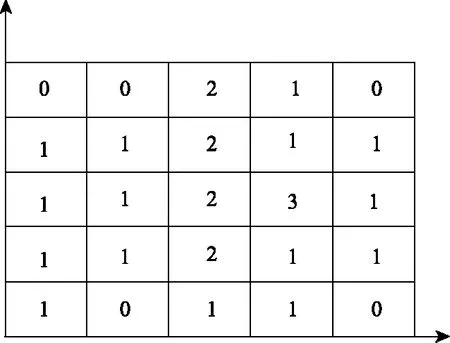
图3 网格密度
根据网格中数据的分布状态,判定个体占据的概率qi是:
(6)
根据信息熵原理建立该聚类中对象分布的信息熵D(x),信息熵变动阈值是:
β=|D(x)-D′(x)|
(7)
式中,各聚类信息熵设成D′(x);剔除偏离度最大值后微聚类的信息熵设成D(x)。对比前后信息熵的变动,设置变动的阈值为β,若β接近0,则不存在离群点,使用该种过滤方过滤掉微聚类[11];反之该对象即为离群点,把它导入离群点数据集中,该数据集称为全局离群点。
1.1.3基于距离的离群点挖掘算法
上小节获取全局离群点后,采用基于距离的离群点挖掘算法挖掘微聚类中的局部离群点[12]。基于距离的离群点挖掘算法第一步运算各微聚类中两对象间的距离,第二步总结各对象和剩余对象距离,若剔除对象后的信息熵变动大于阈值β,则该对象为离群点。
设定微聚类KBA中存在KBAj与KBAi,微聚类的对象数量设成m,n表示对象的维数(属性),KBAj与KBAi间的距离设成bij,那么KBA的聚类矩阵N是:
(8)
微聚类中第i个数据对象设成KBAi,KBAi的偏离度Eoli是:
(9)
式中,矩阵N里第i行的和等于偏离度Eoli。微聚类中各对象都具有各自偏离度Eoli,Eoli值较大,表示对象i和剩余对象聚类较远,属于异常属性的机率较大。如果k是用户期望的离群点数量,那么偏离度最大的k个对象就是局部离群点。
1.2 一种不确定数据流子空间聚类算法
基于2.1获取的全局离群点与局部离群点两种不确定数据流,采用一种不确定数据流子空间聚类算法完成不确定数据流的聚类[13-14]。将相似聚类特征的高维数据设成F,假定不确定数据流为C={vfo1,vfo2,…,vfon},其中vfoi表示随机一个不确定元组,i∈[1,n],它的概率距离特征集合是vfoi={F1,F2,…,Fn},那么对于Cq中随机两个不确定元组vfoi和vfoj间的距离近似度可根据概率距离q≤w(vfoi,vfoj,Cq)进行计算:
(10)
根据q≤w(vfoi,vfoj,Cq)计算,可将不确定元组vfo集成至非一致的Cq中,之后根据最优概率把数据流C集成不一样的簇B1,B2,…,Bm,Bi代表第i个簇。随机一个簇Bi存在多个元组,基于整体而言,元组聚集于中心点周围,能够构建新的元组。
不确定数据流子空间聚类算法必须构建NC、SW以及OC三种缓冲区。不确定数据流子空间聚类算法的聚类流程如下所示:
a:在数据流中选取n个元组设成中心点;
b:若有新元组加入SW缓冲区,SW缓冲区已满,提取SW里最老元组;
c:若OC缓冲区中存在最老元组,提取OC中最老元组,且剔除SW最老元组;
d:将新元组导至SW中;
e:BSW(SW缓冲区的簇)=Bα(新元组);
f:若返回BSW是非空状态便将新元组导至BSW中;
g:反之将新元组放置OC中;
h:若OC已满,提取OC中最老元组;
i:BOC=Bα;
j:若BOC融合了最老元组,那么将新元组导入BOC;
k:剔除OC中的最老元组;
l:引入新元组,完成聚类[15-16]。
2 实验分析
实验数据集由网络入侵检测数据集KDDUP99中获取,该数据集来源于美国空军局域网9个星期的网络连载数据。实验在数据集中的各数据中添加一个符合高斯分布的概率,让其变成不确定数据集,通过经验法则,确定聚类数据量范围为1000 GB至5000 GB。实验设置本文算法的参数为SW=200,OC=100。
实验为测试本文算法有效性,随机选取60 k的实验数据集,设定4个不同形状的聚类,原始数据集的示意图见图4。

图4 原始数据集分布
采用本文算法聚类后的效果图如图5所示。

图5 本文算法聚类结果
对比分析图4和图5可知,采用本文算法检测实验不确定数据集中的离群点聚类后,可去除原始数据集中大量离群点进行聚类,挖掘出原始数据集中4种聚类类,验证了本文算法的有效性。
采用本文算法、基于密度的聚类算法和DBSCAN聚类算法进行对比实验。
(1)离群点检测性能对比
采用三种算法簇是4和5的实验数据集中离群点进行检测,结果见表1。

表1 三种算法离群点检测性能对比结果
分析表1可知,不同簇条件下本文算法对实验数据集离群点检测的数量与实际数量最大差值为1个,其他两种算法检测的数量与实际相差较大,主要原因在于本文算法采用信息熵描述数据集聚类中数据对象的部分情况,降低了聚类分析复杂性。由此可见,本文算法检测不确定数据集中的离群点性能显著。
(2)聚类效果对比
图6是三种算法的聚类效果对比结果。

图6 三种算法聚类质量对比结果
图6(a)显示随着数据量的增多,本文算法的聚类质量大于90%,基于密度的聚类算法和DBSCAN聚类算法聚类质量都低于80%,图6(b)显示随着维度的增大,本文算法在维度值是5~23之间的聚类质量呈现上升阶段,维度值24之后聚类质量高达100%,而另外两种算法的聚类质量在维度是15之后不断降低,质量较差,说明数据集中数据维度对基于密度的聚类算法和DBSCAN聚类算法影响较大。由此可见,数据量和维度的增加未对本文算法的聚类质量产生不良干扰,本文算法聚类质量较好。主要原因在于本文算法采用基于距离的离群点挖掘算法挖掘微聚类中的局部离群点,降低异常属性的机率,提高了聚类质量。
(3)聚类算法的效率对比
图7为三种算法的聚类时间对比结果。
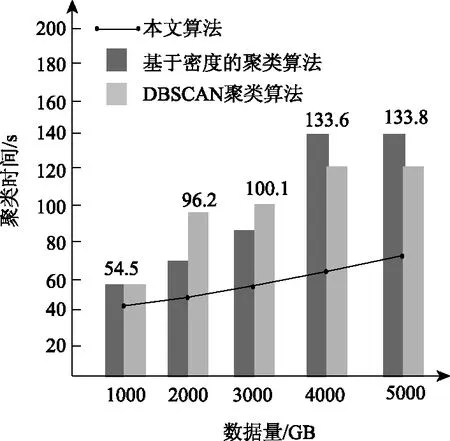
图7 三种算法的聚类时间对比结果
分析图7可知,随着数据量的增多,三种算法的聚类时间也随之增多,但本文算法耗费的时间始终低于另外两种算法,当数据量为5000 GB时,本文算法的耗时仅有75 s。
(4)聚类算法的伸缩性
图8描述三种算法的伸缩性对比结果,首先调整数据集的维度,自10变化至60,设定数据流的长度与簇数量;然后分析在数据量从1000 GB升至5000 GB时三种算法的伸缩性。
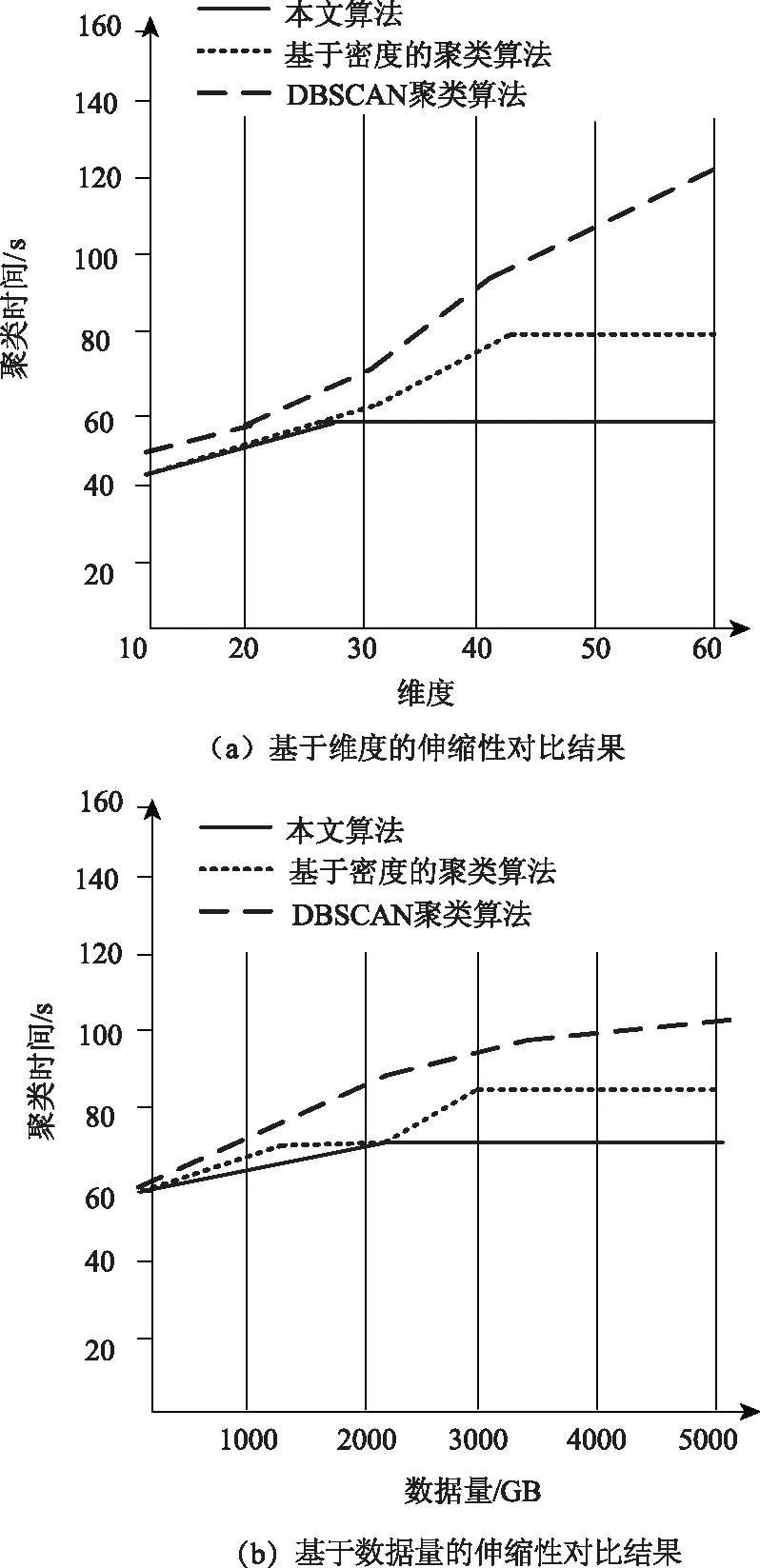
图8 三种算法伸缩性对比结果
分析图8可知,在维度与数据量逐渐增大时,本文算法的聚类时间增长斜率低于另外两种算法,由此可知,随着维度与数据量的增长,本文算法运行时间的上升速度低于另外两种算法,说明本文算法的伸缩性优于另外两种算法,不会因为维度与数量的变动产生较大的反应。
3 结 语
本文提出基于离群点检测的不确定数据流聚类算法。首先采用微聚类划分算法将数据集划分为若干个微聚类,再使用信息熵判断微聚类里是否存在离群点,如果不存在离群点,便不必进行检测,此举可减少计算量和检测误差;反之将离群点导入离群点数据集中,计算聚类里其余对象信息熵,获取全局离群点,并通过基于距离的离群点挖掘算法获取局部离群点。最终采用不确定数据流子空间聚类算法聚类不确定的数据流。本文算法与同类算法相比,离群点检测精度较高,聚类效率与聚类质量都高于同类算法,且维度与数量的变动不会对本文算法产生较大干扰。

