基于Sobel算子的双基地MIMO雷达阵列诊断方法
陈金立,卓齐刚,窦思钰,翟介新,董雨晴
(1. 南京信息工程大学气象灾害预报预警与评估协同创新中心,南京 210044;2. 南京信息工程大学,南京 210044)
0 引 言
多输入多输出(Multiple-Input Multiple-Output,MIMO)雷达是在数字阵列雷达、多基地雷达以及MIMO通信技术的基础上发展起来的一种新体制雷达[1-2]。与传统的相控阵雷达相比,MIMO雷达能灵活地根据需求设计发射波形,还可通过虚拟阵元的形成来扩展收发阵列的孔径,以提升目标可识别数目的上限,并提高目标分辨力以及参数估计性能[3-5]。天线阵列单元是雷达的关键组成部分,能够实现天线波束快速扫描、空间功率合成和多波束形成等功能,但长期工作于高频高功率下的收发组件容易损坏,从而导致相应的阵元失效。阵元失效导致其输出信号仅为热噪声,而不包含空间目标信息,从而导致MIMO雷达探测性能的明显下降。MIMO雷达探测性能的恢复需已知失效阵元的位置,因此研究有效的天线阵列诊断方法以实现失效阵元位置的高成功概率诊断具有重要的理论与实际意义[6-7]。
针对天线阵列失效单元的诊断问题,一些学者提出了一类采用波导探头测量天线阵列的远场或近场数据的阵列诊断方法。文献[8]提出了一种反向传播算法,该方法利用波导探头采样被测阵列的近场数据,再对近场数据作傅里叶变换来获得阵列的口径场分布特性,从而诊断出失效阵元的位置。文献[9]提出了一种矩阵算法,该算法首先建立探头电压与阵列激励系数的线性关系,然后利用矩阵求逆算法求解该线性关系以获得阵列激励系数,最后通过激励系数获得阵列的远场方向图从而检测出失效阵元的位置。文献[8-9]所提的阵列诊断方法要求使用探头以半波长为步进间隔采集阵列近场数据,同时要求采样数量不少于阵元数目,因此随着阵列规模的增大将导致上述方法出现采样数据大、测量时间长等问题。压缩感知 (Compressive Sensing, CS) 理论的出现为阵列诊断提供了全新的思路,该方法能够利用较少数量的采样数据检测失效阵元,逐渐成为阵列诊断领域研究的热点。文献[10]将贝叶斯压缩感知理论应用于失效阵元位置的诊断,克服了传统CS算法的测量矩阵必须满足约束等距性质的限制。文献[11]提出了一种基于lp范数最小化的均匀线阵的阵列诊断方法,能进一步地减少远场数据的采样数量。然而当失效阵元的数量较多时,失效阵元的激励系数不再满足稀疏性,导致基于CS理论的阵列诊断方法失效。波导探头的使用会增加硬件成本并干扰待测场,文献[12]直接对雷达工作期间的阵列接收数据进行差分处理来诊断失效阵元的位置,无需使用额外的波导探头,但需要遍历所有失效阵元组合情况下各差分位置上虚拟阵元的重复次数来进行失效阵元位置的搜索,且任意差分位置的虚拟阵元重复次数的错误估计均会导致阵列诊断失败,因此该方法稳定性较差,同时当阵列中的失效阵元位置使同一差分位置的虚拟阵元同时失效时,该方法无法准确诊断出失效阵元的位置。
针对上述问题及研究现状,本文提出了一种基于Sobel算子的双基地MIMO雷达阵列诊断方法,该方法利用失效阵元与正常阵元的图像边缘强度的差异特性,将失效阵元位置的诊断问题转化为图像中较低边缘强度位置的诊断问题。本文方法能够在无需使用波导探头的前提下快速有效地诊断出双基地MIMO雷达失效阵元的位置。
1 阵元失效MIMO雷达信号模型
假设双基地MIMO雷达系统由M个发射阵元和N个接收阵元组成,发射阵列和接收阵列都为均匀线性分布阵列,发射和接收阵元的间距分别为dt和dr,假设空间中存在L个远场窄带目标,第l(l=1,…,L)个目标相对于发射阵列和接收阵列的发射角(DOD)和接收角(DOA)分别为(φl,θl)。各发射阵元同时发射相同载频和带宽的周期性正交信号B=[b1,…,bM]T,bm为第m个发射阵元的发射信号,(·)T表示转置。则k时刻发射信号经L个目标反射由接收阵列接收的信号为
(1)
式中,βl为第l个目标的反射系数;ar(θl)=[1,e-j2πdrsin(θl)/λ,…,e-j2π(N-1)drsin(θl)/λ]T∈N×1为接收阵列的导向矢量;at(φl)=[1,e-j2πdtsin(φl)/λ,…,e-j2π(M-1)dtsin(φl)/λ]T∈M×1为发射阵列的导向矢量;为均值为零的高斯白噪声且与信号彼此独立。
X=AS+W
(2)
式中,A=[ar(θ1)⊗at(φ1),…,ar(θL)⊗at(φL)],⊗表示Kronecker积;S=[S(1),…,S(K)],S(k)=[s1,…,sL]T为在k时刻的目标反射系数向量;W=[w(1),…,w(K)]为高斯白噪声矩阵。
在实际应用中,随着双基地MIMO雷达天线阵列的不断增多,以及受高低温变化或振动等较恶劣的外界环境和硬件老化等因素的影响,阵列中时常会出现阵元失效的情况。定义Q为失效接收阵元的位置集合,则阵元失效双基地MIMO雷达的虚拟阵列输出信号矩阵为
(3)

其中,diag(·)表示构造对角矩阵;AT=[at(φ1),…,at(φL)]为发射阵列流形矩阵;0L×L为大小为L×L的全零矩阵。
2 常用边缘检测算子
在数字图像中,边缘是图像的一项基本特征,是指图像中局部特性的不连续导致灰度发生急剧变化的区域,边缘主要存在于目标与目标和目标与背景之间。图像边缘包含了大量的重要信息,利用图像的边缘能够描绘出目标的轮廓,因此边缘检测的研究获得了众多学者的关注。边缘检测的目的是找出图像中灰度急剧变化的区域,图像灰度的梯度能够表示图像中局部灰度的变化信息,图像中(x,y)位置上的像素的图像梯度可定义为
(4)
(1)Roberts算子
Roberts边缘检测算子利用斜向偏差分来计算梯度,其方向垂直于图像边缘,其大小代表图像边缘的强度,计算时采用对角线方向相邻两像素之差,则Roberts的梯度幅度值为:
G(i,j)=|f(i,j)-f(i+1,j+1)|+|f(i+1,j)-
f(i,j+1)|
(5)
式(5)可用卷积模板来表示
G(i,j)=|Gx|+|Gy|
(6)

(2)Sobel算子
Sobel算子是从不同的方向检测边缘,采用的是中心像素上下左右邻点灰度的加权,该算子计算边缘强度的公式表示如下:
G(i,j)=|Gx|+|Gy|
(7)

(3)Laplace算子
Laplace算子是一种二阶微分算子,对于数字图像f(x,y),Laplace算子在像素点位置(x,y)的定义为
(8)

3 基于Sobel算子的阵列诊断方法
(9)
其中,round(·)表示四舍五入取整;max(·)表示返回最大值。
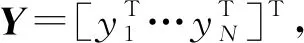
图1为双基地MIMO雷达虚拟阵列输出信号的灰度图像,其中双基地MIMO雷达的发射阵元为5个,接收阵元为15个,其中第4、6、9、14个接收阵元失效。由图1可以看出,正常接收阵元对应的图像块矩阵具有较多图像边缘,而失效阵元对应的图像块矩阵中存在较少图像边缘,因此正常接收阵元的图像边缘多于失效接收阵元的图像边缘。根据边缘检测理论可知,正常接收阵元的边缘强度高于失效接收阵元的边缘强度,因此可以将评价图像中边缘多少的边缘检测理论应用于双基地MIMO雷达的阵列诊断中。
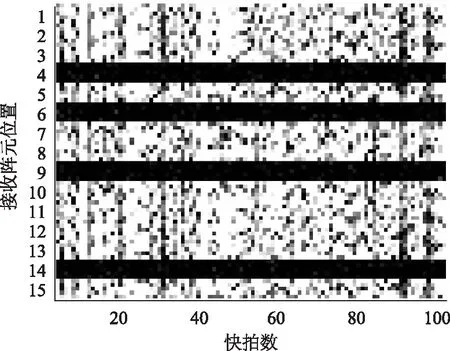
图1 虚拟阵列输出信号的灰度图像
在众多边缘检测算子中,Sobel算子在漏检边缘、假检边缘、边缘定位精度和抗图像噪声能力等方面具有明显的优势[15]。本文选取Sobel边缘检测算子计算各接收阵元对应图像块的边缘强度,由式(7)可得图像块yn,n=1,…,N中的各像素的边缘强度为
Gn(i,j)=|Gx|+|Gy|,i=1,…,M,j=1,…,K
(10)
式中,Gx和Gy分别代表经横向及纵向边缘检测的图像,(i,j)表示图像块yn中各像素的位置;Gx=yn(i-1,j+1)+2yn(i,j+1)+yn(i+1,j+1)-yn(i-1,j-1)-2yn(i,j-1)-yn(i+1,j-1);Gy=yn(i+1,j-1)+2yn(i+1,j)+yn(i+1,j+1)-yn(i-1,j-1)-2yn(i-1,j)-yn(i-1,j+1)。
根据式(10),依次对各图像块yn进行边缘强度计算,从而获得各图像块yn的边缘强度总值,即
(11)
由于失效接收阵元所对应的图像块的边缘强度较低,而正常接收阵元所对应的图像块的边缘强度较高,因此通过设定合适的边缘强度门限Gt=τ·mean(G)来诊断失效接收阵元的位置,其中τ为调节因子,mean(·)表示取均值,即
(12)
式中,Z(n)=1时表示第n个接收阵元失效,Z(n)=0时表示第n个接收阵元正常工作。
4 仿真与分析
为了验证本文方法在双基地MIMO雷达阵列诊断方面的有效性,设计了几组仿真实验,将Zhu的方法[12]和本文方法应用于阵列诊断时的性能进行对比。在以下仿真中,双基地MIMO雷达的发射阵元数M=5,接收阵元数N=15,收发阵元间距均为半波长,假设发射阵列各阵元发射相互正交的Hadamard编码信号,在每个重复周期内的相位编码个数为256。空间中存在3个远场目标,方位角度分别(20°,8°),(-10°,23°),(0°,35°),回波噪声选取均值为零的加性高斯白噪声,回波信噪比定义为
(13)
定义失效阵元诊断的成功概率为
(14)
其中,MT为蒙特卡洛实验次数;Tr为失效阵元诊断成功的次数。在本文方法中,调节因子τ=0.7。
仿真实验1:诊断成功概率随信噪比的变化关系
假设接收阵列中存在4个位置随机的阵元失效,快拍数为K=100,信噪比变化范围为-30~0 dB,进行100次蒙特卡洛实验,阵元失效的情况分为两种:(a)接收阵列中首尾阵元正常工作,每次实验的失效阵元在其余位置随机选取;(b)每次实验假设首尾阵元至少存在一个阵元发生失效。由图2(a)时的仿真结果可知,在阵列首尾处不出现阵元失效时,随着信噪比的不断增加,本文方法和Zhu的方法诊断失效阵元的成功概率均逐渐提高,但本文方法在低信噪比下仍然能准确诊断失效阵元的位置,因此其诊断性能优于Zhu的方法。由于当阵列中的失效阵元位置使同一差分位置的虚拟阵元同时失效时,Zhu的方法会因匹配搜索失败而失效,因此即使在高信噪比时Zhu的方法在个别实验中仍然会出现诊断失败的情况。由图2(b)的仿真结果可知,在阵列首尾存在失效阵元时,Zhu的方法完全失效,而本文方法依然能够准确地诊断出失效阵元的位置,因此本文方法适用于任意位置下的失效阵元诊断问题,具有良好的稳定性。

图2 诊断成功概率随信噪比的变化关系
仿真实验2: 诊断成功概率随快拍数的变化关系

图3 诊断成功概率随快拍数的变化关系
假设接收阵列中存在4个随机的阵元失效,在阵列首尾处不出现失效阵元以保证Zhu的方法工作正常,信噪比为-10 dB,令快拍数由20~100变化,进行100次蒙特卡洛实验,图3为诊断成功概率随快拍数的变化关系。由图3可知,在不同的快拍数下,Zhu的方法始终在个别实验中存在诊断失败的情况,而本文方法均能准确的诊断出失效阵元位置,无诊断失败的情况出现,因此进一步验证了本文方法的稳定性。
仿真实验3:诊断成功概率随失效接收阵元数的变化关系
为了验证本文方法在不同失效接收阵元数下的稳健性,假设接收阵列中的随机失效阵元数由1~11依次增加,在阵列首尾处不出现失效阵元以保证Zhu的方法工作正常,快拍数为K=100,信噪比为-10 dB,进行100次蒙特卡洛实验,仿真结果如图4所示。由图4可知,在失效接收阵元数不断增加时,Zhu的方法的诊断性能逐渐恶化甚至失效,而本文方法始终保持着100%的诊断成功概率,具有良好的稳健性。

图4 诊断成功概率随失效接收阵元数的变化关系
5 结 语
针对现有阵列诊断方法使用波导探头会增加硬件成本并干扰待测场等问题,本文提出了一种无需波导探头采样的双基地MIMO雷达阵列诊断方法。将双基地MIMO雷达虚拟阵列输出信号经取模处理后的数据矩阵等效为灰度图像数据矩阵,由于正常接收阵元对应的图像块中目标像素与背景像素互相重叠,而失效接收阵元对应的图像块中均为背景,因此两者的图像边缘强度存在明显差异,因此利用Sobel算子计算各接收阵元对应的图像边缘强度,从而实现双基地MIMO雷达的失效接收阵元的诊断。理论分析与仿真实验表明,本文所提阵列诊断方法在无需使用波导探头同时具有良好的诊断性能。

