机载电子“机-电-磁-气动”多场耦合系统研究方法

陈竹梅,匡云连,黄 帅,王 斌

(中国电子科学研究院，北京 100041)

0 引 言

机载电子系统加装到飞机平台上以满足装备作战功能和性能要求，在进行飞机平台加改装设计或新机型研制时，需要进行系统总体构型设计，对任务系统功能性能、载机平台气动安全性、飞机飞行性能等进行综合设计。对于预警机或特种机的构型设计来说，文献[1]提出了“基于多目标优化的总体构型设计方法”研究思路，应综合研究机载电子系统所涉及到的“机”、“电”、“磁”、“气动”等多个专业学科领域，建立平台气动特性、任务系统功能性能、结构与重量特性、载机改装及任务支持系统等之间的耦合关系及优化权衡关系[2]。分析国外一体化构型设计典型案例，多功能主动探测雷达天线、通信天线和ESM天线等，均与机体表面外形一致[3]，这种外观上呈现出“共形”，其背后的技术设计活动实质是研究解决电子学科与航空学科领域的综合与优化问题，从而实现构型一体化设计效果，以寻求最大的系统最优。目前，虽然国内外学者对多场耦合问题研究已经取得了很多成果，具有一定应用领域，如：控制系统的机电耦合、传统热结构(或流体结构)的机热耦合/机热流耦合、天线系统机电耦合/机电磁耦合等，但考虑面向预警机或特种机构型设计所涉及“机-电-磁-气动”多场耦合系统的复杂性，由于存在电子航空跨行业多学科高度交叉的现实问题，“机-电-磁-气动”复杂多场耦合系统(structural-electric-magnetism-fluid MFCS，我们也可简称为SEMF-MFCS)的多场耦合研究方法还尚存不完善[2]。本文拟探讨机载电子“机-电-磁-气动”复杂多场耦合系统，尝试提出一类复杂多场耦合系统的研究方法。

1 基于综合优化分析法的耦合问题研究

1.1 复杂多场耦合问题的收敛思路

复杂多场耦合系统的场-场耦合问题就是针对其场与场之间的关系进行综合考虑，使场与场发生作用后，还能够实现被研究对象的整体性能最优。而多场耦合分析的关键问题是研究各物理场之间耦合信息传递，也就是要合理处理各物理场之间的连续共同边界的离散。文献[4]提出，在一个二维情况下，不同物理场离散界面的网格不匹配情况，不同物理场离散边界上的信息要通过数学物理方法建立起信息传递关系。

给定初始场分布为F01、F02、…、F0n。这样，对第k个物理场，其受到其他场耦合影响后的场分布Fk为

Fk=C1kF01+C2kF02+…+CnkF0n

(1)

则所有物理场的耦合影响方程，可得到如下的矩阵表达形式

F1F2⋮Fn=C11C12…C1nC21⋮C22⋮…C2n⋮

⋮Cn1Cn2⋮CnnF01F02⋮F0n

(2)

Cij为本文定义的耦合影响算子，表示第j种物理场对第i种物理场的耦合影响。求解上述矩阵的关键是计算耦合影响算子Cij。对CijF0j而言有2种计算方法：对已经有成熟的耦合场分析方法与工具的情况采用序贯求解法，将第j种物理场的场分布F0j作为输入，加载到第i种物理场的求解器中计算；而耦合较复杂，暂时没有求解器的，可以直接使用实验数据插值或经验公式数据。由于场内部无耦合，很明显矩阵对角线上的各算子C11、C22、…、Cnn均为0。

进一步简化多场耦合模型：F=CF0。F为受到耦合影响后的统一物理场分布，F0是未考虑耦合影响的初始统一物理场分布，而C是耦合影响矩阵。由于多场耦合的存在，通常无法在一次计算后直接得到所有的耦合结果。必须进行迭代计算。令F0=F，重新计算新的动态场分布。如此经过多次迭代计算后，收敛得到的F才是接近真实场分布的场变量矩阵。

采用学科优化的方法[5]是解决这样一类大型复杂系统工程的有效方法之一。基于多学科优化的方法，对SEMF-MFCS耦合问题的求解采用综合优化分析求解方法[4]，以加快对SEMF-MFCS耦合计算的收敛速度，并且采用代理模型技术来简化和解决学科跨度较大的两两场耦合问题。

1.2 基于综合优化分析法的耦合问题求解

基于上述思路，我们可以把本研究对象所涉及到的“机-电-磁-气动”复杂多场耦合问题求解理解为是进行位移场、气动流场、磁场、电场共四个场之间的耦合分析，按照文献[4]提出的耦合理论，针对SEMF-MFCS所涉及到的“机”、“电”、“磁”、“气动”耦合问题，可以进行以下处理：

(1)鉴于SEMF-MFCS中结构与气动之间属于强耦合关系，可以建立直接的流固耦合分析，将“位移场信息”直接传递到“流固耦合界面”，“匹配到流体网络”后直接进行“流体分析”，输出“压力信息”直接传递到“匹配到结构网络”，“结构网络”输出的载荷信息传递到“结构分析”，从而建立一个闭环的“流固耦合”分析流程；

(2)鉴于SEMF-MFCS中磁场与电场之间属于强耦合关系，且均通过磁场来进行耦合表达的，因此，电场耦合问题可以处理成相对独立的节点，通过电场强度、磁感应强度信息建立与磁场之间的等效传递。如上所述，电场与磁场最后均通过结构位移传递，所以可以把气动流场与电场、磁场之间的耦合，直接处理成磁固耦合，气动流场变化通过位移来进行与磁固耦合的传递。

因此，“机-电-磁-气动”复杂多场耦合问题分析与求解示意见图1。

图1 机电磁气动耦合问题分析求解示意

2 “机-电-磁-气动”复杂多场耦合分析与优化

2.1 基于多目标函数的多场耦合优化流程

多物理场耦合问题的优化设计是建立在场耦合理论模型及其求解策略与方法基础上的。因此首先需建立基于场耦合理论模型的多学科优化模型，包括设计变量、目标函数及约束函数[6]。

如果把位移场信息作为流固耦合和磁固耦合的媒介，那么要进一步解决耦合问题的难点就在于多物理场耦合的多目标函数。构型设计多目标函数F(CFD，S)一般可以考虑四个学科方面的最具有影响性的指标特别涉及到关联因子。

针对SEMF-MFCS的“机-电-磁-气动”耦合优化，参照文献[2]提出一种多学科多物理场协同优化技术路线图，为简化追求最优过程计算的复杂程度，将不同学科求解器按照求解精度和效率进行逐步分层的解决方案，分层解决的优化设计基本流程如图2。

图2 基于多场耦合的多学科优化设计流程

这个优化流程避免了复杂多场的盲目优化，将不同学科求解器按照求解精度和效率进行分层，以期完成基于多学科分析器的高精度和低精度、长求解时间和快速求解的上下搭配。

2.2 多物理场耦合系统建模与分析

2.2.1几何建模与参数化定义

对于SEMF-MFCS中“机”、“电”、“磁”、“气动”四个物理场的耦合问题，通过上述分析，我们知道，无论是流固耦合还是磁固耦合，起核心纽带的是位移场信息。因此，研究如何提炼SEMF-MFCS几何模型的表征方法就显得十分重要，需要提取得到一种参数化的几何外形生成关系。以天线罩体为例，所需要定义几何参数化变动更改的几何控制向量X，一般是包含雷达旋罩前后位置(L)、雷达旋罩高度(H)、旋罩直径(D)、旋罩截面弧线参数({Ei})等参数变量。其中，旋罩高度(H)和前后位置参考点位置(L)就需要根据准确的几何模型设定，其示意如图3。

X=(L,H,D,{Ei})

(3)

图3 参数化旋罩几何参数示意

完成SEMF-MFCS参数化定义后，可采用CATIA、PROE等三维软件进行几何模型建模。

2.2.2气动分析与目标函数

在机载电子SEMF-MFCS中，典型的以预警机背负式天线罩为例，由于背负式天线罩不可避免地会对气动产生影响，在纵向气动特性上会产生阻力增加，纵向力矩系数变大而使得纵向静安定性增加等，在横侧气动特性上，会引起航向力矩系数巨大变化，使得飞机进入横侧不稳定，出现飘摆等现象[7]。气动分析就是需要仿真解决这些问题，主要是采用低精度高效率的面源分析方法和高精度低效率的有限体积分析代码联合仿真获得气动模块数据。面源分析方法的基本原理是通过对飞行器表面几何离散化得到的面源网格，布置偶极子和源汇模型，形成全场空间的速度场流线模型，在流线模型基础上附着物理量参数，进而获得飞行器表面的气动力参数。气动分析一般可以采取快速求解方法和高精度求解方法，以下进行方法简述。

(1)快速求解方法

流体问题求解的最终控制方程是纳维-斯托克斯方程(Navier-Stokes Equation，NSEs)，简称N-S方程。直接求解N-S方程计算量大，因此需要做出合理的简化。采用基于流线的观点描述飞行器附近主要流场的思路来进行简化，求解飞行器表面边界层外缘流场参数的问题最终可归结为求解拉普拉斯小扰动线化方程的问题。

具体而言，列写势流方法下的流动控制方程——拉普拉斯方程：

(4)

(5)

另外，运动所产生的干扰将在距离飞行器表面无穷远处衰减为0。通过施加边界条件，配平表面面源偶极子和源汇模型，可以实现将表面速度势参数线化进而形成线性代数方程组的问题转化。

(2)高精度求解方法

为了获得更加细致的流场流动信息，依然将问题从NS方程开始阐发，可以得到经典的计算流体力学方法。将NS方程的积分守恒形式写成雷诺输运定理表达形式，对于没有控制体Ω，列写输运关系为：

(6)

(7)

综合两种气动求解方法，获得参数化几何控制量和气动力系数之间的函数关系，

(8)

2.2.3结构重量分析与目标函数

结构重量分析主要依赖于三维软件包的内嵌功能，在参数化更新完成几何数据X后，可以通过脚本导出的方式获得整机的结构重量参数(包括重心位置、整机转动惯量、结构布置对整体重量提升)。形成SE2A-MFCS的结构重量参数与输入几何参数之间的目标函数。

(9)

2.2.4电性能分析与目标函数

SEMF-MFCS的电性能分析需要考虑天线性能与装载飞机平台的相互影响，如平台的散射效应、载机对天线遮挡等。因此天线布局是否合理是保证电子设备性能指标实现的关键，天线布局应不受飞机机身遮挡，或者由于机身遮挡导致的影响最小[1]。设计时首先需要解决机身对天线性能影响性分析问题，对天线遮挡效应进行仿真和评估[8]。

电大尺寸平台的存在使得电磁场包括直射场、反射场和绕射场，对个分量场叠加求和后得到总场：

E=δiEi+δrEr+δdEd

(10)

其中，Ei为直射场;Er为反射场;Ed为绕射场;δi，δr，δd为相应的计算因子。若给定天线后，电场E反映阵列天线的辐射特性，包括方向图，波瓣宽度，副瓣分布及电平，方向性系数及增益等。寻求最优的计算因子，获取最优的阵列天线辐射特性。因此，清洁区对作用距离的要求满足关系：

(11)

其中，Pav为平均功率;λ为工作波长;Gt(θ0,φ0)为天线的发射主瓣增益;Gr(θ0,φ0)为天线的接收主瓣增益；σt为目标的雷达散射截面积；k为玻尔兹曼常数，等于1.380 54×10-23W/(Hz·K)；T0为等效噪声温度，一般取为290 K；Bn为带宽；Fn为噪声系数；Ls为系统损耗；(S/C)req为检测所需最小信杂噪比。

考虑副瓣杂波对探测能力影响，天线辐射特性直接影响杂波分布，最终影响雷达的探测性能，如图4。

图4 杂波多普勒分布

雷达对天线副瓣的要求如下，θ,φ分别为俯仰角和方位角;γ为参数值;(C/N)max为最大杂噪比;(S/N)min为最小信噪比。G(θ,φ)为天线副瓣增益。

(12)

天线的性能指标的空间角度分辨率应满足下式，其中θ3为半功率波束宽度。假设均匀照射时，k=0.89。

(13)

电性能分析主要依系统最优化为思路，以满足系统作战功能及性能指标为最终目的，充分优化天线发射增益Gt(θ0,φ0)和接收增益Gr(θ0,φ0)、天线副瓣水平G(θ,φ)，半功率波束宽度θ3，形成SE2A-MFCS的电性能参数与其作战功能及性能参数的目标函数。因此，建立优化目标函数：

(R,Δθ)=(Gt(θ0,φ0),Gr(θ0,φ0),G(θ,φ),θ3)

(14)

2.2.5电磁性能分析与目标函数

SEMF-MFCS的电磁分析依照高低精度高低效率搭配的求解器选取思路，需要分别提取高低精度不同的电磁特性求解器。对于高效率求解模块而言，几何光学光线追踪方法(Geometrical Optics Ray Tracing Method)是目前解算效率相对于精确求解器而言效率较高的一种方法，隶属于一种几何理论散射(GDT, Geometrical Theory Diffraction)方法，适用于复杂广域电磁环境中对频率无关的电磁场环境进行分析。

依照Fermat原理和能量守恒定律，按照传统光线特性获得反射和散射。

(15)

在几种全波精确分析方法中，时域有限差分法(FDTD)具有的优势，使其近年来在电磁仿真领域中的应用获得的极大发展[9]。采用FDTD方法完成精确电磁场参数的解算，建立各电磁场和电磁流存在的本构关系：D=εE,B=μH,J=σE,Jm=σmH, 其中，E,H,D,B分别是电场强度、磁场强度、电位移矢量和磁感应强度;J，Jm分别是电流密度和磁流密度，它们分别是空间位置和时间的函数。ε，μ分别是媒质的介电常数和磁导率，σ，σm分别是电导率和导磁率。考虑直角坐标空间中的无源、非色散、各向同性、线性介质，可以将旋度方程式转化成六个标量方程。为了将标量方程中的各电磁场分量在空间和时间上离散，K.S. Yee将空间按立方体分割，并把电磁场的六个分量配置在网格的边沿和表面中心点上，如图5。

图5 基本Yee网格与其中的电磁场配置

为了便于分析，建议在空间上对Yee网格中每个节点进行编号，节点的编号和其空间坐标位置按照下面的方式对应起来：

(i,j,k)=(iΔx,JΔy,kΔz)

(16)

(17)

其中Δx，Δy，Δz分别表示在x，y，z方向上的Yee网格空间步长，i，j，k为整数，Δt为时间步长。

考虑到时间上电场和磁场有半个时间步的变化，按照Yee网格上的电磁场量配置，需要利用一阶导数的二阶精度中心差分近似式如下，其中Δu是步长间隔。

(18)

(19)

2.3 复杂多场耦合系统优化求解

最终的优化器所使用的方法主要有两类：基于梯度的共轭梯度类方法用于局部求解区域的快速极值搜索，以及进化类的全局寻优算法。这两种方法对于解空间的优化具有相互印证，相互支撑的作用。

基于梯度的共轭梯度类方法，每次迭代都会修正迭代方向，根据历次迭代的梯度方向及其正交方向，选择新一次迭代的收敛方向。对于给定的被优化函数：

(20)

(21)

(22)

(23)

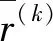
基于进化类的优化算法，所采用的方式与共轭梯度方法有很大不同。为了解决多目标优化问题，提升进化效率，减少进化种群数目和代数，本文采用目前较为流行的NSGA-II(改进的非支配排序遗传算法)，提升迭代寻优质量。

NSGA-II算法是在原有的NSGA算法基础上改进而来的算法，提升了算法效率，引入竞争策略扩大了采样空间，并使用拥挤度的概念，将个体均匀散布在Pareto推进前沿上，保证了种群的遗传特性多样性。NSGA-II算法有以下几个基本步骤：

(5)计算每个非支配层中的拥挤度；

(9)重复步骤迭代优化。

随着迭代操作的不断完成，对于每一代都会形成在目标空间中推进的Pareto前沿。在这些推进前沿中，需要通过一定的选取策略完成对最终优化设计参数的提取。一般使用加权方法在优化结束的最后一代的Pareto推进前沿面上选取最符合需求的最优解。

3 结 语

高精度、高性能电子装备设计的发展，经历了机电分离、综合与耦合三个阶段[10]，对机载电子系统来说，为了解决SEMF-MFCS的“机-电-磁-气动”复杂多场耦合问题，本文提出了一种求解思路，拟通过分析耦合理论关系及其影响理论，来进行系统耦合与优化研究。对于气动、结构、电性能、电磁性能之间的耦合分析，其单场分析方法十分成熟，但要研究建立起一套适用于机载电子SEMF-MFCS的分析方法，建立适用于任务目标而设定的多学科优化目标函数、多场之间耦合关系、耦合仿真与优化流程，是开展“机-电-磁-气动”复杂多场耦合系统技术研究的必须课题，这也是文献[2]反复强调的，需要加强基于模型的系统工程研究方法，推进MBSE工程，强化面向作战需求的联合设计与仿真，实现最优目标。

本文针对SEMF-MFCS提出的研究方法与思路，是基于前期工程经验、单学科仿真分析、跨学科优化探索等技术基础进行综合研究与分析提出的。虽然目前阶段针对具体案例开展建模仿真还比较有限，结果的支持还不够完善，但所提出的研究方法和解决思路，可为后续机载电子“机-电-磁-气动”多场耦合系统研究工作提供一定参考，对研究其“机-电-磁-气动”多场耦合问题具有一定借鉴意义。由于存在跨行业、跨专业联合设计与仿真的难度，亟待进一步推进基于该“机-电-磁-气动”耦合系统的深入研究，针对典型用例开展设计、仿真，构建原型系统，对本文提出的SEMF-MFCS耦合影响机理进一步摸底、测试与验证，对“机-电-磁-气动”多场耦合系统进行建模仿真、优化，并基于优化结果进一步进行工程验证，进而建立起一套完全紧耦合的SEMF-MFCS数学模型，更好地协同好SEMF-MFCS联合设计与仿真，以期系统设计的最优结果。