嵌入式模糊集数据库的FCM增量式聚类算法研究
斯亚民
(上海财经大学浙江学院,浙江 金华 321013)
0 引 言
嵌入式模糊集数据库技术被广泛应用在各种网络或大规模集成系统中,对各种系统重要数据存储具有重要意义[1]。嵌入式模糊集数据库中数据信息的管理与调度通常利用云计算与云储存实现[2],对嵌入式模糊集数据库中原始数据与新增数据进行准确分类与整合,极大提高了人们利用数据库进行日常工作的工作效率。
以往对嵌入式模糊集数据库中数据检索、分类、整合与挖掘通常采用小波变化算法、向量机分类挖掘算法等[3]。文献[4]方法提出基于AutoEncoder的增量式聚类算法,利用AutoEncoder学习数据样本的特征,进行低维特征整合,实现模糊数据库的增量聚类。该算法未设计滤波去噪功能,数据挖掘的过程中抗干扰性能差,导致聚类结果不准确。文献[5]方法提出基于多代表点的大规模数据模糊聚类算法。先对海量数据进行分块,对每个数据块逐一聚类,聚类时使用多个代表点描述捕捉数据的潜在结构和各个类信息,完成数据库增量聚类。该算法迭代次数过多,运算过于复杂,无法有效聚类动态数据,导致数据聚类效率较低。
为解决上述问题,提出对嵌入式模糊集数据库的FCM(模糊C均值(Fuzzy C-means算法))增量式聚类算法进行研究。先根据嵌入式模糊集数据库的结构,构建了数据信息流模型。采用自适应级跟踪滤波器对干扰进行抑制。关键步骤是引入了FCM增量式聚类算法,来动态地调整数据库中数据的聚类过程,得到高精度的数据聚类结果。且通过实验验证得出,该算法具有较高的聚类精度和聚类效率。
1 嵌入式模糊集数据库增量式聚类算法
1.1 嵌入式模糊集数据库数据信息流模型
将信息库数据调度目标信息与FCM聚类实施收敛性测试,初始化聚类中心,重组嵌入式模糊集数据库结构,将待推荐检索数据的时间变多径关联维代入数据库结构中去,对冗余干扰实施滤波处理,形成嵌入式模糊集数据库数据信息流模型。
1.1.1嵌入式模糊集数据库结构分析

(1)
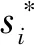
(2)
Fd(Ci)=Fn(Ci)+Fo(Ci)
(3)

1.1.2构建嵌入式模糊集数据库信息流模型
依据上小节分析的嵌入式模糊集数据库结构,构建嵌入式模糊集数据库待挖掘信息流模型。嵌入式模糊集数据控中待挖掘数据特征用WS表示,设WS概率分布均匀,融合聚类分析经线性调频解扩三阶自相关特征的信息流内指定数据,离散控制嵌入式模糊集数据中负荷信息流时间序列{x(t0+iΔt)},i=0,1,…,N-1,VMj表示过载数据信息流矢量长度,则基于待推荐检索数据的时间变多径关联维在嵌入式模糊集数据库结构中公式如下:
x(t)=λRe{an(t)e-j2πfcτn(t)sl(t-τn(t))e-j2πfct}
(4)
(5)

在嵌入式模糊集数据库信息流模型中,通过自适应级跟踪滤波器抑制数据库挖掘过程中受到的干扰[10],对冗余干扰实施滤波处理,自适应级跟踪滤波器输出函数见公式(6):
(6)
其中,A表示自适应级联滤波幅值,m与ρ表示待挖掘数据干扰滤波阶数与差值系数。Ta表示待挖掘信息数据码元宽度,设Ta=1/Ra,滤波处理后形成嵌入式模糊集数据库数据信息流模型为:
(7)
自适应级跟踪滤波器对数据挖掘过程中的干扰因子进行了抑制和滤除,因此经过滤波处理后,构建的嵌入式模糊集数据库信息流模型提高了抗干扰能力,数据挖掘过程所得到的数据结果更加准确。在此基础上,采用FCM增量式聚类算法获取分离度与凝聚度评价数据库中数据聚类结果,依据聚类结果决定该数据需要插入或删除,进而通过自适应FCM增量式聚类算法实现数据库的增量式聚类。
1.2 自适应FCM增量式聚类算法
增量式聚类算法是在新聚类计算过程中融入前期聚类运算结果。采用自适应FCM增量式聚类算法提高嵌入式模糊集数据库数据计算效率,嵌入式模糊集数据库中的更新数据对象集操作过程为插入数据与删除数据,使该聚类簇删除掉造成该聚类只剩下一个孤立点。在FCM聚类算法的基础上,基于凝聚度与分离度所得FCM增量式聚类算法。
1.2.1插入数据与删除数据
原始数据库中的数据集采用FCM聚类方法操作后,操作剩下数据与新增数据全部列入新增数据集中[11],新增数据集与通过聚类操作后数据集会形成情况如下:
(1)已有聚类不受新增数据影响,新增数据与原有聚类无任何联系。新增数据形成新的聚类或者不形成聚类作为孤立点存在,若该点在后续计算中被加入新的聚类中,则认为该点不是真正的孤立点;若孤立点直至计算终止仍然为孤立点,则计算终止后将它删除,
(2)新增数据被已有聚类接收,原有聚类增大,除此之外的聚类无变化。
(3)新增数据可同时被多个聚类接收,与多个聚类相似度高,因此可将相似的几个聚类通过该新增数据合并为新聚类,则与新增数据无关的聚类不发生变化。
(4)由于新增数据的插入,使原有聚类密度与分布受到影响而形成分裂[12],一个聚类可分裂成两个聚类或者多个聚类。
数据对象集内的数据删除也会形成以上分裂情况,从而将一个聚类由于某个数据的删除分裂成两个或者多个聚类。将数据直接删除对其它聚类不会产生影响[13],但有时因删除数据为此聚类中主要数据,因此将该数据删除后会使该聚类簇删除掉造成该聚类只剩下一个孤立点。
1.2.2增量式操作
用分离度与凝聚度来评价嵌入式模糊集数据库中数据聚类结果。假设聚类中一个簇,可通过将该簇分为多个子簇优化其凝聚性[14]。假如聚类中两个或多个簇分离性差但是凝聚性较高,可将其合并为一个簇。
为使聚类结果分离度与凝聚度均达到较高的值,在FCM聚类算法的基础上基于凝聚度与分离度所得的FCM增量式聚类算法如下:
采用欧式距离表示数据x与数据y间的距离,∀x,y∈RP,该算法距离公式如下:
(8)
聚类中代表相似与紧密性的凝聚度公式为:
(9)
聚类中代表互相差异性的分离度公式为:
separation(Fi,Fj)=d(fi,fj)
(10)
其中,fi表示Fi聚类的中心,fj表示Fj聚类的中心。

通过式(8)得到新增数据点xnew与聚类间距Di=d(xnew,fi)利。
当计算结果Di>maxdist时,则该点不属于之前的聚类,该点作为新聚类的中心,后续计算中与该点具有相似性加入到该聚类中。
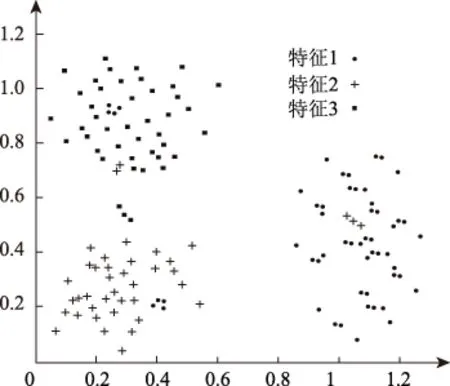
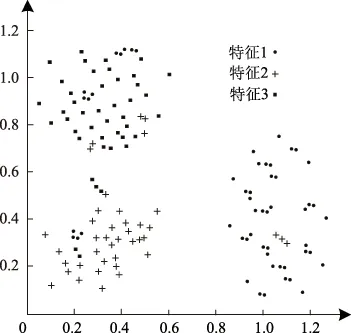
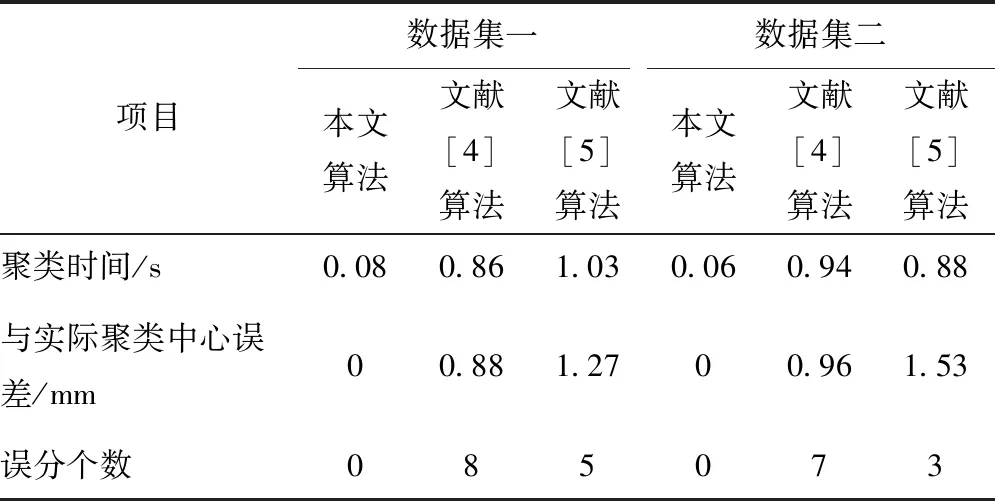
当计算结果Di 当计算结果Di 将所有新增数据按如上步骤重复直至结束。 为获取准确的聚类算法结果,在新增数据聚类后,对新增数据插入的簇利用公式(9)运算凝聚度,对比插入新数据后的聚类cohesion(Fi)′与未插入新数据前的聚类cohesion(Fi)相似与紧密性是否有改变。利用数值α作为凝聚度是否满足要求的衡量数值[15],α值通常由大量实验获取。当|cohesion(Fi)′-cohesion(Fi)|<α时,说明插入新数据后的聚类凝聚度值符合要求,无需进一步处理;当|cohesion(Fi)′-cohesion(Fi)|>α时,说明插入新数据后的聚类凝聚度值不符合要求,利用自适应FCM聚类算法对该类进行进一步分裂。 算法1具体过程为: 算法1 初始聚类中心算法 Entering 待分类的类S Export 分裂时的初始聚类中心F和聚类个数jj Initialization (S) Start (1)W={x1,x2,…,xm}; /*待分裂聚类内数据包含m个数据,W为候选聚类中心为该聚类中每一点时的数据集*/ (2)F=φ; /*F是初始聚类中心集*/ (3)For(i=1;i<=m;i++) Len[i]=Calculate Number(xi,t); /*计算球体范围圆心xi与半径t内包含数据个数*/ (4)For(j!=1,j=1;j<=m;j++) If ‖xj-xi‖<=r then Tag xj; /*标记xj邻域范围包含的点*/ Endif (5) simultaneously(W≠) { j=1; Species(len[i]); Fj←len[1]相应数据xi;/聚类中心选取密度最大点/ F←Fj; /*初始聚类中心融入聚类中心集F中*/ Delete 含有xi的xj; W←W-{xj};/*更新聚类中心集*/ j=j+1} (6)back(F,j) End 1.2.3增量式聚类 依据上述聚类结果,采用自适应FCM增量式聚类算法(AIFCM),实现嵌入式模糊集数据库中数据的增量式聚类。算法2具体过程如下: 算法2 自适应FCM增量式聚类算法 Entering 对已有数据对象的聚类结果F={F1,F2,…,FC},新增数据Xnew,阈值α Export Fi为最终聚类结果 AIFCM(F,xnew,α) Start (1)如果是插入的数据,那么 (2)(i=1;i<=c;i++) (j=1;j<=c;j++) (Fi,Fj)的可分性用式(11)计算。 (3)当最大距离=最小距离Maximum distance(Fi,Fj)时: (4)(i=1;i<=c;i++) Di=d(xnew,fi) (5) If Di>Maximum distance then c=c+1; Otherwise If count(i)==1 then Xnew→Ci; /Xnew加进Ci聚类内/ If |cohesionFi)′-cohesion(Fi|>α then break up(Fi);/分裂聚类Fi/ c=c+j End if Else Ci→Ci+Cj; /*融合Ci与Cj*/ c=c-1; Xnew→Ci; /*Xnew加进合并后的聚类Ci中*/ End if End if /*插入操作*/ Otherwise /*删除操作*/ Delete xnew from Ci ; If |cohesionFi)′-cohesion(Fi| >α then break up(Ci);/*分裂聚类Ci*/ c=c+j End if Else (6)back (Ci); End 通过以上过程,实现嵌入式模糊集数据库的增量式聚类。 通过两组实验数据集验证本文算法对嵌入式模糊集数据库数据聚类效果,将本文算法与文献[4]提出的基于AutoEncoder的增量式聚类算法、文献[5]提出的基于多代表点的大规模数据模糊聚类算法两种增量式聚类算法进行比较。 采用系统为Windows 7.0,Intel ivy Bridge处理器,内存接口为DDR3-1600,运行内存为4GB,主板为i965的计算机配置作为仿真实验平台。实验基于Simulink和MATLAB软件,利用Java进行编程,实验数据集采用该平台生成的210个范围为[0 1;0 1]的嵌入式模糊集数据样本集,数据集共有两个,两个数据集进行等量化分,分别记作数据集一和数据集二,由此避免实验结果的偶然性。该数据库含有三类数据样本,每类样本数量为70个,利用180个样本进行初始聚类数据,剩余30个样本作为增量聚类数据。 三种算法实验数据集一的聚类结果见图1、图2、图3。 图1 本文算法对实验数据集一的聚类结果 图2 文献[4]算法对实验数据集一的聚类结果 图3 文献[5]算法对实验数据集一的聚类结果 根据图1~图3可以看出,采用文献[4]算法对数据集一进行聚类,在三组聚类结果中,都混有少量的其他组特征,但混入量较小;采用文献[5]算法对数据集一进行聚类,在三组聚类结果中,都混有大量的其他组特征,聚类效果并不明显;采用本文算法对数据集一进行聚类,在三组聚类结果中,完全没有混入的其他特征量,聚类结果十分准确。 实验数据集二采用国际上通用于数据聚类的IRIS嵌入式模糊集数据库中数据集,该数据库包含于UCI数据库,是一类多重变量分析的数据集。该数据集中包含四维样本点共150个,该数据库含有三类数据样本。将该数据库随机分成两组,一组内含有120个样本为聚类初始样本,剩余30个样本作为增量聚类样本。利用三种增量聚类算法对实验数据集二进行数据聚类,聚类结果如图4、图5和图6所示。 图4 本文算法对实验数据集二的聚类结果 图5 文献[4]算法对实验数据集二的聚类结果 图6 文献[5]算法对实验数据集二的聚类结果 根据图4~图6可以看出,数据集二中的三种特征与数据集一不同,但聚类条件和聚类方式均相同,那么,采用文献[4]算法对数据集二进行聚类,在三组聚类结果中,都混入了大量的其他特征,且数据并不集中,分布散乱;采用文献[5]算法对数据集二进行聚类,在三组聚类结果中,虽然明显地实现了聚类,但少量混入了的其他组特征;采用本文算法对数据集二进行聚类,在三组聚类结果中,完全没有混入的其他特征量,聚类结果十分准确。对比上述两次实验结果得出,本文算法聚类效果优于其他两种方法,可将特征精准的分类,没有错分样本。另两种算法虽然可以将大部分特征分类,但是分类并不精准。主要原因在于本文算法通过自适应级跟踪滤波器抑制数据库挖掘过程中受到的干扰,对冗余干扰实施滤波处理,构建的嵌入式模糊集数据库信息流模型提高了抗干扰能力,数据挖掘过程所得到的数据结果更加准确,避免其他组特征混入,使聚类数据集中。 统计三种算法对实验数据集一和二进行聚类的聚类性能,结果用表1描述。 表1 不同算法的聚类性能比较 分析表1可以看出,本文算法对嵌入式模糊集数据库中数据进行聚类运算时用时最少,并且所得聚类中心与实际聚类中心差距极小,在两个实验中没有错分样本,说明了本文算法的有效与准确性。主要原因在于本文算法采用自适应FCM增量式聚类算法,提高嵌入式模糊集数据库数据计算效率,进而缩短了聚类时间。降低了聚类中心误差。 实验为了验证本文算法的大数据聚类性能,采用大数据样本验证本文算法对嵌入式模糊集大数据库增量聚类的有效性。在Matlab平台生成20000个嵌入式模糊集数据样本,将其中10000个数据样本为初始聚类数据,其余10000个样本分为10次增量加入初始数据库中,检测三种算法的增量聚类准确度,有效性。三种算法进行10次增量数据后聚类精准度和时间见表2和表3。 综合分析上述两表可得,本文算法聚类大规模数据增量时依然可以保持很高的聚类准确度,并且聚类用时很短,说明本文算法对嵌入式模糊集数据库进行增量聚类,具有较高的精度和效率。主要原因在于本文算法在FCM聚类算法的基础上,进行凝聚度与分离度FCM增量式聚类,使聚类结果分离度与凝聚度均达到较高的值。 表2 三种算法10次增量准确度 表3 三种算法对大数据的平均聚类时间 目前对于嵌入式模糊集数据增量式聚类算法研究较少,数据库中数据挖掘结果应随着数据库中数据的更新而进行更新,本文提出新的嵌入式模糊集数据库增量式聚类算法,在嵌入式模糊集数据库数据信息流模型中加入了自适应级跟踪滤波器,抑制数据库挖掘过程中受到的干扰,将冗余干扰实施滤波处理,经处理后的算法对噪声样本敏感,可将噪声点区分出来,使处理后的数据受外界干扰较小;在此基础上采用自适应FCM增量式聚类算法,实现数据库中数据的增量式聚类,该算法不随增量数据的改变而改变聚类数量,增量式聚类效果较好。经过大量实验验证本文算法完成了嵌入式模糊集数据库中数据的高速、精准聚类,对大规模增量数据聚类效果明显,准确率高,应用价值高。
2 实验分析

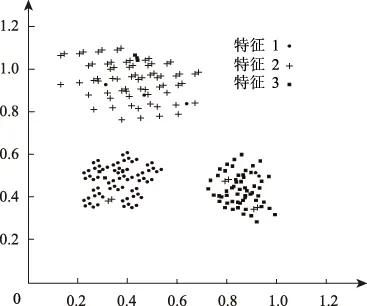
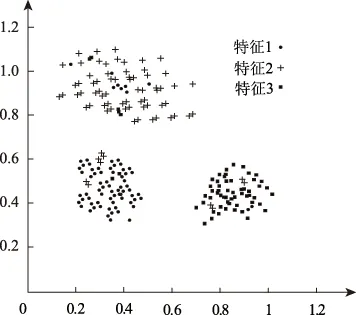


3 结 语

