公共自行车调度路径优化算法
马智超, 徐海涛
(杭州电子科技大学 计算机学院,浙江 杭州 310018)
0 引 言
研究公共自行车调度路径优化问题对提高市民对公共自行车使用的满意度,缓解交通拥堵,绿色出行具有重大意义。目前已经有一些人对该问题进行了研究,但相应的模型和算法还需要改进。文献[1,2]模型的优化目标只考虑了油费,文献[3]的模型考虑了用户的满意度,分别提出软时间窗和硬时间窗模型。为了求解自行车调度问题,文献[4]提出了改进的遗传算法,文献[5]提出了自适应遗传算法,文献[6]提出了用改进的蚁群算法,文献[7]提出了模拟退火算法。这类算法均容易陷入停滞。智能水滴算法在短时间内可以得到更优的解,并在多个领域得到验证,文献[8]用其求解旅行商问题(TSP),文献[9,10]用其求解车辆路径问题,但该算法本身也具有陷入停滞特点。变邻域搜索具有很强的搜索能力,从文献[11,12]可以看出,如果变邻域搜索有一个合适的领域结构和较优的初始解,其效率将会大大提高。为此本文将二者融合。
本文提出了一种带有混合时间窗的数学模型,既考虑了用户的满意度又考虑了调度成本。提出了一种混合智能水滴算法,与变邻域搜索融合,提出了两种适用于路径优化问题的邻域结构,提出了节约算子、启发式因子和最大最小调制的改进策略。仿真对比实验验证了算法的有效性。
1 问题描述与构建数学模型
1.1 问题描述
假设有不同的工作区域,每个工作区域都有一个调度中心用于管理属于同一区域的自行车站点。系统会一直检查站点的状态,看是否需要调度。系统会计算出相应的需求,包含这个站点需要调度的自行车数量,最佳调度服务时间以及运输车和各个站点的位置信息。如何根据这些信息来计算调度方案,是本文要研究的问题。调度方案包括需要派出几辆运输车、每辆运输车的行驶路线。
1.2 构建数学模型
假设有1个调度中心({0}),公共自行车租赁站点N={s1,s2,…,sN},需要K个运输车,每个最多可载Q辆自行车;运输车到达站点si的时刻为ti;从站点si到sj所需要的时间为tij(s),路程为dij(km)。wij是运输车从si到sj运行过程中装载的自行车数量,wi是在站点si的等待时间。定义Cw为每秒给工作人员的薪资,Cp为单位里程的油费,单位均为人民币。di为站点si的调度量,如果di≥0,就意味着si需要辆di辆自行车,否则就意味着该站点需要带走di辆自行车。该调度的服务时刻必须在时间窗[ci,di]内,且最佳服务时间窗为[ai,bi]。本文定义惩罚条件:如果运输车对站点vj服务的时刻在[ai,bi]外且在[ci,di]内,系统将予以惩罚,如式(1)所示
(1)
如果运输车k从站点vi向站点vj运行xijk=1,否则,xijk=0。如果对站点vi服务的是运输车k,yik=1,否则,yik=0。则优化目标如式(2)所示,表示车辆运行的成本,既包括运输车所耗油费,又包括不满足时间窗的惩罚成本
(2)
式(2)需要满足以下几个约束条件
0≤dj+wijk≤Q(i,j∈N∪{0},k∈{1,2,…,K})
(3)
|di|≤Q(i∈N∪{0})
(4)
(5)
(6)
cj≤ti+si+tij-k(1-xijk)≤dj(i,j∈N∪{0})
(7)
式(3)指运输车在调度过程中,其车上的自行车的数满足车辆的载运能力;式(4)指每个租赁点的调度量不超过运输车的最大载运能力;式(5)指运输车辆均从车场出发最终回到车场;式(6)指每一个租赁点仅由一辆运输车辆服务;式(7)指运输车在某租赁点的服务时刻必须满足时间窗约束。
2 改进的混合智能水滴算法
2.1 算法步骤
水流在地面上流动会自动绕开障碍物,水流可以看成水滴iwd组成的群体,水滴流动时速度为veliwd,水所携带泥土量为soiliwd,路径泥土量矩阵为sw,各量会随着水滴在河道中的流动而发生变化直至找到最优路径。定义arc(i,j)代表从站点si到sj的路径,TIB为每次迭代的最优解。为了使其可以求解调度路径优化问题,且能够提高算法的效率,对水滴算法进行了改进,改进后算法一般步骤为:
1)初始化算法的各个参数,如更新参数av,bv,cv,as,bs,cs等。
2)重复步骤(3)~步骤(7)步操作直到迭代次数达到iterMax。
3)每只雨滴重复步骤(a)~步骤(c)操作直到所有雨滴都构造了解决方案:
a.当一个雨滴完成了对所有站点的调度,则计算下一个雨滴,否则,转步骤(b);
b.选择下一个要服务的站点;
c.更新水滴当前动态变量。
4)从本次迭代中得到的所有水滴完整路径中,找到其中最优解。
5)更新最优路径上的泥土量。
6)如果迭代次数大于一定的值后执行变邻域搜索。
7)更新全局最优解TTB:如果cost(TIB) uij=di0+d0j-dij,(0∈{depot};i,j∈{1,2,…,N}) (8) 则改进的概率矩阵为 (9) (10) 式中r=0.01,FV为可以访问的站点集合。 雨滴从调度中心出发,根据赌轮法按照式(9)来选择FV中的站点来服务,判断如果对站点进行调度服务,是否能满足约束条件,包括时间窗和容量约束,如果FV中站点都不满足约束条件则返回调度中心,将水滴的动态变量恢复初始值,执行换车操作。如果满足约束条件了,则该站点即为雨滴要服务的下一站点。 在得到要服务的站点sj后,将该站点添加到路径中,更新当前的路径,根据tj=ti+tij,Q(j)=Q(j)+dj更新到达新站点的时间tj和运输车装载量Q(j)。然后判断是否满足惩罚条件,如果满足惩罚条件,根据式(1)增加惩罚值。 更新水滴中携带的泥土量soiliwd和路径arc(i,j)中的泥土量sw(i,j) soiliwd=soiliwd+Δsoil(i,j) (11) sw(i,j)=sw(i,j)-αΔsoil(i,j) (12) (13) (14) 式中TTB为当前最优解,n为水滴到达目的地的个数。 设在第t迭代的最优解为TIB,更新泥土量 (15) 变邻域搜索主要包含两个步骤邻域变换和局部搜索: 1)用智能水滴算法的最优解作为初始解s,sb=s。 2)重复步骤(3)步操作直到终止条件满足,最后sb即更新后的解。 3)在邻域内变换解的结构s′:=Nk(s),在每种邻域结构里执行邻域搜索:s″:=localsearch(s′)。若新解s″的代价值小于sb,sb:=s′,依此继续在邻域结构搜索。其中,Nk(s)为s的k邻域结构。 本文提出了两种邻域结构,如图1所示,在图1中最上部分为从最优解中随机选取的两个路线,后两个图给出了子路线交换和站点重置法,据此可以得到两种邻域结构N1(s),N2(s)。 图1 两种邻域结构说明 本文共设计了10个样例来测试算法,表1是样例1数据,其他样例数据格式如表1所示。其他参数如下:as=1,bs=0.1,cs=1,av=1,bv=0.1,cv=1,Cp=0.6,Cw=0.3,α=1,β=1,tij=150dij,ci=ai-120(s),di=bi+120(s)。 表1 实验数据样例 本文提出的算法对表1数据进行求解,求得结果模拟如图2所示。 图2 样例1运算结果模拟 计算得出共需要4辆车,每辆车的路线如下所示: 第一辆车:1→18→3→21→8→6→10→12→1 第二辆车:1→16→17→24→19→4→1 第三辆车:1→2→13→22→5→1 第四辆车:1→7→23→14→1 算法对10个样例测试对比结果,如表2所示。其中,IHIWD是本文最终的算法,IWD—1是本文提出增加了启发式因子和节约算子以及最大最小调制机制后的改进智能水滴算法。IWD是改进的智能水滴算法,对这个算法改进是为了使其可以用于求解本文中的模型,可以用来对比。如图3。 表2 样例的测试结果 图3 每代路径最小代价对比 从表2中和图3可以看出改进算法的效果,图3为样例4 测试结果,显示两种算法每次迭代中路径的最小代价的对比,可以看到IWD—1优于IWD。如果不对水滴中的泥土量限制,就会出现某条路线泥土量过多过少,算法会过早陷入停滞。节约算子和启发式因子是一种贪心策略,偶尔的贪心策略可得到更优的解。而对其融合变邻域可以提高搜索全局最优解的能力。 1)本文对公共自行车调度路径优化问题建立了数学模型,独特地从到达站点时间的角度去建立混合时间窗,以满足实际应用。对模型的建立既考虑了调度成本又考虑了居民对自行车使用的满意度。 2)本文提出了一种求解该问题的改进的混合智能水滴算法,在算法改进上,融合了改进的变邻域算法,并引入节约算子等策略,使得得到的结果更优。通过算法对比验证了新算法的有效性和优越性,并分析了原因。 本文的算法还存在一些不足,解决方案中没有计算出初始时每辆车的载运量和最佳出发时间,这个是未来工作中需要考虑的,下一步工作会对公共自行车智能调度问题和算法融合策略进行更深一步研究。2.2 调度服务站点的选择

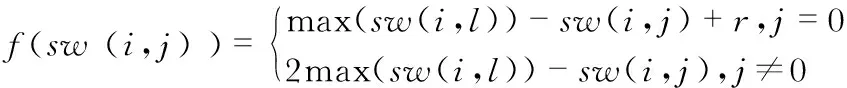
2.3 水滴动态变量的更新

2.4 路径泥土量的更新
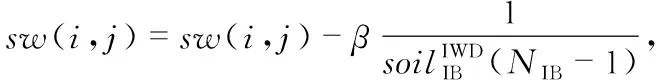

2.5 改进的变邻域搜索

3 仿真实验与算法分析
3.1 实验设计

3.2 实验算法对比分析
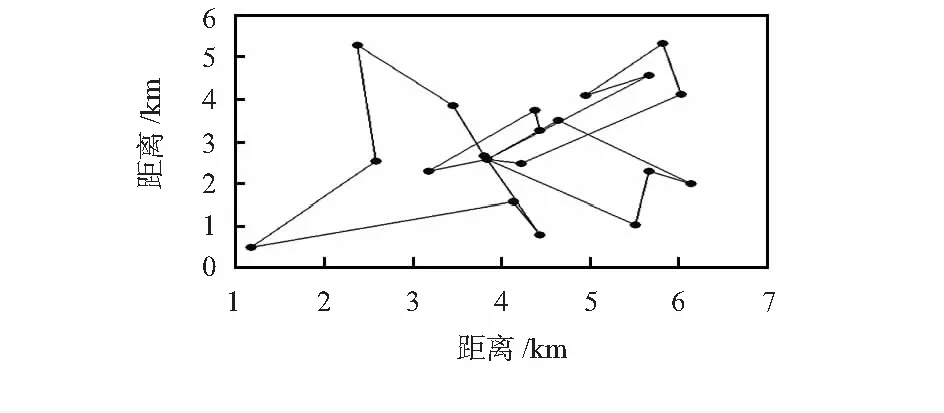
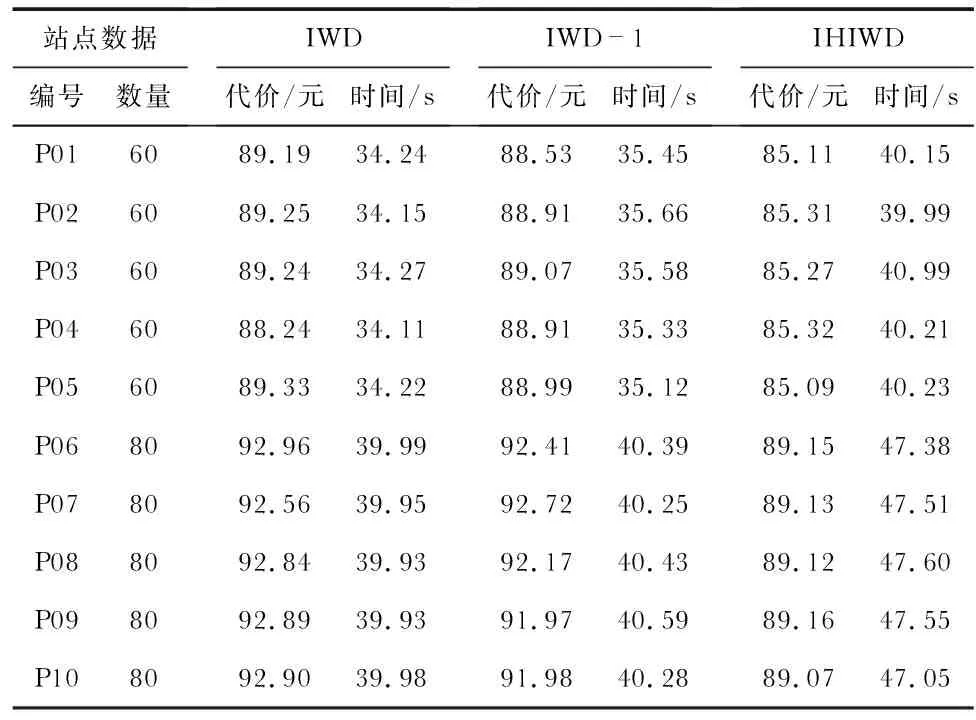

4 结束语

