基于SMC和AFEKF的PMSM无传感控制*

朱 军， 吴宇航， 孟祥宾， 李紫豪

(河南理工大学 电气工程与自动化学院，河南 焦作 454000)

0 引 言

电机无位置/速度传感器控制是永磁同步电机(permanent magnet synchronous motor,PMSM)在高性能驱动系统中的一个重要发展方向[1]。随着20世纪70年代以来，无传感技术[2]飞速发展，常用的电机无传感几种方法中[3～9]，卡尔曼滤波(Kalman filtering,KF)是一种线性无偏的最小方差估计算法[10]，在电机的无传感控制中，大多采用传统的扩展卡尔曼滤波(extended Kalman filtering,EKF)算法，针对EKF可能会出现的滤波发散的情况，文献[11]提出了在EKF的基础上加入渐消因子，使当前信息所占的比重增大，减小了陈旧信息的影响，使算法更加精确；Sage-Husa自适应滤波[12]原理简单、实时性好，在惯性导航中应用广泛。

目前，转速调节器均采用比例积分(proportional integral,PI)调节器或改进的PI调节器，针对基于EKF的无传感器系统的转速控制策略研究还较少。速度控制器除了要求响应快、精度高和调速范围广外，还要求对负载扰动和系统参数变化具有较强的鲁棒性。滑模速度控制器(sliding-mode speed controller,SMC)作为一类特殊的非线性控制策略[13]，在外界扰动或参数变化时会发生抖振现象，文献[14]提出了一种基于新型指数趋近律的滑模控制，有效地抑制了滑模控制器固有抖振问题，增大了趋近速度。

因此，本文根据传统EKF滤波易发散和实时性差的问题，提出了一种基于Sage-Husa自适应滤波器，并加入渐消因子的自适应扩展卡尔曼滤波(adaptive fading EKF,AFEKF)方法来预测转子的位置和速度。并针对传统PI速度控制器的速度超调及滑模控制会出现的抖振情况，设计了一种改进的基于指数趋近律的滑模控制器。

1 系统模型

1.1 数学模型

本文PMSM用于EKF数学模型选择在α—β静止坐标轴系以避免d—q坐标系在建模时产生非线性和增加计算时间，电流状态方程为

(1)

式中iα,iβ分别为α—β坐标下的定子电流；Rs,Ls,ψf,ω,θ分别为电机的定子电阻值，定子电感，转子永磁磁链，转子电角速度和转子位置角。

1.2 状态方程

状态方程描述状态向量的行为。本文定义状态向量为x=[iαiβωθ]T，则本系统对应的非线性方程表述为x(t)=f[x(t)]+Bu(t)+w(t),进行线性化并离散

Xl=Φk,k-1Xk-1+BUk-1+Wk-1

(2)

1.3 观测方程

观测方程是用来描述状态向量和观测值之间的关系。因为α—β轴系的定子电流值是较易测量的电机参数，所以将y=[iαiβ]T作为输出变量，系统对应的非线性方程为y(t)=h[x(t)]+v(t)。其线性离散方程为

(3)

2 SMC控制器

2.1 新型趋近律

对于指数趋近律，可通过增大k值的同时减小ε值加速趋近过程同时减小抖振，但因为存在较大的k值与等速项εsgn(s)，使系统并不能在理论上消除抖振。为了克服指数趋近律的缺点，本文设计了一种新型变指数趋近律

(4)

式中 -ε|x|sgn(s)为变速项，-ks为指数项。当系统的状态变量距离平衡点较远时，系统主要以变速和指数两种方式快速趋近滑模面。当系统的状态变量与滑模面的距离较近时，指数项趋近于零，这时变速项起主要作用。当系统的状态量在稳定的状态下趋近于零时，由于滑模控制率的作用使状态变量x进入滑模面并向原点运动，此时的变速项-ε|x|sgn(s)将不断减小，最终稳定在原点，使得造成抖振现象的变速项系数为零，从而抑制抖振现象。

2.2 滑模速度控制器设计

为了便于滑模速度控制器的设置，在d—q坐标系下建立永磁同步电机的数学模型

(5)

对于表贴式PMSM，采用id=0的转子磁场定向控制可获得较好的控制效果，可获得如下数学模型

(6)

(7)

(8)

2.3 系统稳定性分析

为了分析滑模控制器的稳定性，定义Lyapunov函数为

(9)

由于ε>0,k>0，保证了SMC稳定性的条件<0，从而能保证系统能稳定进入滑膜状态。

3 AFEKF算法

EKF算法的缺点为实时精度不够和容易发散。为此，本文提出了一种基于Sage-Husa的AFEKF算法。

针对EKF用于估算PMSM的速度和位置可能会存在滤波发散的情况，本文根据文献[11]采用加权衰减记忆滤波法，采用新的滤波算法加重了当前信息的比重，增大了对陈旧信息的遗忘，充分利用了新数据所包含的信息，以此来抑制滤波的发散。本文在EKF的基础上，引入一个渐消因子s2，使EKF算法中一步预测均方差和滤波增益公式变为

(10)

针对EKF通过试凑得到系统噪声Q和观测噪声R，在滤波估计过程中认为其固定不变，故在实际中存在实时性差和性能不佳的问题，本文引入基于Sage-Husa的自适应滤波器，在估计滤波的同时，利用观测数据的信息来进行递推，对滤波器噪声统计特性不断地进行在线实时估计和修正，进而提高滤波精度，得到估计状态的最优值。但直接使用该方法，容易使噪声统计二阶矩阵的估计k,k失去半正定性和正定性，导致滤波发散。有文献[16]指出R和Q不能同时被估计，只能在Q(R)已知时估计出R(Q)，否则由迭代递推出来的估计值与实际值会存在一个常值误差。而又由于输出方程式是线性的，不需要进行线性化计算，可将观测噪声当作零均值的高斯白噪声。因此，可得出简化的Sage-Husa滤波器

(11)

(12)

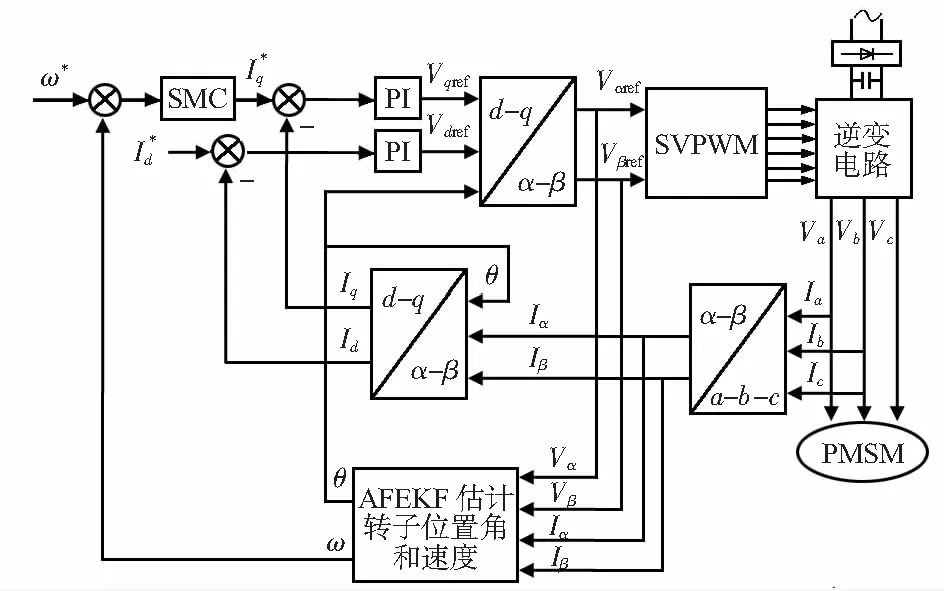
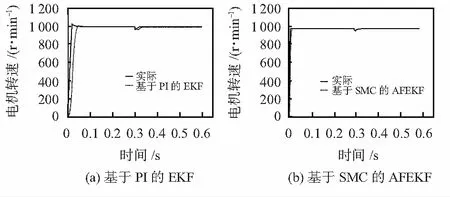
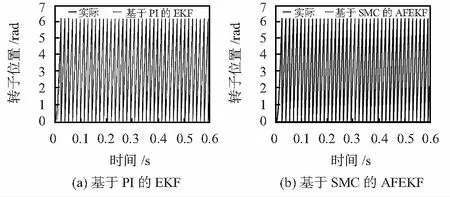
式中 E[ωk]=qk,E[(ωk-qk)(ωj-qj)T]=Qkδkj,dk=(1-b)/(1-bk+1),0

本文采用的基于Sage-Husa的AFEKF算法，主要是通过估计噪声方差与加入渐消因子相结合的方法，推算出最佳稳态增益矩阵Kk，使得增益矩阵Kk不断地与实际观测值相适应，并且在保证实时性的同时，最大程度地提高收敛速度，从而得出最优估计值k。具体的实现过程如图1所示。

图1 简化Sage-Husa的AFEKF算法的实现流程

无论是EKF还是AFEKF在对初始状态参数选择时，卡尔曼滤波增益K的计算与Q，R，P有关。而Q和R取值选择会极大影响系统估计精度及算法收敛性。通常情况下Q和R都是未知的，只能根据系统噪声和测量噪声不断试凑确定其的取值。初始设定与实际值可能有误差，但随着滤波步数的增加，新观测值的权重增大，其滤波输出值会逐渐接近系统的真实状态，而初始值误差的影响也会随着系统程序的运行逐渐消失；P0应选择一个较大的数；在整个估计中，AFEKF要保持观测噪声方差Rk=R0，这要求对观测值先验信息了解的边角充分且准确。本文根据前人的经验，经反复实验最终确定初始状态参数：x0=[0 0 0 0],P0=diag[0.5 0.5 200 5],q0=diag[0 0 0 0],R=diag[0.5 0.5],Q=diag[0.25 0.25 10 0.01]。

4 实验与结果分析

4.1 模型框图

图2为基于SMC和AFEKF的PMSM无传感器控制系统框图。本系统采用id=0控制策略，其控制结构是外环为转子速度环，内环为电流环的双闭环。其中内环控制器的输出信号Ud和Uq经过Park逆变换得到Uα和Uβ，电机相电流Ia,Ib和Ic经过Clack变换得到的Iα,Iβ。将Uα,Uβ,Iα和Iβ作为AFEKF模块的输入信号，并估算出转子位置角θ和速度ω，作为矢量控制的反馈控制。

图2 基于AEKF的PMSM无传感器控制系统框图

4.2 结果分析

MATLAB中建立如图2的仿真平台，电机用MATLAB中自带的PMSM模型，电机参数分别为：Rs=2.875 Ω ，Ls=0.008 5 H，pn=4，ψf=0.175 Wb，J=0.000 8kg·m2，转子初始位置为0。本文分别对基于PI速度控制器的EKF和基于SMC速度控制器的AFEKF两种算法进行仿真实验：预定转速为1 000 r/min，在0.3 s时由空载突加负载5 N，仿真持续0.6 s。图3为基于PI和EKF算法与基于SMC和AFEKF算法的系统转速波形；图4为2种算法的转子位置仿真波形。

图3 2种算法的转速曲线

图4 2种算法的转子位置

由图3可以看出，当电机由静止启动达到预定转速时，采用PI转速控制器的EKF无传感系统在初始阶段转速有超调、上升时间长，追踪效果较差，采用SMC转速控制器的AFEKF无传感系统在初始阶段转速无超调，响应快，追踪效果好；在达到预定转速保持稳定状态的0.3 s中，2种算法与实际转速均相差不大，误差范围在0.1 %以内；在0.3 s时突加负载5 N，图5为加载后0.3～0.6 s,2种方法与实际值的误差曲线，可以看出,采用SMC速度控制器的AFEKF相比PI速度控制器的EKF在突加负载时转速跌落较小，能更快更精确地追踪实际转速，速度估计按正弦规律收敛于实际转速，而基于PI速度控制的EKF在加载后更久达到稳定转速，且转速有所跌落，本文所提出的新算法最大速度偏差比传统算法减小了1.77 %，且稳定状态下转速误差下降了0.371 %。由图4可以看出，在启动和加载时基于SMC的AFEKF相比基于PI的EKF在位置估计精度更高，对图4局部放大，可以明显看出在同一时间内，新算法的位置估计准确度更高，最大位置误差比传统算法减小了0.45 %，更接近实际值。

图5 2种算法与实际转速的误差对比

5 结 论

本文为了使PMSM无传感控制更精确地估计速度、位置，提出了AFEKF算法，仿真结果表明，SMC和AFEKF性能均优于PI和EKF，且本文算法可以达到对历史统计数据的遗忘，又能应对PMSM运行过程中参数变化、环境噪声的影响，对电机速度、位置估计更精确。