水翼非定常空化流动中湍流模型研究
李雨濛,陈 晖,项 乐,张亚太
(西安航天动力研究所 液体火箭发动机重点实验室,陕西 西安 710100)
0 引言
近年来航天不断发展,液体火箭发动机作为重要的动力来源也不断更新换代。新一代液体火箭发动机以液氢液氧或液氧煤油作为推进剂,比冲高,推力大,工作时间长,在大型运载火箭上得到广泛应用。涡轮泵作为液体火箭发动机的核心部件,在高转速的环境下工作易导致涡轮泵内出现空化,影响液体火箭发动机的可靠性[1-5]。
空化作为水力机械中经常出现的一种现象,会造成水力机械性能明显降低[6],材料表面破坏,引起振动和噪声等[7-8]。空化对动态响应特性的改变会使流动内部出现不稳定性,多个国家在研究液体火箭发动机涡轮泵时都碰到过空化不稳定带来的问题乃至事故。例如,在日本H-2火箭的第8次发射中,空化不稳定诱发的脉动频率与泵前导流叶片固有频率相近,引起共振导致叶片疲劳断裂,转子失衡及摩擦,并最终导致发动机停机发射失败。为了减小空化不稳定带来的危害,各国学者做了多方面研究[9]。由于水力机械几何过于复杂,便从较为简单的水翼非定常空化入手。时素果等[10]研究了热力学效应对空化水动力脉动特性的影响,得到了水翼升力在非定常空化阶段的特征频率。Wang等[11]研究了附着空化流动,对空化初生进行了探究。Leroux等[12]对水翼的云状空化进行研究,发现翼型表面不同位置压强随时间变化不同,得到云状空化两种不同的动态特性。尹必行等[13]采用试验研究与数值模拟相结合的方法研究绕水翼ys930的非定常空化流场结构,得到片状空化和云状空泡两个不同的阶段。
实验研究依靠实验设备、实验人员和实验场地等条件,使得实验研究内容的多样性受到了限制。除了实验,数值仿真也是研究空化的重要手段。目前有3种方法可以计算湍流,虽然DNS和LES能提供更好的计算精度,但是会消耗大量计算资源,目前还无法广泛实现工程应用,现在工程上最常用的还是RANS方法。Launder和Spalding[14]提出了标准k-ε双方程模型,在RANS方法中预测结果更具有稳定性和可靠性[15],适用于绝大多数的工程湍流模型。空化流动是一种复杂的流动现象,包含湍流、相变、多相流、可压缩和非定常性等等。标准k-ε模型在处理时间相关流动上的缺陷使得对非定常空化的模拟存在一定误差[16]。有学者从标准k-ε模型的涡黏项入手,提出了一些修正方案。Johansen等[17]在标准k-ε模型的基础上增加滤波器提出FBM模型,并计算了方柱绕流的非定常流动,结果表明FBM模型部分提高了对非定常流动的预测能力。Huang等[18]将FBM模型和DCM模型[19]中的滤波系数加权,得到一种新的滤波模型FBDCM模型并用该模型计算了Clark-Y型水翼的绕流空化,结果显示FBDCM模型基于网格分辨率和当地流动的密度修正可以促进空化流动的非定常脱落。洪锋等[20]通过FBM模型和DCM模型中滤波项的比较选择新的滤波函数,发展出MFBM模型,同样仿真Clark-Y型水翼的绕流空化取得了较好的结果。以上3种修正的湍流模型与标准k-ε模型相比,都从不同程度上增强了预测非定常流动的能力,但这3种修正湍流模型之间目前还没有一个对比评价。
综上,本文分别选用原湍流模型和上述3种修正湍流模型,对Clark-Y型水翼表面的非定常空化流动进行模拟,通过与实验结果的对比,对不同模型修正方式的计算效果做出评价。
1 数值计算方法
1.1 控制方程
本文的数值方法采用均相流模型,混合流体被认为是各向同性的,相间无速度滑移,气相和液相有相同的速度和压力,则混合流体的密度表达式为
ρ=αvρv+(1-αv)ρl
(1)
式中:ρ为混合相密度;ρv,ρl分别为气相和液相密度;αv为气相体积分数。
在笛卡尔坐标系下,连续方程和动量方程分别为
(2)
(3)
混合流体中的气相输运方程为
(4)
式中m+和m-分别为气相中的蒸发源项和凝结源项,控制气体的产生与溃灭。
1.2 空化模型
Zwart等[21]结合简化的Rayleigh-Plesset方程,推导出的蒸发源项和凝结源项如下
(5)
(6)
式中:Ce和Cc分别为蒸发和凝结常数;RB为空泡半径;αnuc为不凝结气相分数。
该模型重点考虑了空化初生和发展时空泡体积变化的影响,适于模拟空化的非定常特性。
1.3 湍流模型
1.3.1 标准k-ε模型
标准k-ε模型由Launder和Spalding[14]提出,是在代数涡黏模型基础上发展得到的涡黏模型,与代数模型的主要区别是将涡黏系数与湍动能k及湍动能耗散ε联系在一起,包含部分湍流统计量之间的历史效应,有一定的物理依据,其控制方程为
(7)
(8)
湍流黏性系数μt表示为k和ε的函数,即
(9)
式中Pt为湍动能生成项。模型常数分别为:Cε1=1.44,Cε2=1.92,σε=1.3,σk=1.0,Cμ=0.09。
1.3.2 FBM模型
RANS方法的计算精度除了与网格尺寸有关外,还与流场的涡黏系数即雷诺应力有关。Johansen等人[13]认为标准k-ε模型对湍流预测能力不足是由于流场中涡黏性过大,为了解决这个问题提出FBM模型。FBM模型在原模型湍流黏性系数的基础上增加滤波器,得到新的湍流黏性系数为
(10)
式中fFBM为滤波函数,由滤波器尺寸Δ和湍流结构尺寸的比值决定,定义为
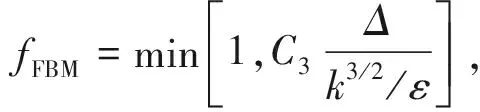
(11)
为了确保滤波与数值方法相容,所选的滤波器尺寸应不小于计算网格区域的大小,即Δ>Δgrid,这里的网格大小定义为Δgrid=(Δx,Δy,Δz)1/3,Δx,Δy和Δz分别为网格在3个坐标方向的长度。
对于湍流尺度小于滤波器尺寸的流动,涡黏保持标准k-ε模型的黏度不变;对于湍流尺度大于滤波器尺寸的流动,由式(11)可知,其湍流黏度变为
(12)
1.3.3 FBDCM模型
Huang等[18]认为FBM模型没有正确修正近壁的涡黏,在空穴周围没有相变的区域,FBM模型计算的涡黏仍然过大。考虑到水翼绕流的动态特性,可以将空化区分为附着空穴和分离空穴两个子域。在附着空穴区,蒸汽的相对体积分数较高,可以看成可压的两相流。在分离的空穴区内是大尺度的气液混合不稳定运动,需要将当地的湍流结构尺寸考虑在内。由此,Huang等在FBM模型的基础上,结合Coutier-Delgosha等[19]提出的用流场的当地密度代替平均密度的DCM模型,提出了FBDCM模型。与FBM模型类似,只对涡黏项进行了修正
(13)
(14)
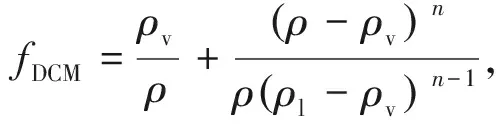
(15)
式中χρ/ρl用来加权两种模型的滤波函数,定义为
(16)
式中:C1=4;C2=0.2。
1.3.4 MFBM模型
洪锋等[20]认为,将FBM模型和DCM模型的滤波函数相互比较后得到的MFBM模型可以兼具两种模型的优点,则MFBM的湍流黏度系数为
(17)
fMFBM=min(fFBM,fDCM)
(18)
1.4 数值计算
本文以二维Clark-Y型水翼作为研究对象,翼型的弦长c=70 mm,攻角α=8°,空化数σ=0.8,计算域的几何参数如图1所示。边界条件设置采用速度入口条件,流速V∞=7.8 m/s,湍流强度I=2%;出口为压力条件,利用空化数可以推导出口的压力值;上下壁面及水翼壁面均设置为无滑移壁面。计算介质采用25 ℃的水和水蒸气,饱和蒸汽压为3 574 Pa。本文的实验数据来自文献[10]。数值计算平台为ANSYS CFX 15.0。
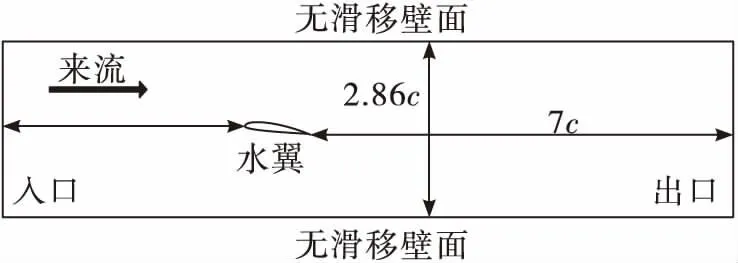
图1 计算域几何示意图Fig.1 Geometric diagram of computational fluid domain
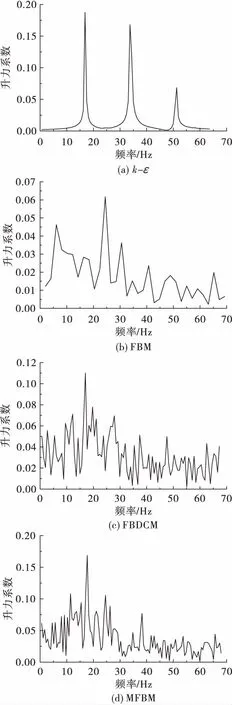
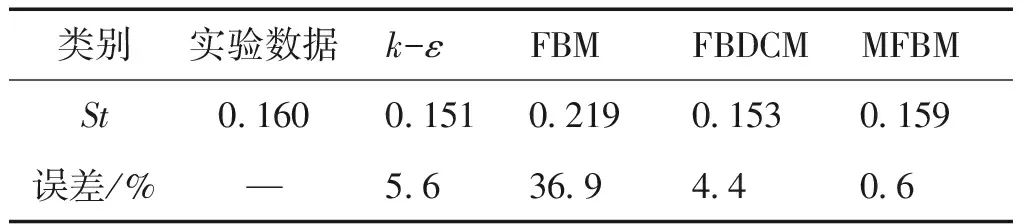
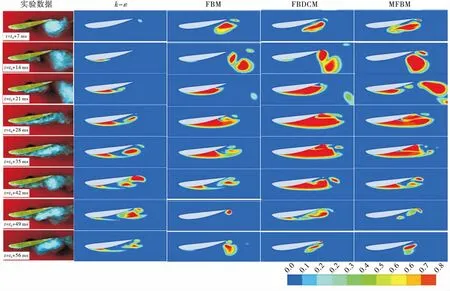
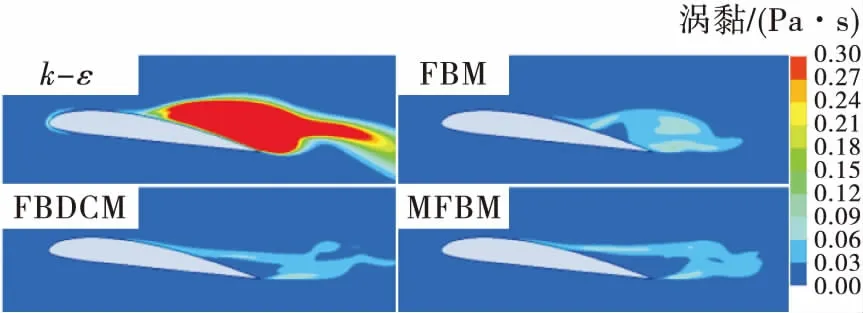
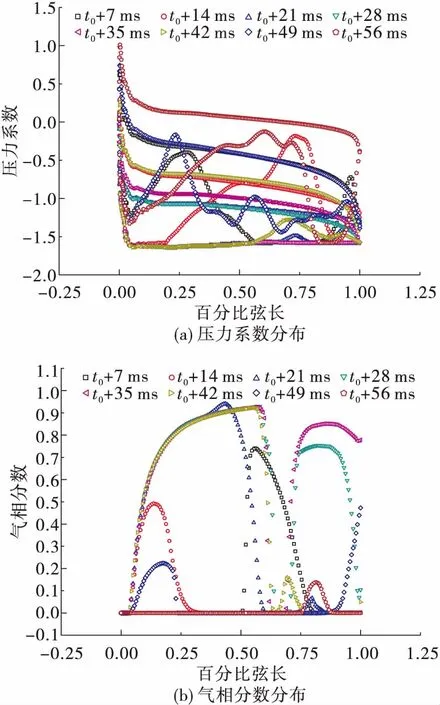
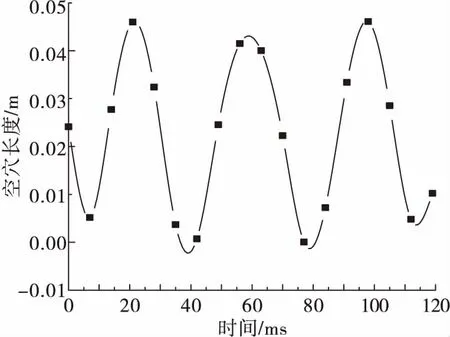
首先利用标准k-ε模型计算绕二维水翼的定常空化流动来验证网格无关性。本文共验证了5套网格,网格数分别为77 056(mesh1)、144 770(mesh2)、187 524(mesh3)、213 512(mesh4)和275 667(mesh5),水翼附近采用O型网格划分,并对靠近壁面的网格进行加密,结果显示30 利用这5套网格计算水翼在定常空化状态下的升力系数 (19) 式中:Clift为水翼的升力系数;Flift为水翼表面的升力;V∞为无穷远处的速度;S为参考面积。 在不同网格下计算的升力系数与实验数据对比如图2所示。 从图2可以看出,mesh2的误差是最小的,但只有在网格数量大于187 523(mesh3)后,计算结果不随网格数改变而改变,说明mesh2的小误差只是偶然的,不能作为最终的计算网格。mesh3计算的升力系数与实验数据的误差小于5%,满足了网格无关性的要求。为了节省时间和计算资源,本文选用mesh3作为最终的计算网格,如图3所示。 图2 仿真计算的升力系数与实验数据的对比Fig.2 Comparison of calculated lift coefficient with experiment data 图3 计算网格Fig.3 Computational grids 2.1.1 翼型升力系数的对比 图4是4种不同湍流模型计算水翼空化得到的基于升力系数的FFT变换。从4张图中均能看出比较突出的主频,表明这里的4种湍流模型都能够捕捉该工况下的非定常流动特性。但标准k-ε模型的FFT变化与其他3种模型明显不同,除了能够分辨主频,次频也很明显,主频与次频之间不存在其他杂频。对于其他3种修正模型,虽然主频也很明显,但几乎无法分辨次频,主频附近分布许多小杂频,表明修正的湍流模型显著增强了计算结果的非定常性。 将4种模型的计算结果与实验数据进行对比,如表1所示,其中基于弦长的斯特劳哈尔数 (20) 式中f为升力系数变化的频率。 图4 关于升力系数的快速傅里叶变换Fig.4 Fast fourier transform of lift coefficient around hydrofoil 表1 不同湍流模型计算的St与实验数据的对比 从表1可以看出,只有FBM模型的St要大于实验值,即升力变化周期要小;而标准k-ε模型、FBDCM模型和MFBM模型的St要小于实验值,即升力变化周期要长一些。4种湍流模型中标准k-ε模型的St是最小的,其他3种模型的St都大于0.151,说明修正模型的非定常性更加突出。在3种修正模型中,FBM模型的St过大,误差高达36.9%,效果反而不如标准k-ε模型;FBDCM模型和MFBM模型的St与实验数据较为吻合。MFBM模型的St是最接近实验值的,与实验数据的误差不到1%,在4种湍流模型中能够更好地捕捉流动的非定常特性。 2.1.2 空穴形态的对比 图5给出了4种湍流模型计算的空穴形态与实验数据的对比。从图5中可以看出绕水翼空化由两部分组成,头部的附着空化和尾部的脱落空化。标准k-ε模型的空穴形态在长度和厚度以及脱落空化的面积上都与实验存在较大的误差,即使在空穴发展最充分的阶段(t0+28 ms),标准k-ε模型的部分空化长度刚刚超过弦长的一半,而实验数据则显示空穴覆盖了整个吸力面,反映出标准k-ε模型在预测非定常空化流动时存在较大的缺陷。3种修正湍流模型采用相同的滤波尺寸进行计算,在空穴形态的预测上有较大的改进,模拟出的空化附着部分长度、厚度增加,脱落部分的空化也更为明显。修正模型中,FBM模型的改进效果是最不明显的,在空穴区变化周期的中间阶段(t0+21 ms~t0+42 ms),附着空化最长可以发展到水翼吸力面3/4的位置,但没有产生超空化;FBDCM模型的空穴在3种修正湍流模型最长最厚,特别是在t0+28 ms和t0+35 ms两个阶段,比实验数据显示的空化区域还要大,是FBDCM模型的不足之处;MFBM模型仿真的结果是最为接近实验数据的一组结果,空穴区的发展形态以及脱落后与实验数据相比都能一一对应。FBM模型以滤波尺寸为界限,没有修正小于滤波尺寸网格内的涡黏,而FBDCM模型和MFBM模型在此基础上从不同角度修正了翼型近壁区的流场,是对全流场的修正,因而后两种模型能更好地捕捉空化的非定常流动特性。从计算结果来看,MFBM模型的效果是最佳的。通过模型的控制方程分析,MFBM模型中,小于滤波器尺寸的近壁区网格用DCM模型计算,而近壁区的流动是非定常性较强的区域,伴随着相变和密度的变化,DCM模型中用当地密度代替平均密度进行计算是较为合理的。 图5 不同湍流模型计算的气相分数云图与实验数据的对比Fig.5 Comparison of vapor volume fraction contours calculated by four turbulent models with experimental data 2.1.3 流场涡黏系数的对比 涡黏系数跟流动非定常性直接相关,标准k-ε模型的涡黏系数与湍动能k与湍动能耗散ε直接相关,无法准确模化湍动能与湍动能耗散导致标准k-ε模型预测非定常流动效果不佳。为了分析不同湍流模型对非定常流动预测能力差异形成的原因,图6给出了4种湍流模型计算的流场涡黏。从图中可以看出标准k-ε模型水翼吸力面后半部分以及尾迹区的涡黏都非常大,这势必会影响模型预测非定常流动的准确性,使得仿真结果出现较大的误差。3种修正模型则大幅减小了流场的涡黏系数,这是修正模型能够更好地预测非定常空化流动的重要原因。由于流动的非定常特性得以凸显,用修正模型计算得到的结果会在真值附近出现较大的波动,所以在图4的FFT变换中,修正模型的频域图中除了突出的主频还伴随着许多小杂频。3种修正模型中,FBM模型计算的涡黏是最大的,因为没有修正近壁处的流场;FBDCM模型和MFBM模型计算的涡黏非常相近且略小于FBM模型,实际上这两种模型计算得到的基于升力变化的St也非常相似,与涡黏云图的结果是一致的。 MFBM模型能够更好地预测非定常空化流动特性,标准k-ε模型是在代数涡黏模型的基础上发展起来的,它和代数涡黏模型的主要区别在于标准k-ε模型的涡黏系数包含部分历史效应[16],MFBM模型作为标准k-ε模型的延伸,修正了涡黏过大对于流场仿真结果的影响,但并没有改变湍动能和湍动能耗散的生成。因而,MFBM模型虽然可以更好地预测空化流动的非定常特性,但MFBM模型仍然无法准确预测湍流统计量关系之间的历史效应,导致仿真结果与实验存在一定误差。虽然MFBM模型结合了FBM模型和DCM模型来修正近壁区流场,但只是在计算中选择使当地涡黏更小的滤波系数进行模拟,物理依据上有所欠缺。如果能在FBM模型的基础上更科学地修正小于滤波尺寸网格的区域,还可以更加准确地捕捉非定常流动的特性。 图6 不同湍流模型计算的涡黏Fig.6 Eddy viscosity calculated by four turbulent models 2.2.1 逆压梯度的对比 图7是一个周期内水翼表面压力系数与气相体积分数分布图。图7(a)中水翼吸力面的低压区的长度和位置与图7(b)中空穴的长度和位置一一对应,头部的低压区对应附着空化,尾部的低压区对应脱落的空化。空化初生(t0+7 ms)时,在吸力面的后半部分有一段长度为0.3c的空穴,是还没有完全溃灭的脱落空化,在0到0.3c的区间存在逆压梯度。随着时间的发展,t0+14 ms时,尾部的脱落空化已经消失,初生的空穴区后0.2c到0.7c的区间内存在较强的逆压梯度,说明伴随着脱落空化的溃灭逆压梯度被增强。t0+21 ms时,脱落空穴的影响基本消失,逆压梯度强度减小,仅在吸力面0.75c的位置存在一个非常小的逆压梯度,附着空化得以进一步发展,空穴长度达到0.7c。此时部分空化脱落较少,逆压梯度对空穴生长的限制作用不明显,吸力面空化会进一步生长成为超空化,从图7(a)图和图7(b)中可以看出t0+28 ms和t0+35 ms时,翼型吸力面被空化覆盖,表面也不存在压力梯度。超空化后,空化开始大量脱落,不断溃灭形成的局部高压区再次加强逆压梯度,逆压梯度又会阻碍空穴生长,促进空化脱落,直到水翼表面的空穴消失,从t0+42 ms到t0+56 ms的3个时间段,逆压梯度位置不断向上游移动,强度也不断增加,直至空穴完全脱落消失。以上的变化说明在一个周期内,空穴的生长和脱落受逆压梯度强度和位置的影响,而空穴的生长与脱落又影响着水翼表面的压力分布。因而,翼型升力变化的周期与空穴的脱落周期是对应的。 图7 水翼表面升力系数与气相分数分布Fig.7 Distribution of lift coefficient and vapor volume fraction around hydrofoil 图8给出了空穴长度随时间的变化。可见水翼表面的空化存在周期性脱落,脱落的周期为40 ms~50 ms,与升力变化周期56 ms[6]基本吻合,表明空化云周期性脱落是升力系数周期性变化的原因,这与前文中分析的结果是一致的。 图8 空穴长度随时间的变化Fig.8 Change of cavity length with time 2.2.2 反向射流的对比 图9给出了一个周期内翼型表面的速度矢量分布。可以看出翼型吸力面头部速度最大,尾部速度最小并伴随回流区。根据伯努利原理,水翼吸力头部速度较大。随着流体沿着翼型向下游运动,逆压梯度会使流动出现分离,形成反向射流。t0+7 ms时,上一个周期的空化还未完全脱落,压力分布上翼型表面存在较大的压力梯度,速度分布上从图9中可以看到在吸力面0.3c到尾部之间存在较强的回流区。t0+14 ms时,回流区移动到翼型尾部,即将脱离水翼,新周期的空化已经初生。t0+21 ms时,随着逆压梯度的消失,回流区大部分消失在主流中,附着在翼型表面的回流区面积大大减小。t0+28 ms和t0+35 ms时,逆压梯度作用不明显,回流区面积基本没有增加,使得部分空化发展成为超空化。在此之后,t0+42 ms时空穴充分发展,尾部的空化与回流区开始相互干涉。回流增强了空化的脱落,脱落空化溃灭瞬间的局部高压造成的逆压梯度又加强了回流,使得回流区的长度和厚度开始增加。另一方面,空化溃灭后反向射流会迅速填满空泡破裂后的间隙,使得回流沿翼型向上游运动,进一步扩大回流区的范围。t0+49 ms时,随着回流厚度不断增加,反向射流已经运动到水翼的头部,与空化区气液交界面相互作用,造成空化云的大尺度脱落,完成空穴在一个周期内的变化。对比图7,反向射流的位置与逆压梯度出现的位置是一一对应的,说明反向射流和逆压梯度共同影响空穴的生长与脱落。 图9 水翼表面速度矢量分布Fig.9 Velocity vectors distribution around hydrofoil 本文采用标准k-ε模型和3种修正湍流模型对二维Clark-Y水翼空化流动进行计算,通过仿真结果的相互比较及与实验结果的对比,得出以下结论: 1)与标准k-ε模型相比,修正的湍流模型可以大幅减小流场中的涡黏,使得雷诺应力的部分历史效应得以凸显,从而增强模型对于非定常空化流动的预测能力。 2)MFBM模型在3种修正模型中,捕捉的非定常空化流动特性与实验最为接近,效果最好,能够比较有效地模拟二维水翼非定常空化流动。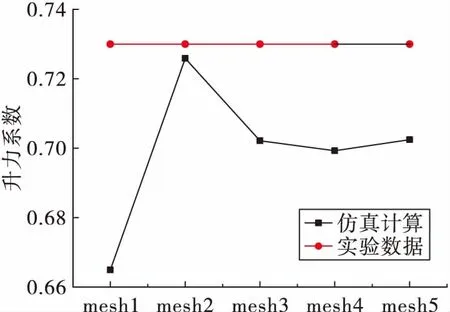

2 结果与讨论
2.1 仿真结果比较
2.2 水翼非定常空化流动分析

3 结论

