基于导叶端弯的小展弦比燃气涡轮优化设计

毛 凯，李昌奂，张 聃，蒋建园

(西安航天动力研究所，陕西 西安 710100)

0 引言

涡轮损失主要包括叶型损失、二次流损失以及间隙泄漏损失，对于小展弦比涡轮，二次流损失是涡轮叶栅通道损失的主要组成部分，约占总损失的30%～50%。控制好二次流损失对于提高小展弦比涡轮效率意义重大。根据二次流损失来源及产生机理，王仲奇[1]提出一种重要的弯曲叶片理论，通过选择叶片在端壁的倾角，合理组织低能流体的流动达到降低二次流的目的，目前叶片端弯设计已经成为减小二次流损失的重要设计方法[2-3]。为了探索端弯叶片对流场的影响，科技人员进行了大量研究，文献[4]研究了不同类型的弯曲叶片，对小展弦比涡轮进行了数值仿真，结果表明正弯设计能有效降低上端区的损失，最大降幅接近5%。文献[5]中采用CFD的方法对小展弦比涡轮进行了导叶正弯和J弯设计，结果表明对于跨音速微型轴流涡轮，正弯流动损失明显比J弯大。文献[1]采用试验的方法对弯叶片进行研究，试验表明，t/L=0.685，H/L=0.68，端部倾角为10°，20°时弯叶片的损失系数比直叶片分别减少了32.3%和41.1%。

对于补燃循环火箭发动机，涡轮通常处于富氧环境中，高可靠性要求动叶叶顶具有足够大的间隙[6-8]，通常不小于5%，间隙泄漏损失对涡轮总体性能影响很大。为了降低间隙泄漏损失，除了采用较复杂的密封结构外[9-12]，还需从根本上优化导叶出口压力径向分布，减小叶顶泄漏通道前后压差。

因此，为了减小端壁二次流损失、改善导叶和动叶通道内部流动、优化导叶出口压力径向分布，本文对某型火箭发动机涡轮导叶进行了优化，通过调整导叶子午端面型线曲率以及导叶端弯设计的方法，显著改善了涡轮内部流场，减低了泄漏损失，提高了涡轮效率。

1 研究对象

本文研究对象为某型发动机用亚声速涡轮，采用小静叶出口角、小展弦比设计方案，结构上采用叶栅式喷嘴、带叶冠式动叶、壳体上设置较复杂的迷宫齿结构，导叶和动叶均为等截面拉伸直叶片，子午面为圆柱形通道，主要设计参数见表1。

表1 涡轮设计参数

2 优化改进思路

2.1 子午面端壁线优化

基于完全径向平衡方程[13]，有

(1)

式中：ρ为密度；p为当地压力；r为半径；Vu为周向速度；Vm为子午速度；φ为斜率；rm为曲率。

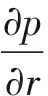
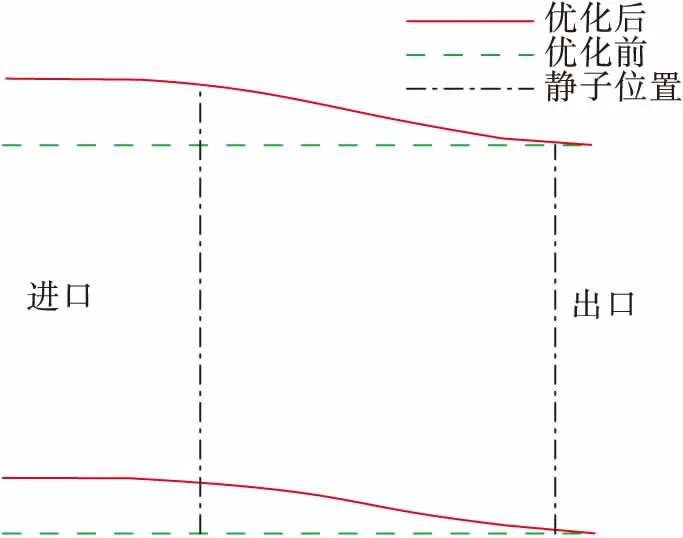
图1 子午面型线优化Fig.1 Optimization of meridional endwall

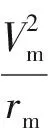
2.2 导叶端弯设计

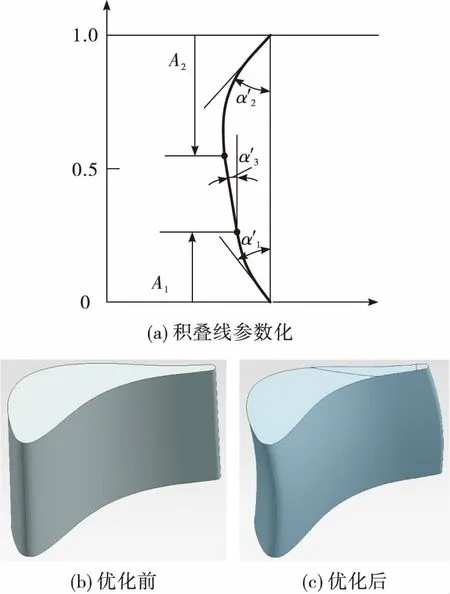
图2 积叠线及三维造型对比Fig.2 Stacking line and 3D model comparation

3 数值计算方法

3.1 计算模型

进行了两种模型计算，case1不考虑动叶与壳体间隙泄漏，采用单通道计算，其主要目的是对优化前后结构叶片通道区域流场进行计算，对比优化前后流场特性的变化，只考虑叶栅通道的损失，计算得到的效率为涡轮轮周效率。case2包含壳体上的迷宫结构，考虑涡轮泄漏损失，采用全通道计算。叶片通道及迷宫结构如图3所示。

图3 叶片通道及迷宫结构Fig.3 Blade passage and maze structure

3.2 网格离散

case1和case2叶片通道均采用结构化六面体网格，使用Autogrid5软件进行网格划分，拓扑结构O-4H形，壁面进行加密处理。case2中迷宫流域采用非结构化六面体网格。case1总网格数为200万左右，case2总网格数1 800万左右。网格划分如图4所示。

图4 叶片通道及叶顶间隙网格划分Fig.4 Mesh of blade and maze clearance

3.3 数值计算方法

数值计算采用CFX软件，对三维雷诺平均Navier-Stokes方程进行求解，方程的离散采用二阶格式。采用标准的两方程k-ε湍流模型，近壁区采用壁面函数法。导叶和动叶之间采用“动静交界面模型”。计算工质采用理想燃气。

4 仿真结果分析

4.1 涡轮总体性能

表2给出了两种计算模型优化前后涡轮总体性能对比。从表中可以看出，单通道不带间隙计算模型优化后涡轮效率提高1.4%，考虑叶顶泄漏后，优化后效率提高5.9%。文中涡轮效率均为扭矩效率

(2)

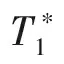
表2 涡轮总体性能

4.2 流动分析

图5和图6给出优化前后导叶吸力面极限流线和压力分布(case1模型)。从图中可以看出，原型和优化后导叶整个叶片表面极限流线基本平行于端壁，流场稳定，无漩涡结构。受通道涡及二次流的影响，原型叶片叶顶和轮毂处的流线在叶片中游区域开始向径向偏转，优化后结构该偏转开始位置向叶片上游发展。

图5 导叶表面极限流线(吸力面)Fig.5 Extra streamline of vane (suction surface)

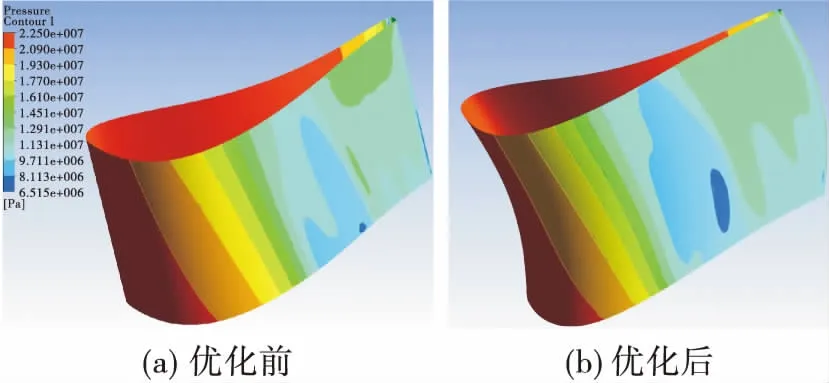
图6 导叶表面静压分布对比Fig.6 Pressure contour of vane

从图6中可以明显发现，优化的正弯叶型导致在叶背形成了“C”型压力分布，叶片中部静压下降，导致上下端区低能流体向主流区域迁移，使得上下端区损失下降，主流区损失增加。

定义压力系数Cps，总压损失系数ζt如下

(3)

(4)

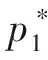
图7给出了导叶出口(110%轴向位置)总压损失系数沿展向分布，可以看出，结构优化后，靠近端面附近总压损失减小，尤其是在轮毂附近改善明显，主流区域总压损失系数相对增大，但导叶平均总压损失系数在优化前后基本相同。

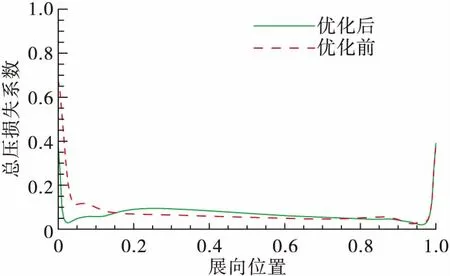
图7 导叶出口总压损失系数沿展向分布Fig.7 Total pressure loss coefficient distribution along span at outlet of vane

图8给出了导叶出口处(110%轴向位置)周向平均压力系数沿展向位置分布，从图8中可以看出与原型结构相比，仅采用子午面型线曲率调整方法(图中对应“子午型线优化”曲线)，叶顶处压力系数降低1.3%，但轮毂处压力系数同样降低，说明子午面型线进行收缩并沿流向下倾改进之后，整体降低了轮毂和叶顶处的压力，降低了间隙泄漏损失，但轮毂处负反力度减小导致轮毂附近流动恶化。在子午面型线调整基础上，进一步采用导叶端弯设计后，轮毂处压力升高，减小了轮毂处负反力度，改善轮毂处流动情况，叶顶压力系数相比较原型降低2%(图中对应“优化后”曲线)。

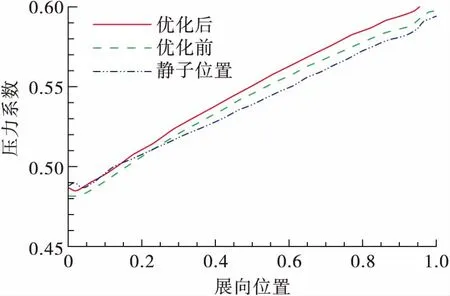
图8 导叶出口压力系数沿展向分布Fig.8 Pressure coefficient distribution along span at outlet of vane

从图9可以看出，优化后叶顶间隙压力高于原型结构。通过提取case2计算模型中叶顶间隙内泄漏量，发现相对泄漏量从原来的7%降低至4.75%，下降了32%。

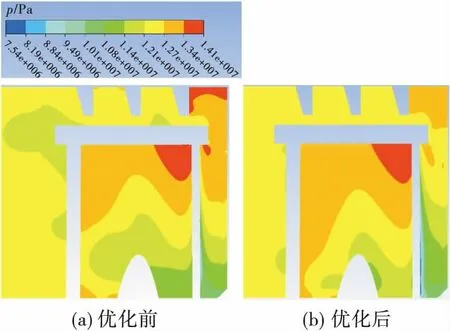
图9 叶顶间隙内压力(右：进口)Fig.9 Pressure contour of blade topclearance

图10给出导叶出口和动叶入口周向平均气流角度沿展向位置分布(α1为导叶出口绝对气流角，β1为动叶入口相对气流角)。从图10中可以看出结构优化后轮毂和叶顶处绝对和相对气流角显著增大，叶中部气流角有所减小，整体分布更加均匀。气流角度分布的变化直接影响动叶入口气流攻角，从图11可以看出，原型在轮毂附近气流正攻角很大，动叶叶背处气流分离。优化后动叶入口相对气流角的增大使得气流与叶型角度匹配更佳，完全消除了原型结构在轮毂附近叶背区域的分离涡，轮毂处气流马赫数明显高于原型结构，减小了轮毂处二次流损失。

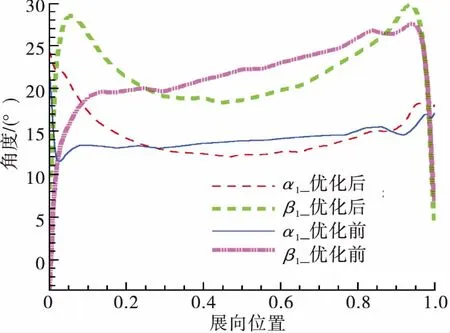
图10 气流角沿展向分布Fig.10 Flow angle distribution along span

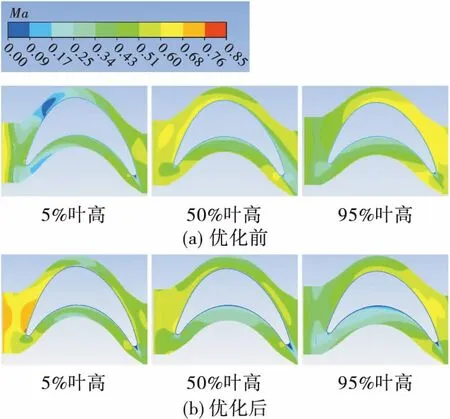
图11 动叶不同展向位置马赫数分布Fig.11 Mach contour at different span of blade

图12给出优化前后动叶吸力面极限流线。由于动叶展弦比低，而且叶片未进行径向三维造型设计(径高比<8)，吸力面轮毂处和叶顶处均有强烈的二次流动，通道涡急剧向叶中发展，在叶片尾缘处基本占据叶高约80%左右。对导叶进行优化后，并未消除动叶通道内的强二次流动。相比较于原型结构，轮毂附近径向流线迁移的起始点明显向叶片下游移动，在叶片尾缘处二次流占据叶高60%左右，一定程度上缓解了端壁二次流动对主流的影响。后续可对动叶叶片进行进一步优化设计。

图12 动叶表面极限流线(吸力面)Fig.12 Extra streamline of blade(suction surface)

5 结论

对某型发动机用亚声速小展弦比燃气涡轮进行了优化，对导叶子午面型线曲率变化进行调整，并对导叶进行正弯设计，通过三维计算仿真分析，得出以下结论：

1)优化后轮毂和叶顶端壁损失减小，主流区损失增大，涡轮效率提高1.4%。

2)采用正弯设计后，轮毂和叶顶处绝对和相对气流角显著增大，叶片中部气流角有所减小，整体分布更加均匀。消除了原型结构动叶轮毂区的流动分离。

3)优化后围带间隙前后压差明显降低，泄漏量从7%降低至4.75%，涡轮效率提高5.9%。