σ2Hessian方程的Pogorelov型C2内估计及应用
缪正武
(浙江工业大学理学院,浙江杭州310023)
0 引言
对任意k=1,2,…,n,定义σk算子如下:
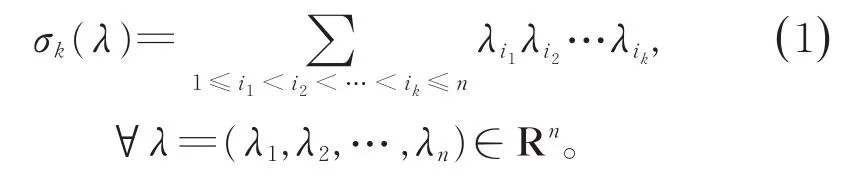
另外,定义σk=0(当k>n或k< 0时),σ0=1。其实σk就是k阶对称多项式。σk算子具有一定的凹性性 质,也 就是在 Ga◦rding 锥 Γk={λ=(λ1,λ2,…,λn)∈ Rn:σi(λ)> 0,1 ≤i≤k}里是凹的,即
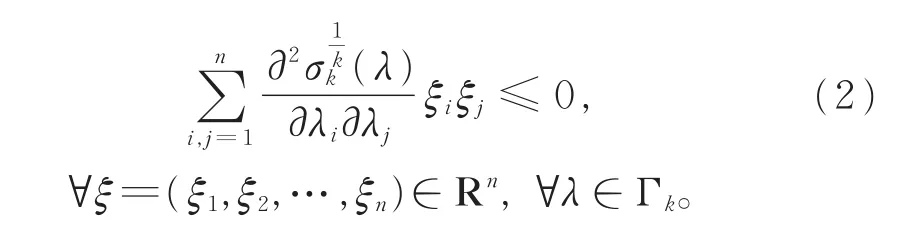
此凹性在σkHessian方程的整体二阶导数估计和解的存在性中具有重要作用。但在建立二阶导数估计时,此凹性对应三阶导数的二次型,而三阶导数满足线性限制条件。因此,应用于σkHessian方程时,此凹性得到了改进。
本文首先利用拉格朗日乘子法重新证明了σ2算子的最优凹性。定义σ2算子对应的二次型为:
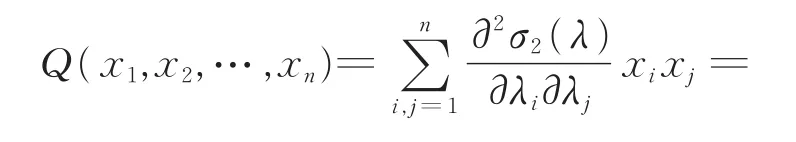
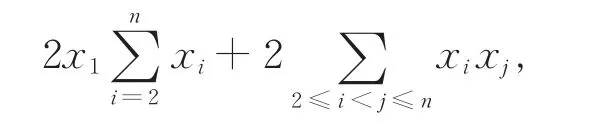
则σ2算子的最优凹性如下:
定理1假设λ=(λ1,λ2,…,λn)∈ Γ2,并且有x=(b,x2,x3,…,xn)∈Rn满足线性限制条件:
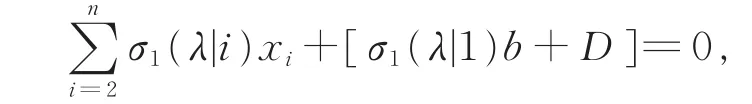
其中b和D为常数。则有
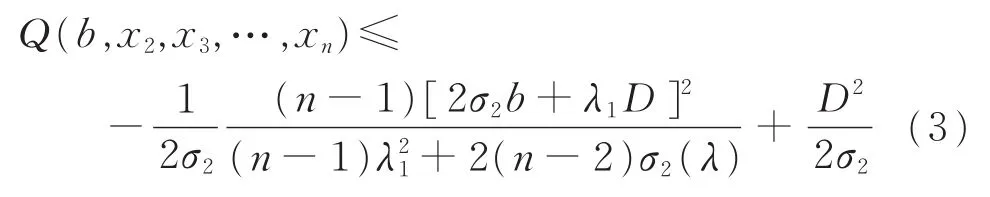
注1定理1是CHEN[1]用特征向量分解的方法得到的。本文利用拉格朗日乘子法重新证明了σ2算子的最优凹性。
注2在某种意义下是最优的,可以推导出式(2)。即对任意ξ=(ξ1,ξ2,…,ξn),令
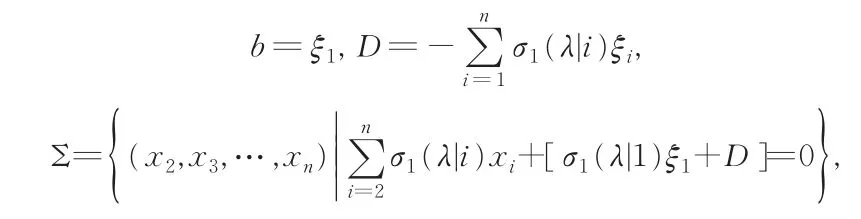
则(ξ2,ξ3,…,ξn)∈ Σ,并且
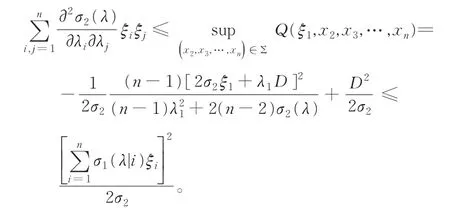
定义锥:
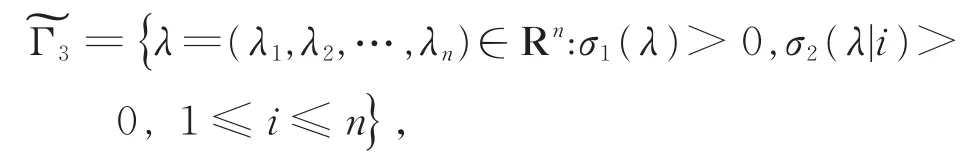
考虑σ2Hessian方程
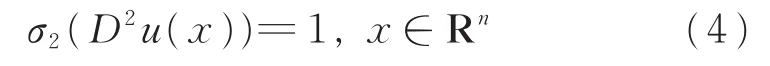
的整解问题。首先BAO等[2]证明了方程(4)的Γ2-凸解u如果满足二次多项式增长条件:
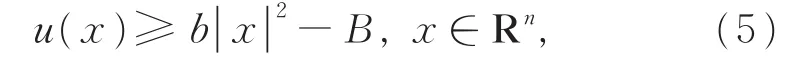
其中b,B为正常数,则解u一定为二次多项式。
YUAN等[3]证明了方程(4)的Γ2-凸解u如果满足半凸条件
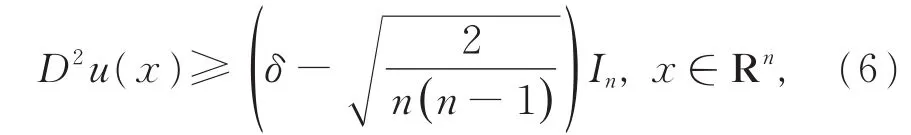
其中δ为任一正常数,则解u一定为二次多项式。
LI等[4]证明了方程 (4)的-凸解u如果满足二次多项式增长条件(5),则解u一定为二次多项式。
定理2设u∈C2(Rn)为方程(4)的-凸整解,并且解u满足二次多项式增长条件(5),则解u一定为二次多项式。
1 准备知识:基本对称多项式的性质
本节将介绍一些文中要用到的基本对称多项式的性质。
定义1对k=1,2,…,n,定义k阶基本对称函数
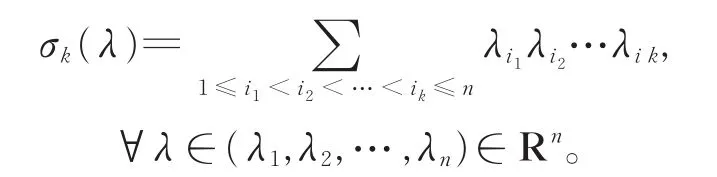
另外,定义σ0=1,当k>n或k< 0时,σk=0。
分别记σk(λ|i)=σk(λ)|λi=0,σk(λ|ij)=σk(λ)|λi=λj=0。
命题1设λ=(λ1,λ2…,λn)∈Rn,k=0,1,…,n,则
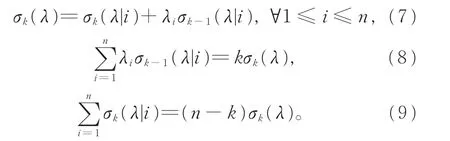
进而可得
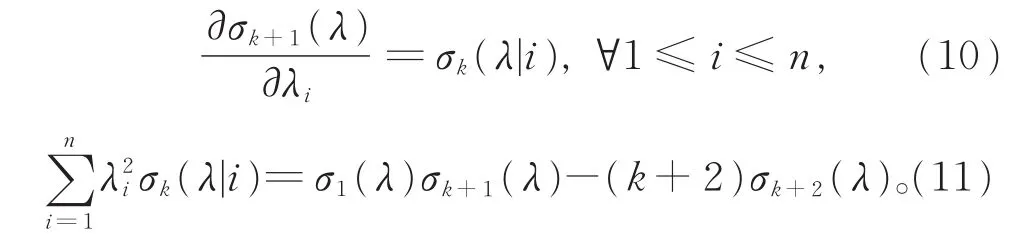
基本对称函数的定义域也可以推广到对称矩阵。
定义2设W为n×n对称矩阵,对k=1,2,…,n,定义
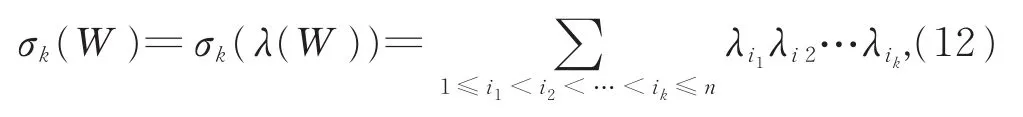
其中λ(W)=(λ1(W),λ2(W),…,λn(W))为矩阵W的特征值。也就是说式(12)为矩阵W的所有k阶主子式的和。
令σk(W|i)表示基本对称函数σk(W)去掉矩阵W中第i行和第i列元素后的值,σk(W|ij)表示基本对称函数σk(W)去掉矩阵W中第i行第j行和第i列第j列元素后的值。
引进Ga◦rding锥的定义如下:
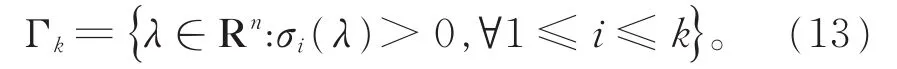
易知Ga◦rding锥Γk是关于λi对称的凸 锥,且Γ1⊃ Γ2⊃ … ⊃ Γn,其中Γn={λ∈Rn:λi>0,∀1≤i≤n}。另外k-阶基本对称函数在Γk上有以下性质:
命题2如果λ∈ Γk,其中k∈ {1,2,…,n},则有σh(λ|i)> 0,∀h=0,1,…,k-1,i=1,2,…,n。(14)
证明见文献[5]。
命题3假设λ=(λ1,λ2,…,λn)∈,n≥ 3,并且

则有
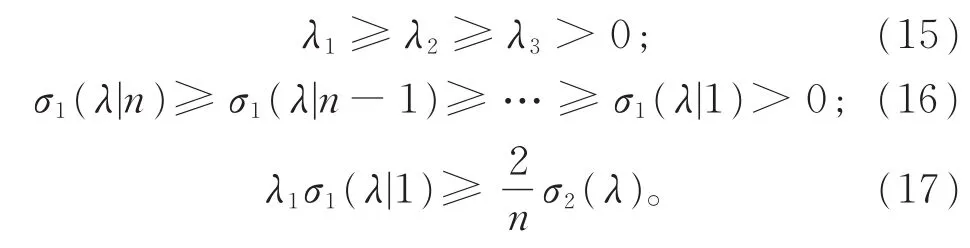
证明由文献[6]可得式(15),由文献[7-8]可证得式(17),直接计算可证得式(16)。
另外下文还要用到对角矩阵的基本对称函数的求导公式。
命题4若W=(Wij)为n×n对角矩阵,m(1≤m≤n)为一正整数,则
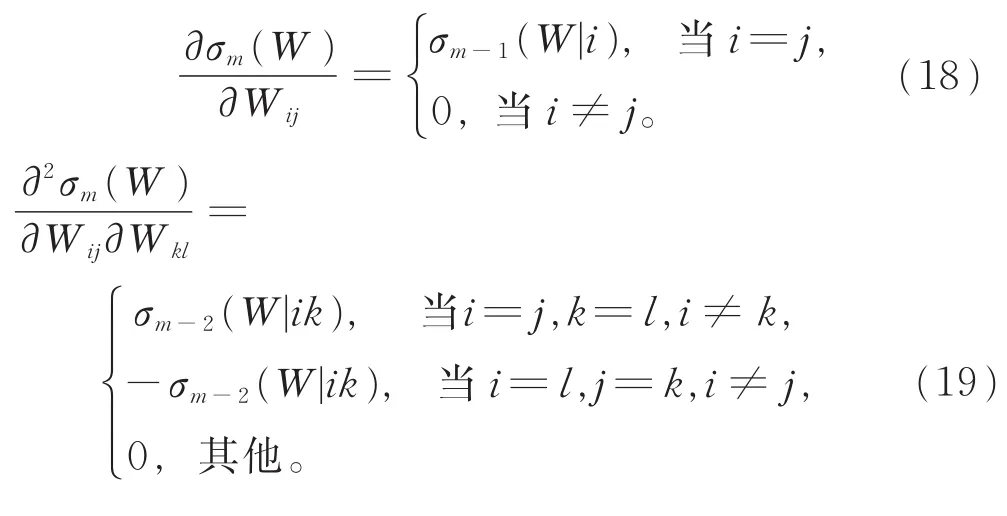
2 定理1的证明
利用拉格朗日乘子法对σ2的最优凹性进行证明。
首先构造拉格朗日函数
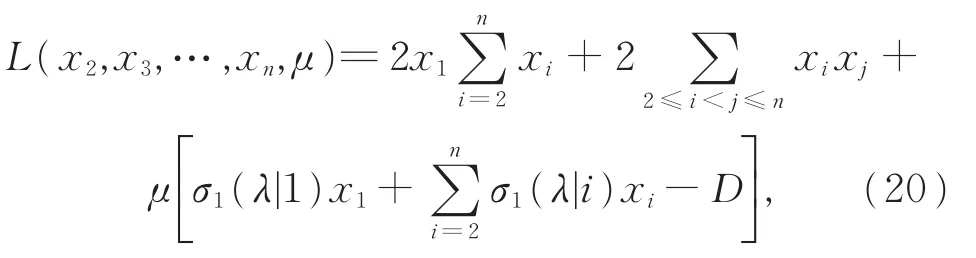
对L求偏导数,并令它们都等于0:
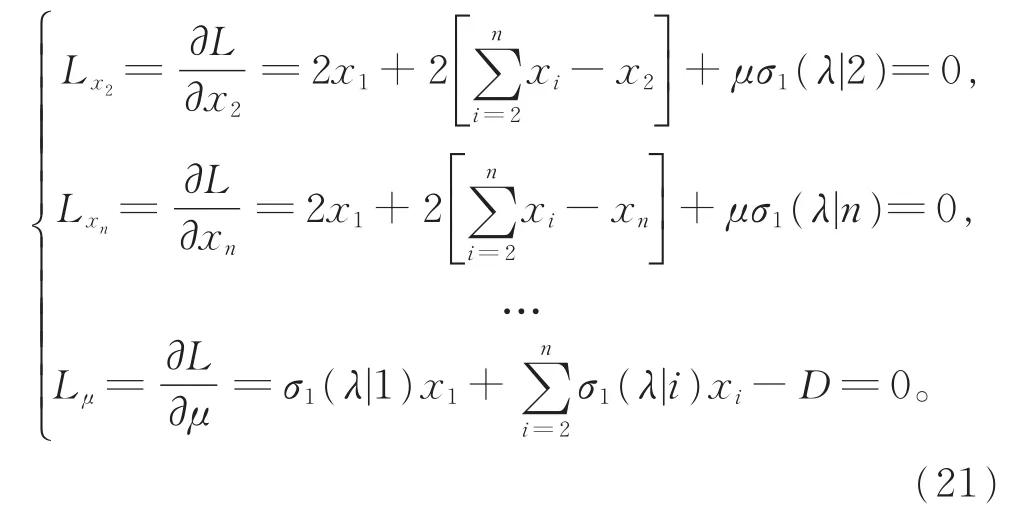
将方程组(21)中的前n-1个方程相加得到:
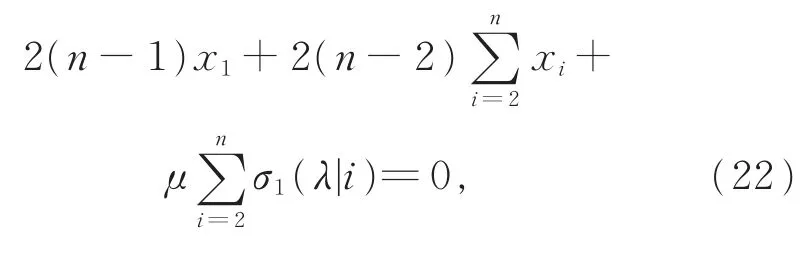
整理得
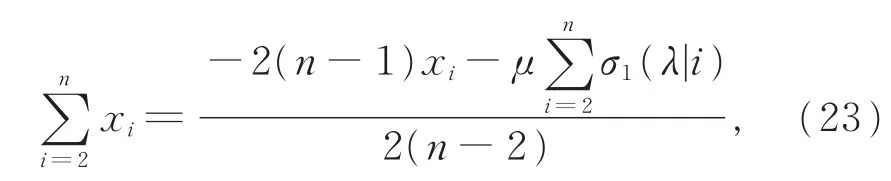
逐式整理方程组(21)中的前n-1个等式,可得
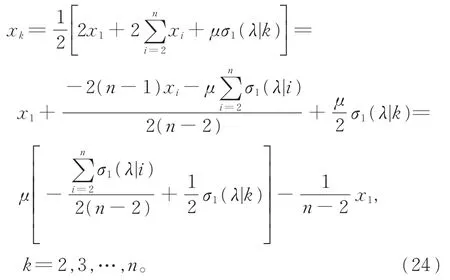
将式(24)代入方程组(21)中的第n个等式,可得
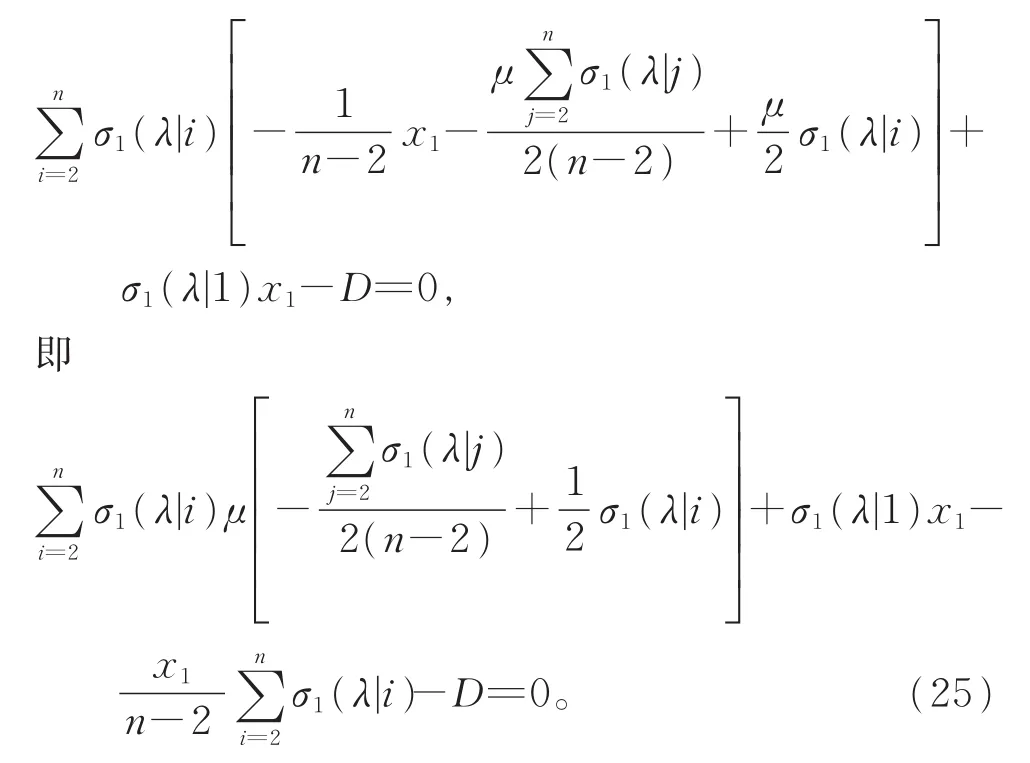
对式(25)反解μ,得到
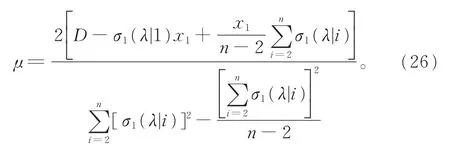
将式(26)中的μ代入式(23),得到

结合式(23)和(24),可得
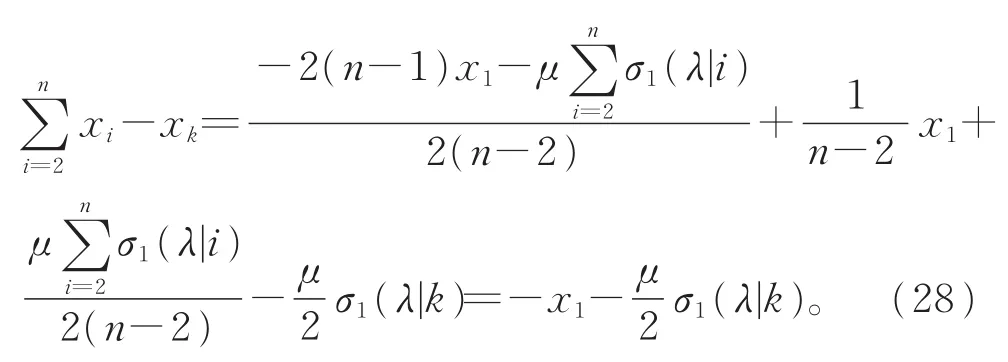
由条件易知所求的稳定点是极大值点,可以验证其是最大值点,因此
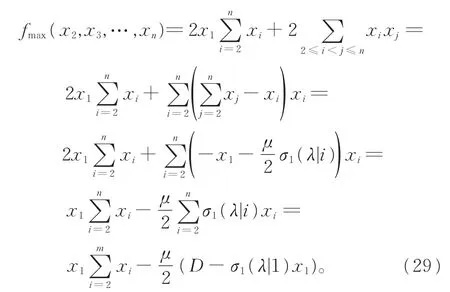
将式(26)和(27)代入式(29),化简得到
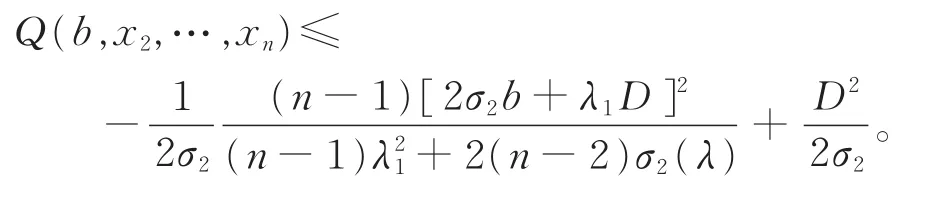
定理1得证。
3 定理2的证明
在证明定理2前,首先给出以下Pogorelov型C2的内估计。
定理3设u∈C4(Ω)为方程
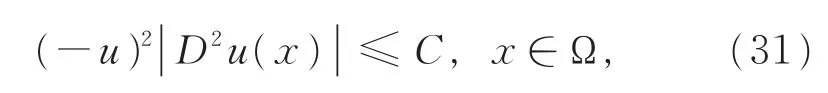
其中正常数C仅依赖n、Ω的直径diam(Ω)和sup|u|。
证明取辅助函数
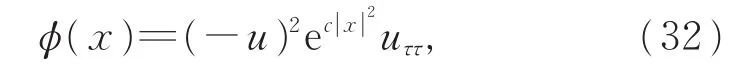
以下假设λi=uii(x0),λ=(λ1,λ2,…,λn)。则辅助函数
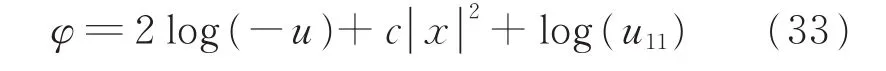
在x0达到局部极大值。
以下计算都在x0点,则有
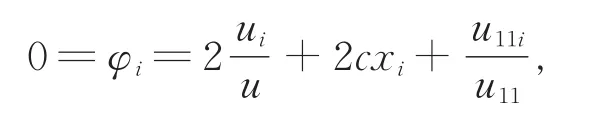
化简得
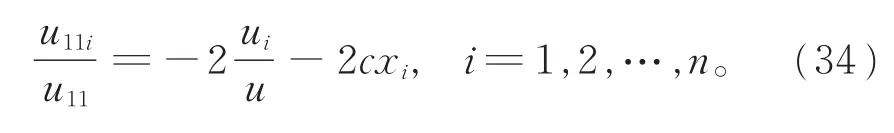
有
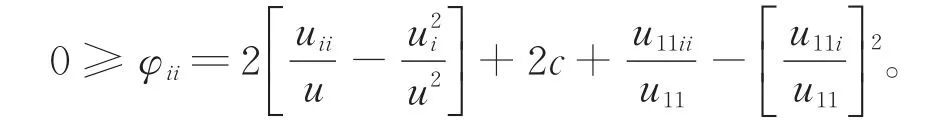
所以有

令
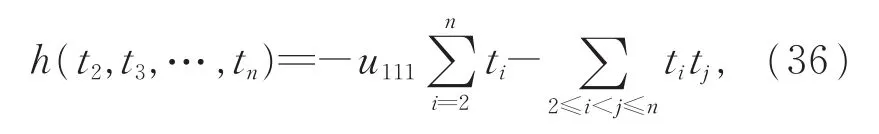
其中ti=uii1。考虑h(t2,t3,…,tn)在线性条件
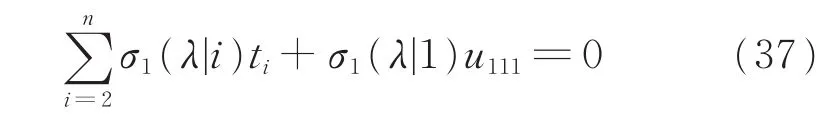
下的最小值问题。由定理1可得
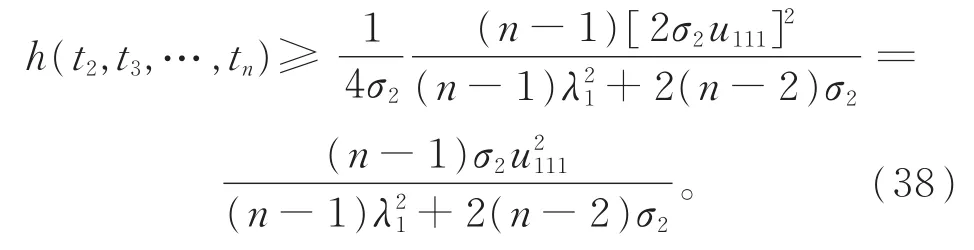
结合式 (35)和(38),可得
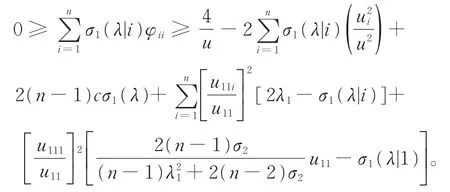
假设λ1≥n+10,由于λ∈易得
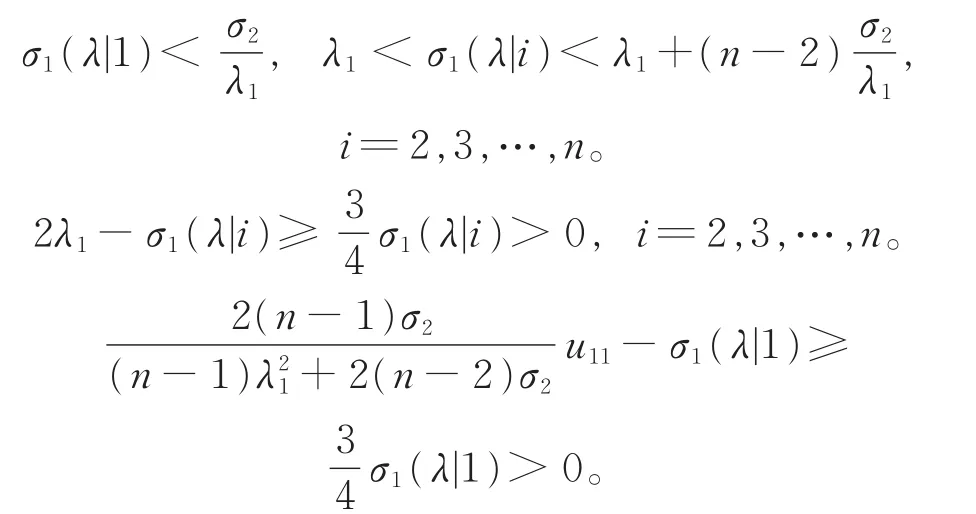
进而可得
所以在x0点,有
在任意x∈Ω点,有
下证定理2。主要思想来自文献[4-9]。
假设u为方程(4)的-凸整解。对任意充分大的实数R>1,定义
则v满足
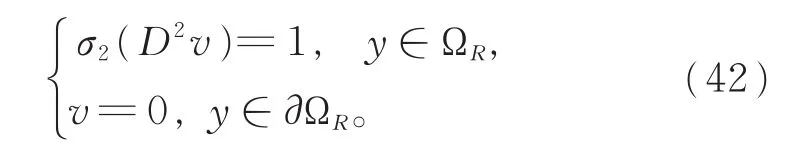
由于u满足二次增长条件,则对任意y∈ΩR,有
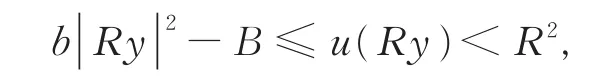
所以

即ΩR对任意的R>1都是一致有界区域。进而由极大值原理可得,在ΩR内-C1≤v≤0,其中C1只依赖于n,b和正常数B。再由定理3可得
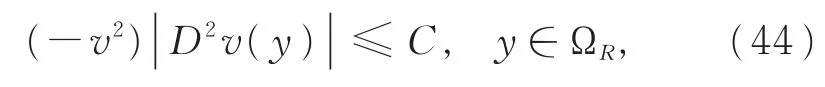
其中,C只依赖于n,b和正常数B,进而可得

而D2v(y)=D2u(Ry),所以令R→+∞,有
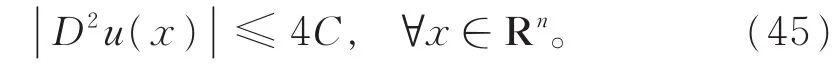
由标准的Evans-Krylov理论[10],可得
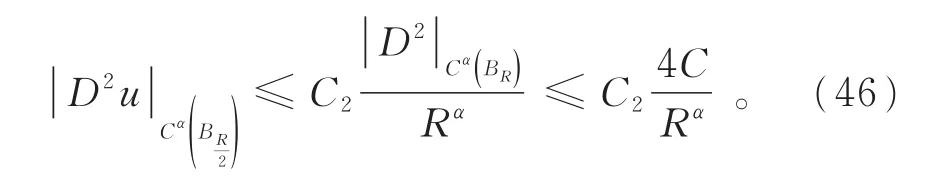
令R→+∞,定理2得证。

