一种提高凝灰质储层渗透率解释精度的方法——以南贝尔油田为例

刘利

（大庆油田有限责任公司呼伦贝尔分公司，内蒙古呼伦贝尔021000）

0 引言

近年来，含凝灰质储层油气藏勘探效果显著，获高产工业油流，成为油气勘探的一个新方向[1]。凝灰质岩作为一种重要的岩石储集类型，在三塘湖、准噶尔、海拉尔-塔木察格、二连等多个盆地均有发育且获得工业油流[2]。渗透率是储层测井评价的重要参数之一，在凝灰质储层中，凝灰质的存在导致储层的孔隙结构和物性发生变化[2]，由于储层非均质性强，利用单一回归分析模型计算的渗透率解释精度较低，因此，研究如何提高渗透率解释精度很有必要。国内外不少学者提出了许多不同的改善渗透率解释精度的途径，如JENNING等[3]提出基于岩石结构系数的广义渗透率模型；BRYANT等[4]提出通过建立精细地质模型预测渗透率；MATHISEN等[5]依据测井曲线特征，用数学统计方法来求解渗透率；廖东良等[6]提出一种用分流动单元计算渗透率的方法。

目前研究区的渗透率解释主要采用的是岩心分析数据与电测曲线的多元回归分析方法，误差较大，难以满足定量评估储层的要求。流动单元是一个流体流动地质和岩石物理性质内部一致的储集岩体，流动单元指数FZI（flow zone inde）是识别流动单元的重要参数。因此，笔者以南贝尔油田为例，采用分流动单元建立渗透率解释模型，将储层测井相关参数与Fisher判别方法相结合判别储层流动单元，并将其推广应用到非取心井，计算其渗透率，以提高凝灰质储层渗透率的解释精度。

1 取心井流动单元划分

1.1 凝灰质对渗透率的影响

研究区南贝尔油田位于塔木察格盆地东北部的南贝尔凹陷，开发目的层位为南屯组一段，主要沉积相为扇三角洲相及滨浅湖相，岩性以灰色凝灰质砂岩、凝灰质砾岩、凝灰质砂砾岩为主，薄片分析表明，岩石主要成分为晶屑、岩屑、火山灰及玻屑，晶屑为石英、长石。岩屑为中、酸性喷发岩，火山灰具重结晶，酸性居多，导致储层段自然伽马较正常储层段明显偏高。孔隙类型以原生的粒间孔隙，次生的粒间、粒内溶蚀孔隙为主。从图1中可看出，凝灰质质量分数的增加导致渗透率总体呈下降趋势。

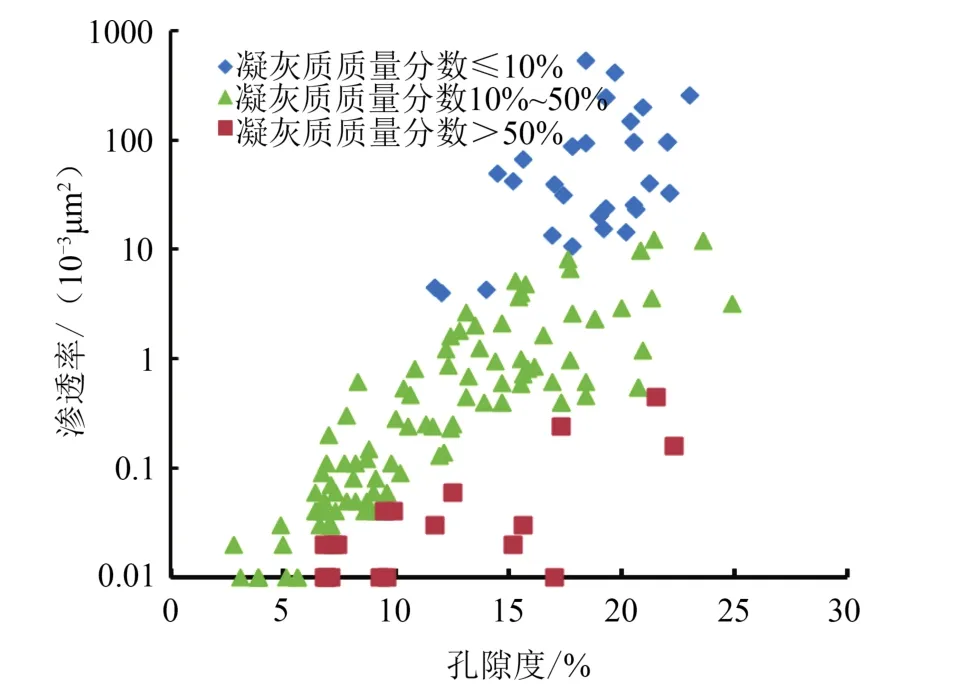
图1 岩心分析孔隙度与渗透率图Fig.1 Core analysis porosity and permeability map

由于凝灰质质量分数增加到50%以上，渗透率下降至1×10-3μm2。南贝尔凝灰质储层的孔隙空间主要以次生孔隙为主，在凝灰质质量分数大于50%时，凝灰质熔结作用强于成岩时期的溶蚀作用，导致渗透率下降。因此，要分类建立其渗透率与孔隙度的关系模型，以提高解释精度。

1.2 流动单元基础理论

流动单元是HEARN等[7]于1984年提出的，定义为横向和纵向上连续的具有相似的孔隙度、渗透率和的储层。流动单元是在岩相划分的基础上对储层的进一步细分，同一流动单元内部相对均质，不同流动单元之间储、渗能力存在较大差异，并有较好的隔挡界面或渗流屏障[6-12]。

流动单元的划分方法主要有：岩石微观孔隙结构法，沉积、成岩、构造作用综合法，沉积学法，露头沉积界面分析法，成因单元与储层物性特征综合法，多参数分析法等[13-14]。岩石微观孔隙结构法有2种：一种是利用Winland方程得到的R35识别划分流动单元，另一种是基于Kozeny-Carman方程推导出的由油藏品质系数RQI、孔隙体积与颗粒体积之比Φz、流动单元指数FZI三者之间的关系来确定流动单元的类别。本文选用的是第2种方法。

运用多孔介质中流体的达西定律与毛管中流体的泊肃叶定律推导的孔隙度与渗透率Kozeny-Caren方程为

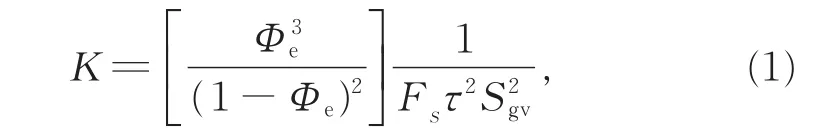
式中，Fs为形状系数 (圆柱体取2)，Fsτ2通 常 称为Kozeny常数，K为渗透率（毫达西），Φe为有效孔隙度，τ为迂曲度；Sgv为颗粒体积单元的表面积（比表面积 μm-1）。

式（1）两边分别除以有效孔隙度Φe后开根号，且将渗透率单位由毫达西转变为10-3μm2，得到

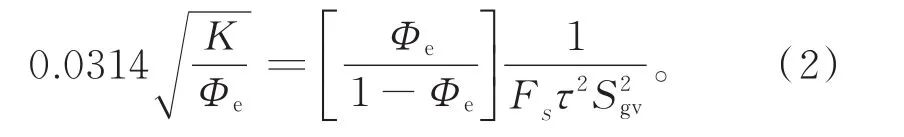
定义油藏品质系数RQI、孔隙体积与颗粒体积之比Φz与流动单元指数FZI如下：

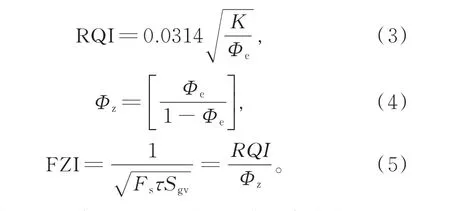
式（4）说明FZI值主要由孔隙度、渗透率决定，可利用此值来划分流动单元。同一流动单元孔隙结构相似、孔隙度和渗透率变化规律相似，但其值不一定一致，所以这些相似孔隙结构的储层其FZI值在累计频率曲线上表现为直线[15-17]。

1.3 岩心流动单元划分

利用南贝尔油田开发区内39口取心井的分析化验数据，统计每一块岩心对应的孔隙度和渗透率，计算其油藏品质因素RQI及流动单元指数FZI，并绘制FZI值累计概率曲线（见图2），可将流动单元划分为Ⅰ、Ⅱ、Ⅲ、Ⅳ 4类，具体分类见表1。

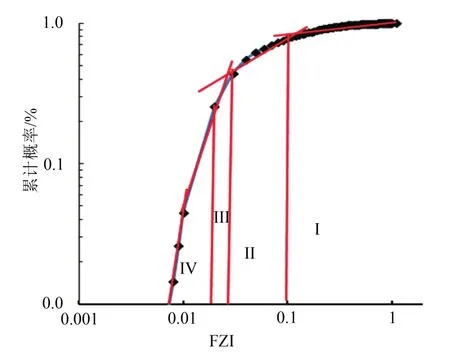
图2 南贝尔岩心FZI值累计概率分布图Fig.2 Nanbeier core FZI value of cumulative probability distribution

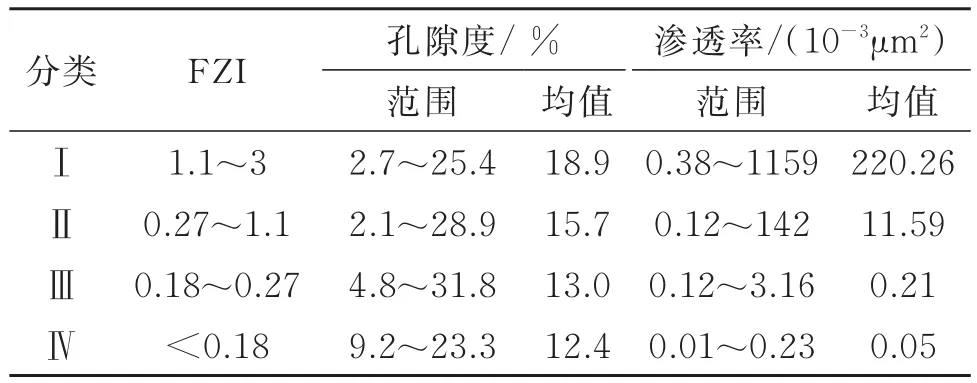
表1 流动单元分类表Table1 Flow unit classification

由于区块的有效厚度下限标准为孔隙度大于9%，渗透率大于0.1×10-3μm2，从表1中可以看出，Ⅰ、Ⅱ、Ⅲ类流动单元为有效储层，Ⅳ类主要为物性夹层、致密层。不同FZI值下的毛管压力曲线分布不同（见图3），Ⅰ类流动的棑驱压力值低，孔吼半径大，随着FZI值的降低，棑驱压力值增大。

表2为分流动单元含油性统计表，从表2的岩心分析数据中可看出，不同流动单元的含油性差异较大，Ⅰ类流动单元基本都是油浸以上级别，Ⅳ类流动单元基本不含油，这也从侧面反映了该划分方法合理可靠。

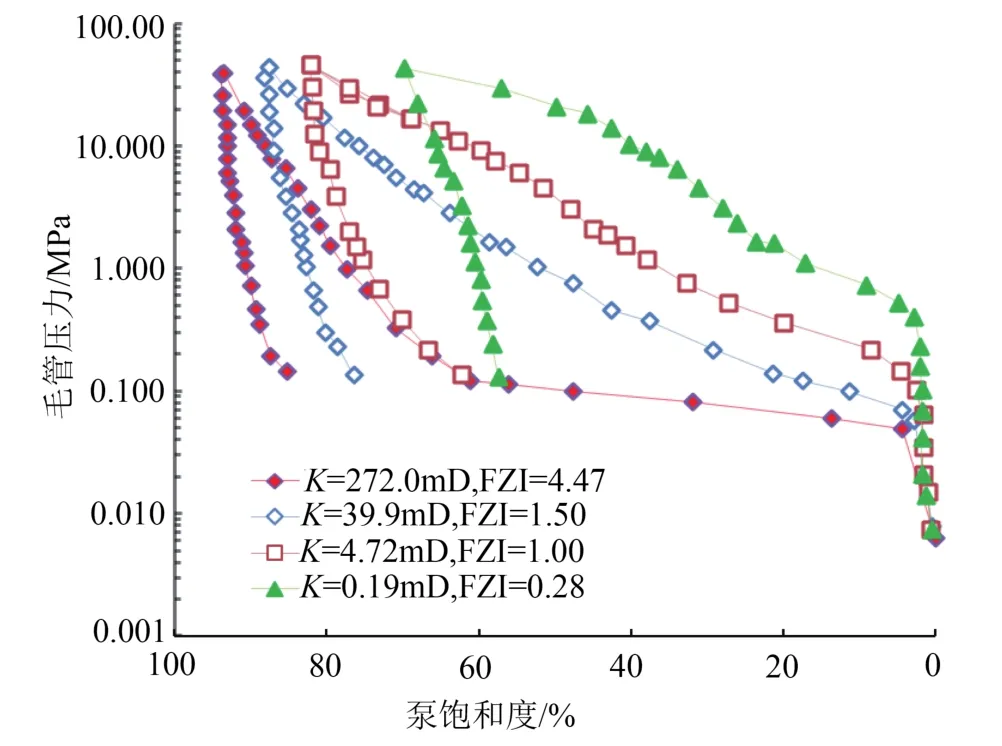
图3 不同FZI值时的毛管压力图Fig.3 Capillary pressure diagram with different FZI values

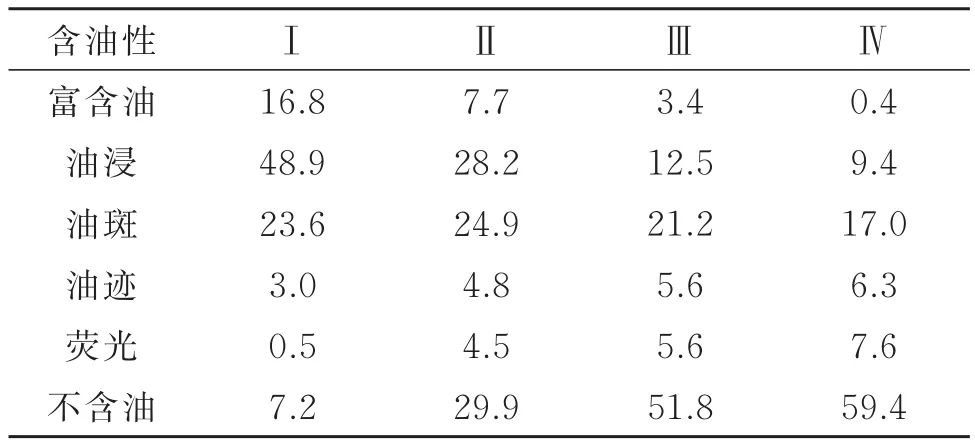
表2 分流动单元含油性统计表Table2 Statistical table of oil content in separate flow units

2 非取心井流动单元划分

2.1 判别分析法

在多元统计中，常用判别分析进行样品所属类型的判定。在研究对象已知时，用某种方法将其划分为若干类，只需确定新样品归属于哪一类。常用的分析方法有距离准则、Fisher准则、贝叶斯准则等[18-19]。

费舍判别分析（Fisher）法是基于统计学的费舍准则，在费舍准则下，确定线性判别函数，判别函数系数的确定原则是使每个分组间区别最大化，且每组内部离散性最小化。有了判别函数后，对一个新的样品，只要将各指标的数值代入判别式，求出y值，然后通过比较分析，便可判别其归属[20-21]。

2.2 储层流动单元划分

选取全区稳定发育的南一段零油组泥岩段作为标志层，对测井曲线进行预处理。选取岩心分析数据密度大于4块/m的层段，每个流动单元类型的样本数大体一致，并通过相关性分析，优选出泥质含量（Vsh）、深侧向电阻率（LLD）及密度曲线（DEN），读取每个层段的曲线参数值，将其作为判别分析的输入训练变量，输出储层流动单元判别函数，其中，泥质质量分数的计算公式为：

式中，GRmin为纯砂岩自然伽马值（API），GRmax为纯凝灰岩自然伽马值（API）；GCUR为地区经验系数，新地层取3.7，老地层取2。

孔隙度采用储量报告提交公式，计算公式为

Φ=0.23×DT-41.80×DEN+95.47,(8)式中，DT为声波时差（us/ft）；DEN为密度（g·cm-3）；相关系数为0.97。

将标准化的测井样本数据作为样本输入SPSS中，选取判别学习数183个，预测样本数100个，得到各类流动单元的判别函数，见表3。由表3得到的Fisher线性判别方程，对没有参加判别学习的岩心点储层类型进行预测，预测正确率达85.1%。

3 渗透率解释模型

利用FZI值对开发区的39口取心井的3 033个岩心样品进行流动单元划分，分流动单元建立岩心分析的渗透率与孔隙度模型，渗透率解释模型见表4。对比划分前后（图4、图5）的数据可知，Ⅱ、Ⅲ类渗透率解释模型的精度有明显提高。

表3 不同流动单元Fisher线性判别方程Table3 Fisher linear discriminant equations for different flow units

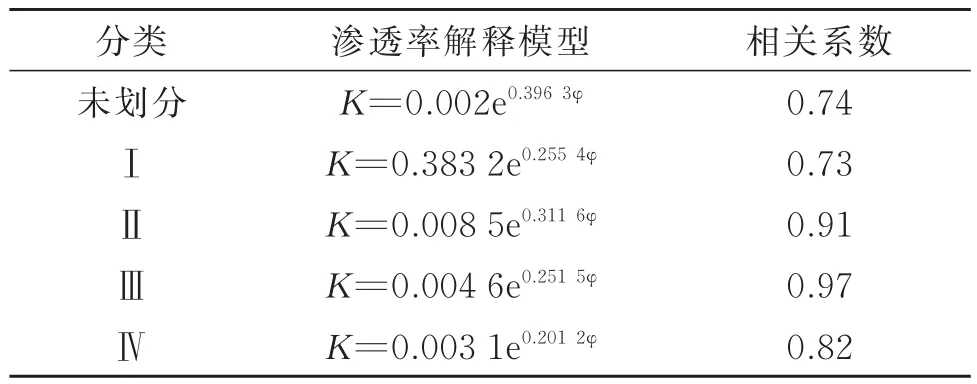
表4 分流动单元渗透率解释模型Table4 Model of permeability interpretation for flow unit

4 应用实例

对研究区39口取心井层段测井曲线进行取值处理，并按照已建立的流动单元判别方程对每个层位的数据进行流动单元识别，然后分流动单元计算对应的渗透率。将分流动单元计算的渗透率与使用常规方法计算的渗透率结果进行对比分析（见图6），从图6中可以看出，分流动单元计算的渗透率与岩心分析结果更接近，相关性更高，而用常规方法计算的渗透率对大于20×10-3μm2的其值明显偏低。从图7的塔02井渗透率计算结果看，右边第3道为采用常规方法时，流动单元计算的渗透率与岩心分析渗透率的对比，可看出分流动单元计算的渗透率更贴近实际岩心分析的渗透率，精度更高。右边第2道为判别分析法划分的流动单元与岩心分析数据计算的流动单元，分类也很吻合。因此，在凝灰质储层中，分流动单元建立渗透率解释模型合理且可靠，可提高解释精度。

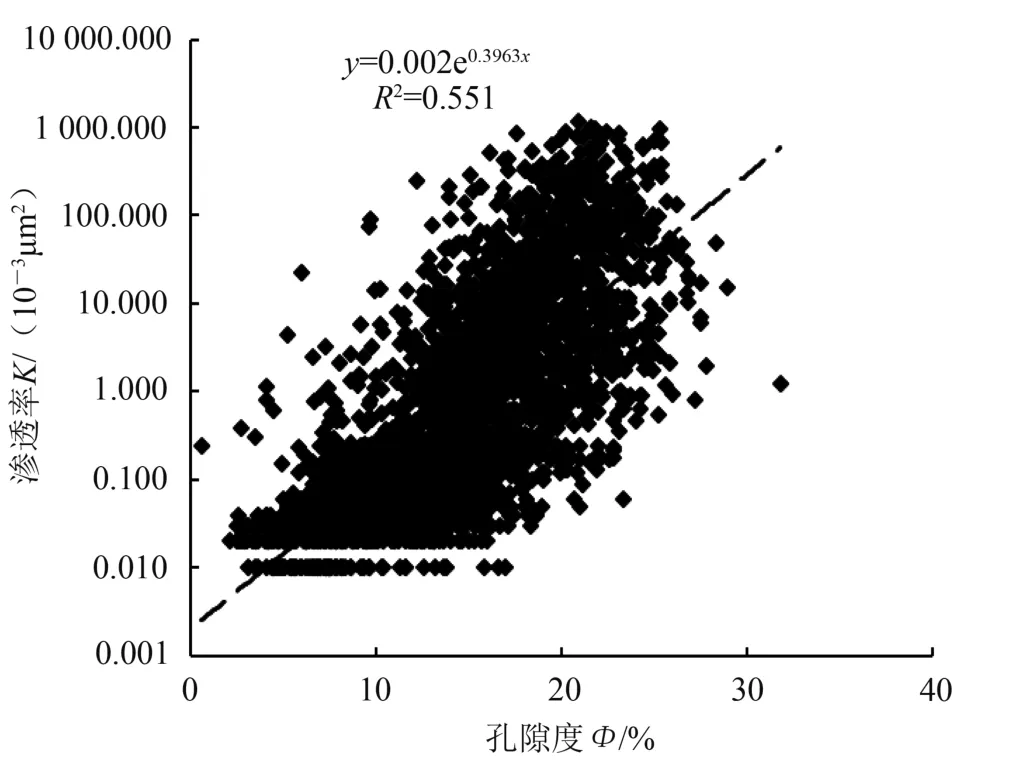
图4 常规方法建立的渗透率模型Fig.4 Permeability model established by conventional method

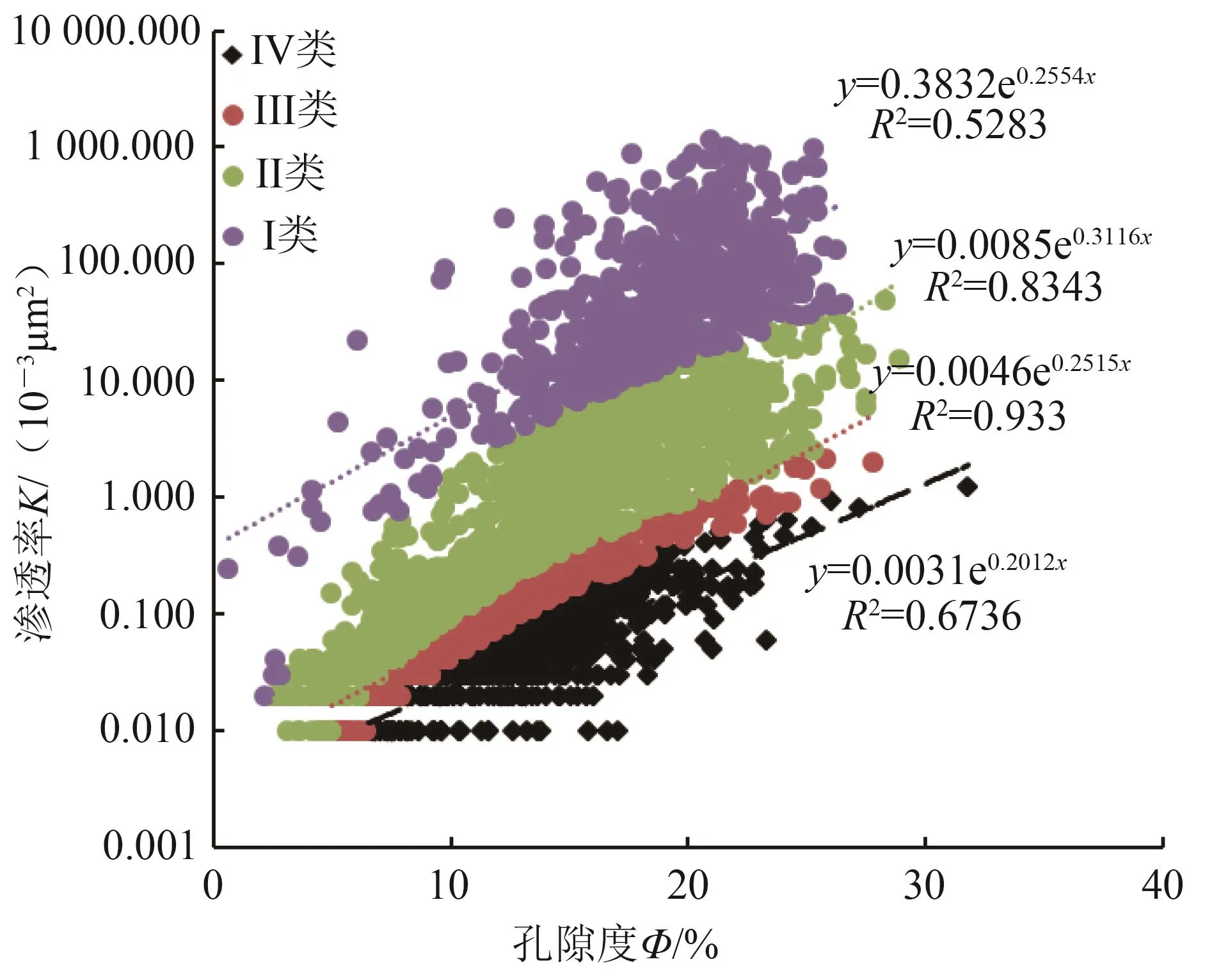
图5 分流动单元建立的渗透率模型Fig.5 Permeability model built by flow unit

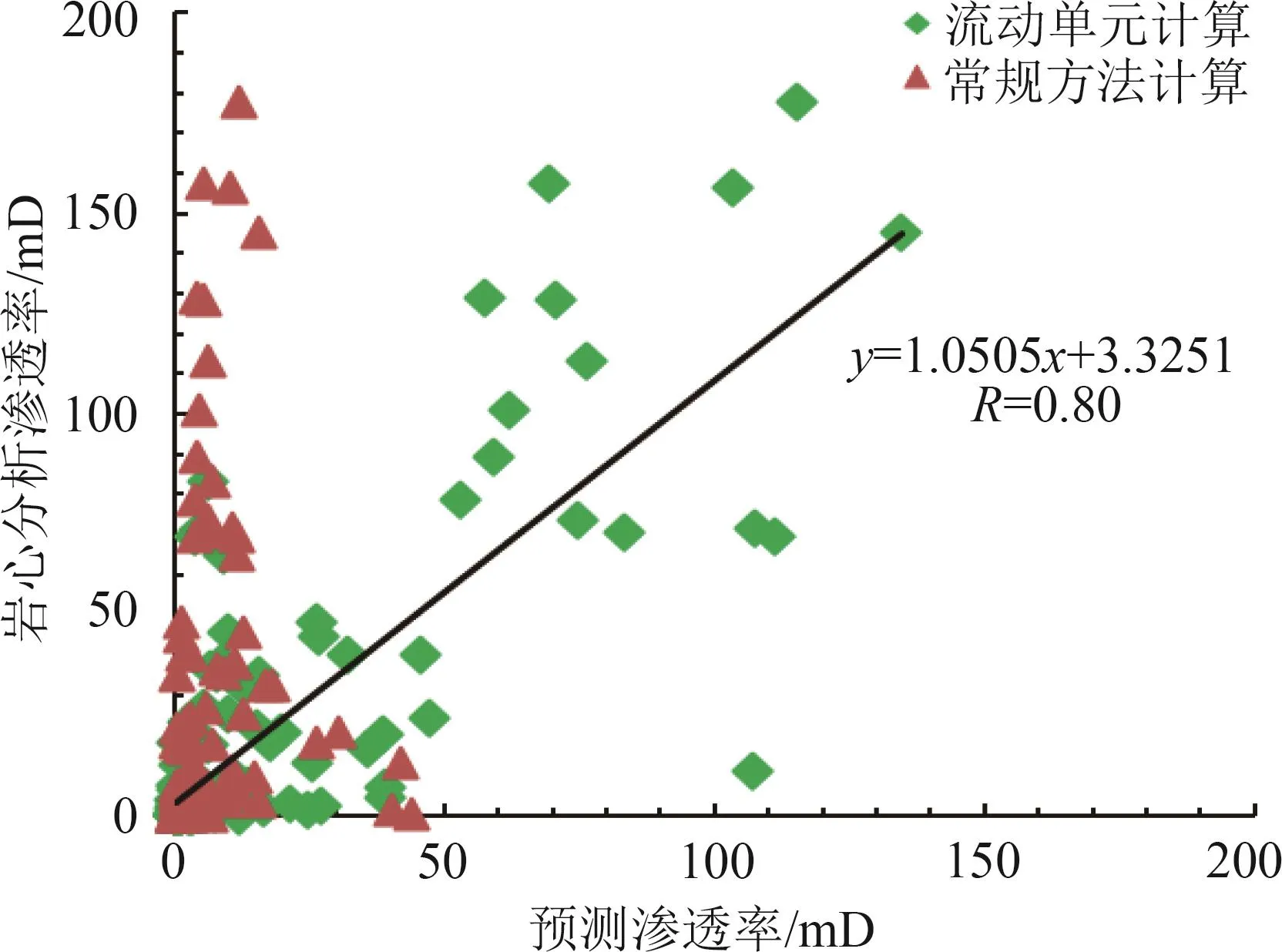
图6 分流动单元与常规计算结果误差对比图Fig.6 Error comparison diagram between flow unit and routine

5 结 论

5.1 凝灰质质量分数的增加导致渗透率呈下降趋势，同一孔隙度条件下，渗透率差异明显。

图7 塔02井FZI法计算渗透率与岩心分析渗透率对比图Fig.7 Comparison of permeability and core analysis by FZI method of tower 02 well

5.2 利用流动单元指数FZI将研究区划分为4类流动单元，随着FZI值的降低，棑驱压力值增大，孔吼半径变小，储集性能变差。

5.3 分流动单元分别建立了研究区的渗透率解释模型，渗透率解释精度明显提高。

5.4 应用判别分析法，建立取心段测井曲线参数

与流动单元划分之间的关系，并给出了各流动单元的Fisher线性判别方程。此方法可应用于其他非取心井的渗透率计算，具有较好的推广和应用价值。