空间句法在城市公园可达性研究中的应用——以武汉三环线内城市公园为例

张玉洋

孙雅婷

姚崇怀*

城市公园是城市居民在市、区范围内进行游憩娱乐、文化节庆和科普教育等活动的重要大型城市开敞空间；与其他公园相比，具有占地面积大，各项功能设施完备齐全，生态、社会及经济服务能力突出等优势[1]。因此城市公园在城市中的布局直接影响其到达性交通潜力和功能发挥程度[2]。通常，公园可达性指市民到达公园的相对难易程度，受距离、时间、费用及市民主观意愿等因素的影响。国外早期针对城市开敞空间可达性的研究方法多为问卷调查、范例研究和物理模型[3]，20世纪90年代开始加入GIS空间分析技术[4]。国内学者尝试运用网络分析、缓冲区法、引力模型、累积机会和距离分析等方法测算市民和城市公园之间的地理距离或空间阻力，量化公园可达性潜力[5]。

空间句法是20世纪80年代英国Bill Hillier教授团队创立的着眼于宏观连续空间客体构型关系与使用主体对空间片段感知叠加相互作用的城市空间结构形态分析的理论与技术[6]。其原理是分割空间并以分割后形成的子空间为图节点，将原有空间网络转化成节点连接图，借助图论法推导出系列分析变量描述空间组织规律并揭示其背后的社会文化内涵[7-8]。在城市规划和建筑学领域，空间句法的应用已十分普遍；丰硕的研究成果也对空间句法理论进行了补充和进一步完善。在风景园林领域，初期实践对象多为中小尺度空间，如中国古典园林内部场地[9]、古村落街巷空间[10]和居住区空间布局[11]等。随着GIS平台的兴起，研究范围上升至市域层面，包括城市防灾公园可达性[12]、滨水景观空间[13]和山地城市公园空间可达性[14]等，目前未涉及城市整体格局下的大型绿色开敞空间可达性评价。本研究借助空间句法，以武汉市三环线内城市公园为例，从公园在城市中的布局入手探究公园可达性程度，尝试为公园绿地评价提供一种新的技术方法。

1 研究方法

1.1 研究区域概况

武汉位于华中地区长江、汉江交汇处，被两江分为武昌、汉口和汉阳三镇，共7个主城区。截至2014年，共建成综合公园35个，总面积1701.32hm2，占城市公园绿地面积的25.7%。为避免边界效应，选择主城区内完整环闭城市快速路——三环线为研究边界，涵盖武昌范围内的洪山区、武昌区、青山区和部分 东湖高新区，汉阳范围内的汉阳区，以及汉口范围内的硚口区、江岸区和江汉区，以环线内29个城市公园作为研究对象。

1.2 可达性计量

1.2.1 空间分割模型

空间句法理论提出3种经典空间分割模型：凸状模型(convex map)、视域模型(visibility graph analysis)和轴线模型(segment map)。其中以轴线为模型单元的轴线模型契合城市道路特性适于城市尺度研究，尤其针对相对复杂的自由空间系统更为有效，例如欧洲百年小镇[15]。

武汉市属于相对简单的规整方格路网城市，本研究选择利用在轴线模型基础上优化后形成的线段模型，它将轴线单元于交点处打断成独立线段单元，以欧式距离限定研究半径，累计计算路径的角度转换。线段模型更贴近国内大尺度城市的空间导航和使用者寻路行为[16]，同时可直接利用城市GIS数据中的道路中心线构建模型单元，操作性和统一性更强。

1.2.2 模型变量值

城市公园句法可达性分析的实质是度测公园周边一定半径覆盖范围下的路网交通活力。线段模型中通常测度可达性的指标为平均深度(Mean Depth，)和整合度(Intergration，I)，其内涵及推导公式如下。

1)平均深度：为系统中某个节点到其他所有节点最短路程(即最少步数)的平均值，其数值越低，表示该节点更容易到达其他节点，网络的拓扑可达性高，反之拓扑可达性低。计算公式为：

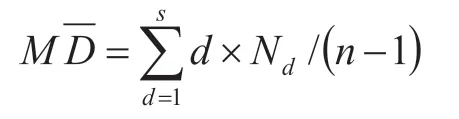
其中，d为节点最短角度路径，Nd为该深度上的路径个数，n为角度交叉点总数目。

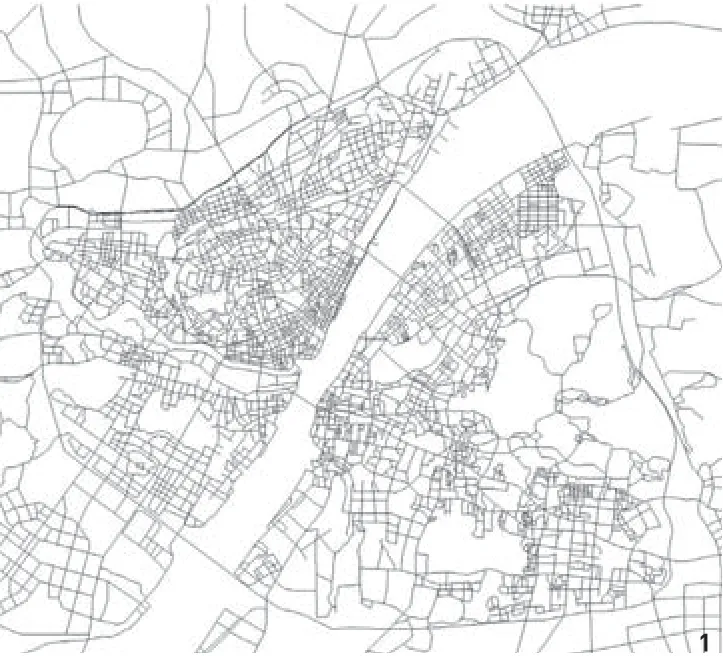
图1 武汉市城市干道线段模型

图2 武汉市三环线内城市公园面积及缓冲区截取

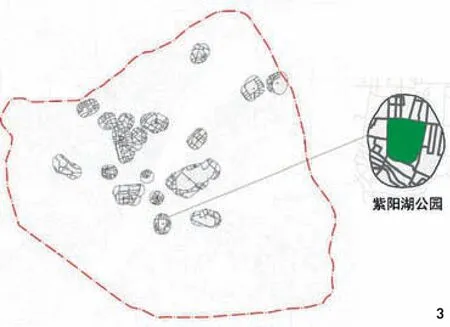
图3 公园缓冲面积线段模型及局部放大示意图

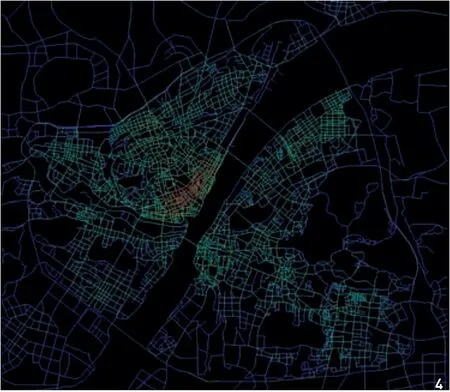
图4 半径2000m下的武汉市道路整合度分析(线段颜色越暖表示对应路段交通流量大、整合度高、可达性好)

2)整合度：表示一定半径下，某单元空间与系统中其他空间的离散程度。数值越大代表该空间在系统中到达性交通潜力越大；反之则潜力越小。为剔除节点数对整合度的干扰，空间句法引入了相对非对称性(Relative Asymmetry，RA)的概念：假设2种极端的网络，一种是所有节点都围绕目标节点连接，此时目标节点拓扑可达性最好；另一种是所有结点一字排开与目标点相连接，则目标节点的拓扑可达性最差。用平均深度值与这2种状态下的深度值做对比，得到一个相对值，称作相对非对称性。计算公式为：

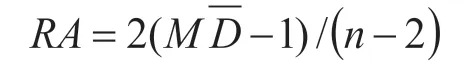
其中，n为节点总数，为平均深度。

然后，将得到的RA值与Dk值相比，得到实际相对非对称性RRA(Real Relative Asymmetry)，计算公式为：

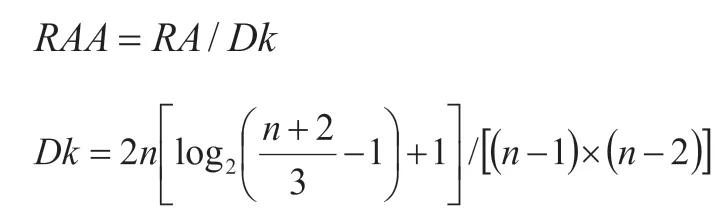
其中，Dk表示同数量节点排列成钻石型网络后最根部节点的RA值。

最后，为确保数据正向性，将取倒数，所得I值越大，可达性越好。计算公式为：

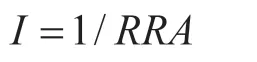
其中，I是一个相对值，受研究半径限制。

2 公园句法模型

2.1 市区线段模型

用2014年7月精度为多光谱30m×30m、全色谱15m×15m的landsat8武汉遥感影像结合Google影像辅以现场勘察校正，CAD绘制武汉市主要城市干道模型线段13159条，导入UCL大学开发的Depthmap10空间句法软件生成线段模型(图1)。

2.2 公园模型建立

在ENVI软件中对预处理后的武汉市遥感影像进行非监督分类和精准人工矫正，确保城市用地类型的准确性。再于GIS中矢量化截取三环线内的公园面积和服务半径500m内的缓冲面积(图2、3)。

2.3 R值确定

空间句法认为空间实测流量经标准化处理后与一定半径(R)下整合度呈现较强的相关性。选取18个具有客流量记载的公园和对应公园缓冲面积内线段模型(表1)，进行R值确定。

检验结果如表2所示，标准化处理后的公园实测客流量与半径2000m下的整合度为强相关性，Pearson相关性|r|=0.623，显著性(双侧)为0.006，下文研究将采用2000m作为默认半径选择。

3 武汉市综合公园可达性分析

3.1 公园选址的空间句法

从Deepmath中提取半径2000m下的武汉市道路整合度(图4)，从中再提取城市整合度前70%的路网与公园分布图相叠加(图5)，可知多数公园位于城市高可达性路网，地理位置优越；公园高密度点和高可达性路网的地理位置呈现出重合性。

公园密度最高点恰好在城市路网可达性水平最高的武汉市二环线的汉口(长江、汉江北岸)区域(图6)，包含解放公园、中山公园2个全市性公园，以及后襄河公园、菱角湖公园、西北湖公园、喷泉公园、宝岛公园和小南湖公园6个区域性公园。这种“局部加密”现象表明：可达性高的区域交通流量高，人流会对公园造成一定使用压力，增加公园数量不仅能缓解人流压力，也可为该区域的市民提供更多出行选择。

表2 不同半径的句法参数与公园实测流量的相关性分析结果

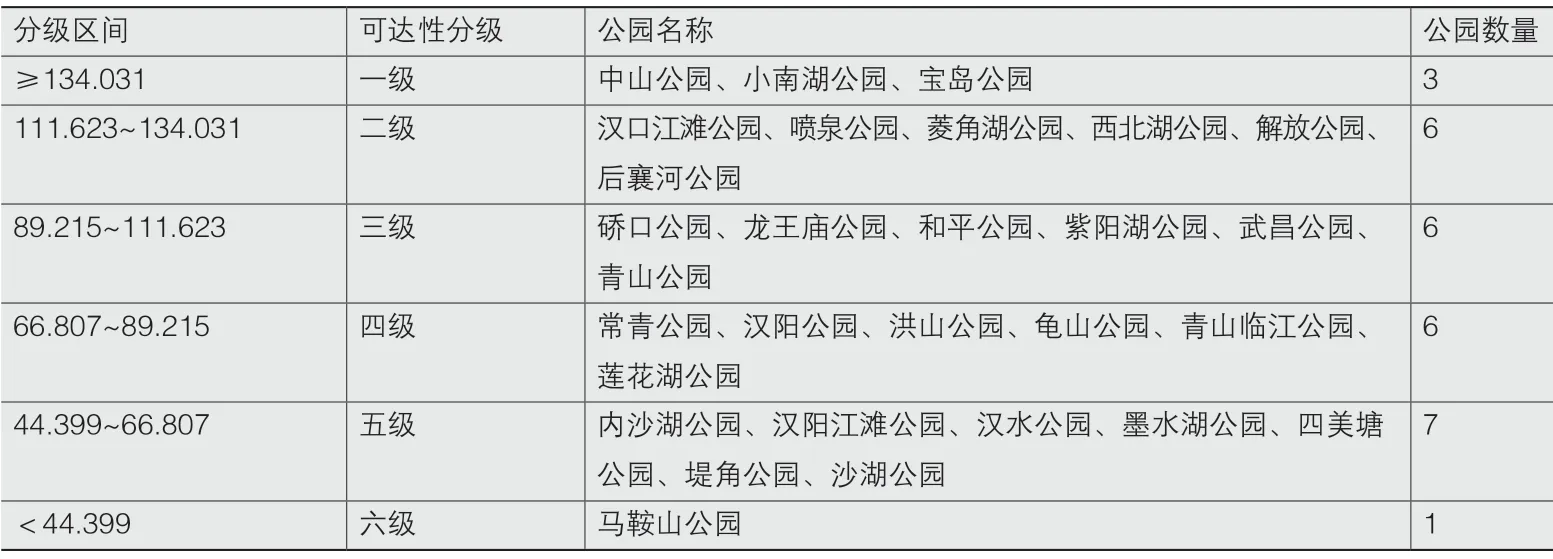
表3 武汉市综合公园句法可达性分级汇总

另外，在西部长丰片区、北部的后湖片区以及西南角光谷片区等活力次中心无城市公园辐射。长丰片区和后湖片区属于居住用地，市民以社区公园需求为主；光谷片区是以商业科研为主的综合用地，人流量大、人群类型丰富，但与其距离最近的马鞍山森林公园无高可达性网络连通，不易到达。

3.2 公园可达性的空间句法

提取公园缓冲面积内道路的句法模型图(图7)并根据整合度数值划分出6个等级(表3)，得到高可达性公园8个，其中一级公园(Int≥134.031)3个、二级公园(111.623＞Int＞134.031)5个；中可达性公园(89.215＞Int＞66.807)13个；低可达性公园(Int＜44.399)1个。可见城市公园可达性等级结构呈现不均衡状态。

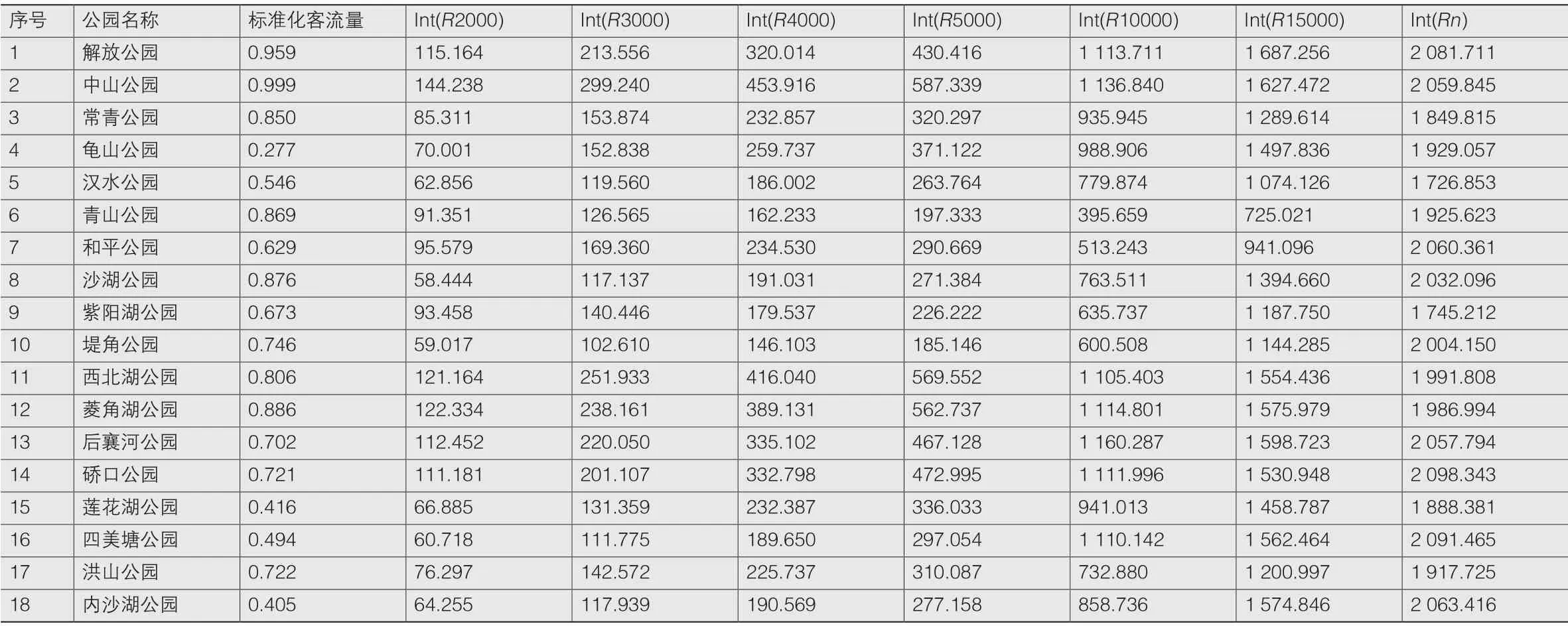
表1 公园句法模型参数值汇总

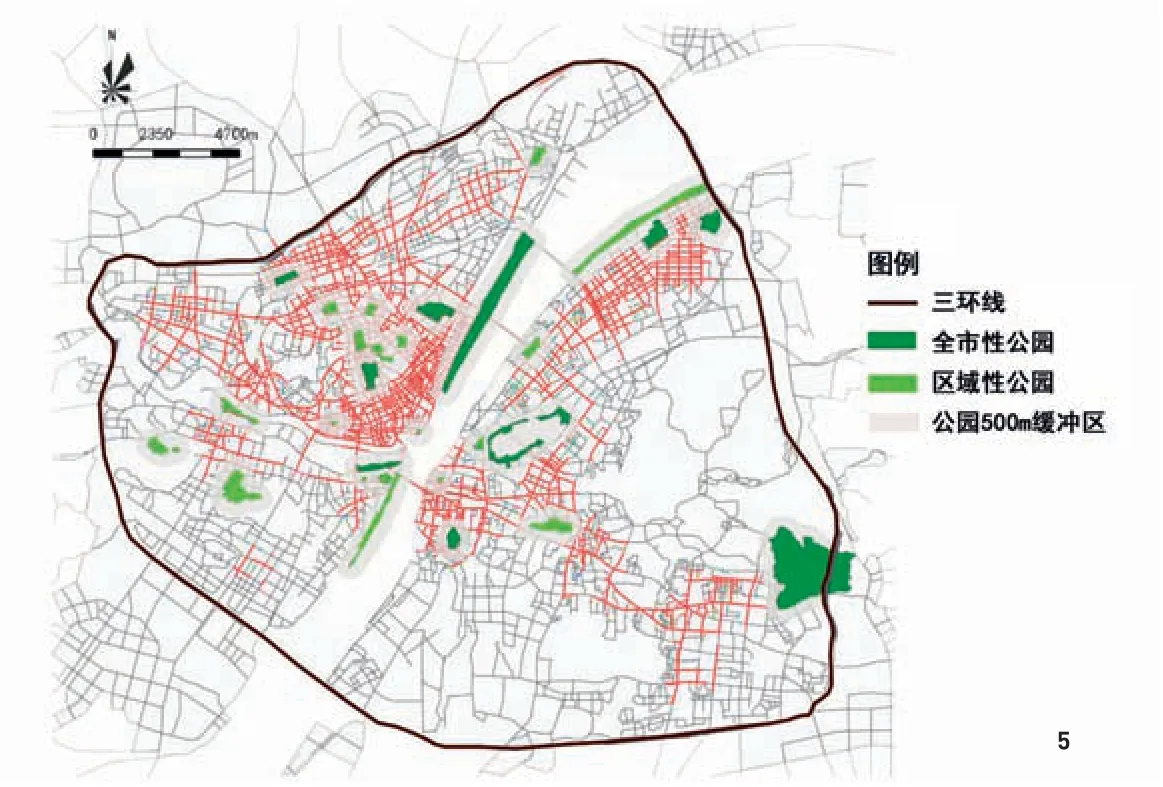
图5 武汉市三环线内城市公园区位分析

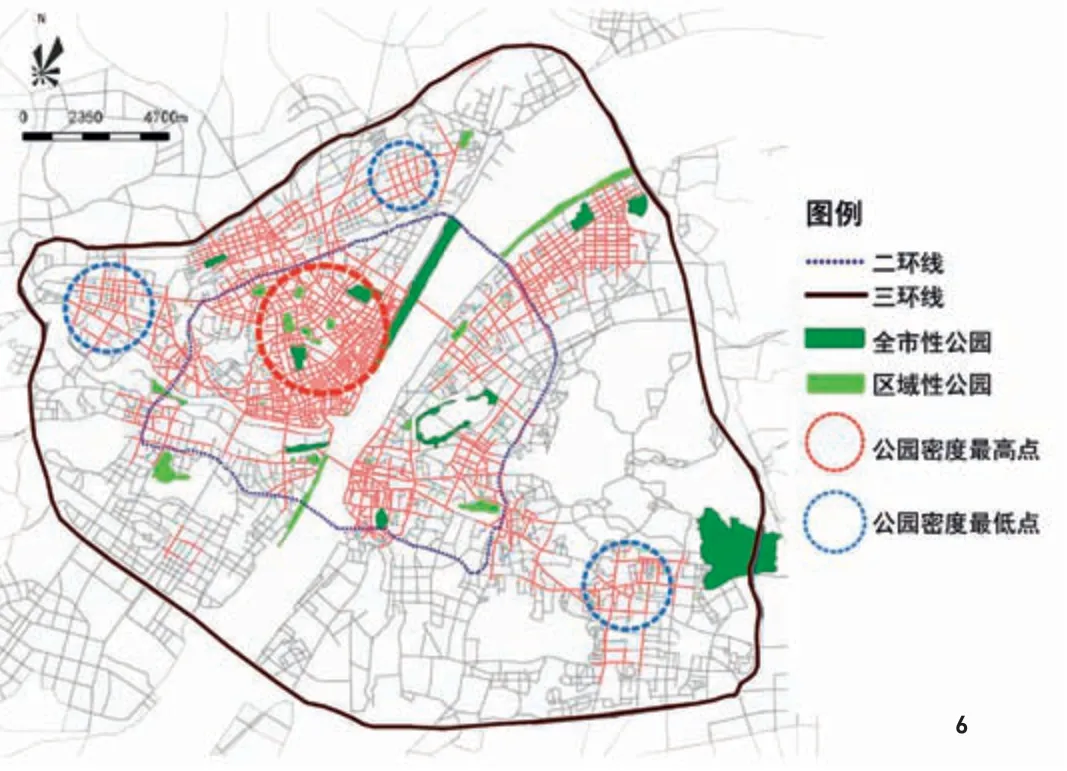
图6 武汉市三环线内城市公园密度分析

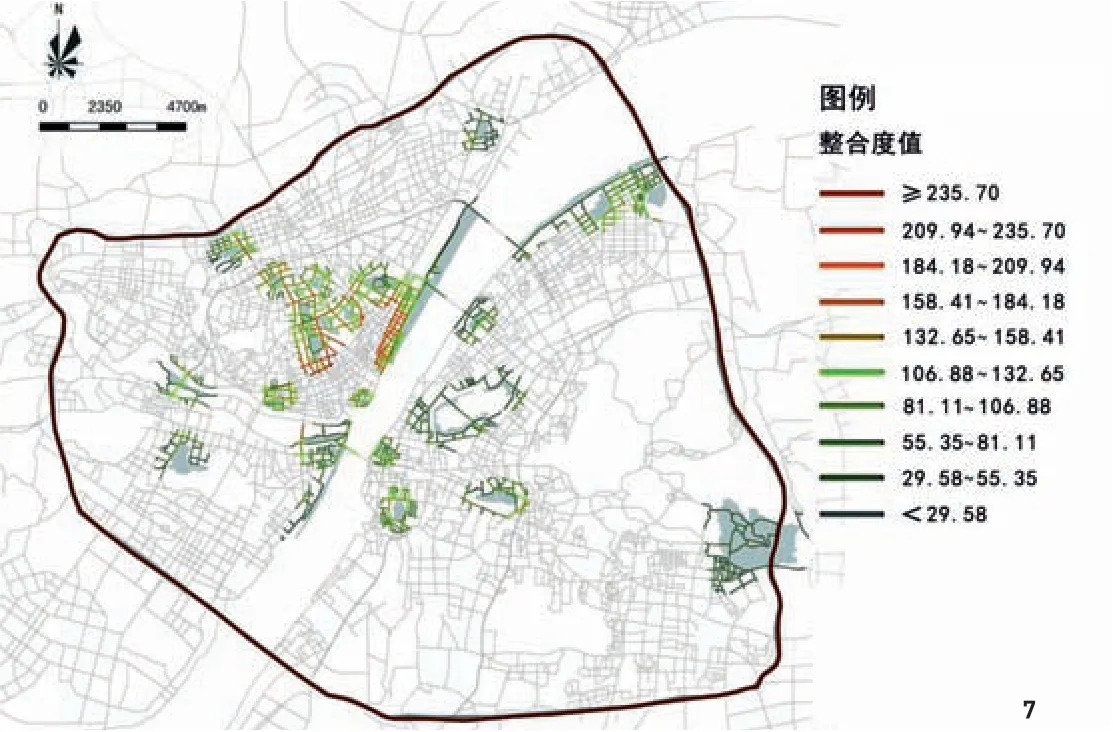
图7 武汉市三环线内城市公园缓冲面积内道路句法模型

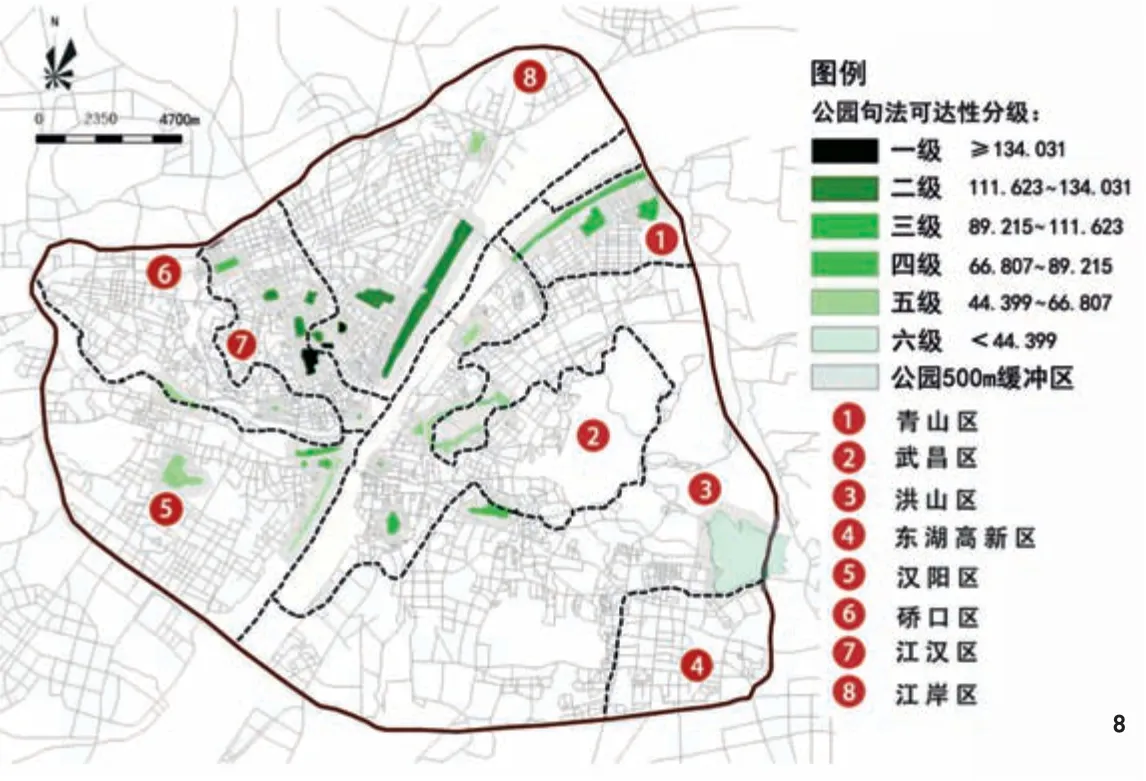
图8 武汉市三环线内城市公园可达性等级分布

不同可达性等级公园并非均质分布于城市之中(图8)，高可达性公园都集中分布在江岸、江汉两区交汇处和江岸区沿长江一带；中可达性公园散布于其他各区；可达性等级最低的马鞍山公园位于洪山区的西南角，位置较为偏僻。

3.3 基于人口密度叠加的公园可达性评估

将公园可达性分级图和城市人口密度等级图[17]在GIS中叠加(图9)发现，武汉市人口密度呈由中心向外围递减的趋势，与综合性公园可达性分布情况总体吻合。高可达性公园多分布在高密度人口区域，如江岸、江汉交界及沿江地段、青山区中心部分，同时这些区域内的公园四周与整合度较高的道路连接，可有效引导附近居民快捷抵达。汉阳王家湾片区的汉水公园、墨水湖公园可达性均较低；汉口江岸的百步亭片区仅有汉口江滩公园；武昌洪山区、武昌区有大片次高等级(300～500人/km2)的人口密度分布区，但仅有一个等级较高的小南湖公园，明显不能满足居民使用需求。

将公园入口分布情况与公园周边道路整合度相叠加(图10)，可知少数公园入口位置未与公园周边整合度高的道路相结合，其中以解放公园和洪山公园最为明显(图11)。

解放公园入口设置未与公园西侧整合度较高(132.65～158.40)的惠济路结合，因此可增设入口利于紧邻的高人口密度(500～800人/km2)的竹叶山片区市民便捷到达；洪山公园入口方位单一且地理位置偏僻，不利于便捷到达，可适当在公园北面及东北面增设入口方便市民使用。

4 结语

通过空间句法可达性分析发现武汉市三环线内城市公园呈聚集性分布，与武汉市人口密度分布保持一致，总体空间布局合理，在后期公园建设中可持续保持这一原则。

同时，城市公园的分布也表现出区域间的不平衡，85%的高可达性公园主要集中在汉口地区；武昌、汉阳地区的公园整体可达性相对较弱，总体公园可达性等级分布结构失衡。这种资源分配的不均会影响城市居民享受公共服务设施的公平性。在城市未来的规划建设中，可通过在武昌、汉阳等地增建公园数量或优化公园周边路网来消除低整合度盲点，提升公园可达性。

本文作为试验性研究发现空间句法在国内方格路网型城市中的实践性良好，但是针对目前城镇化快速发展的情况，仍存在如下欠缺与不足。

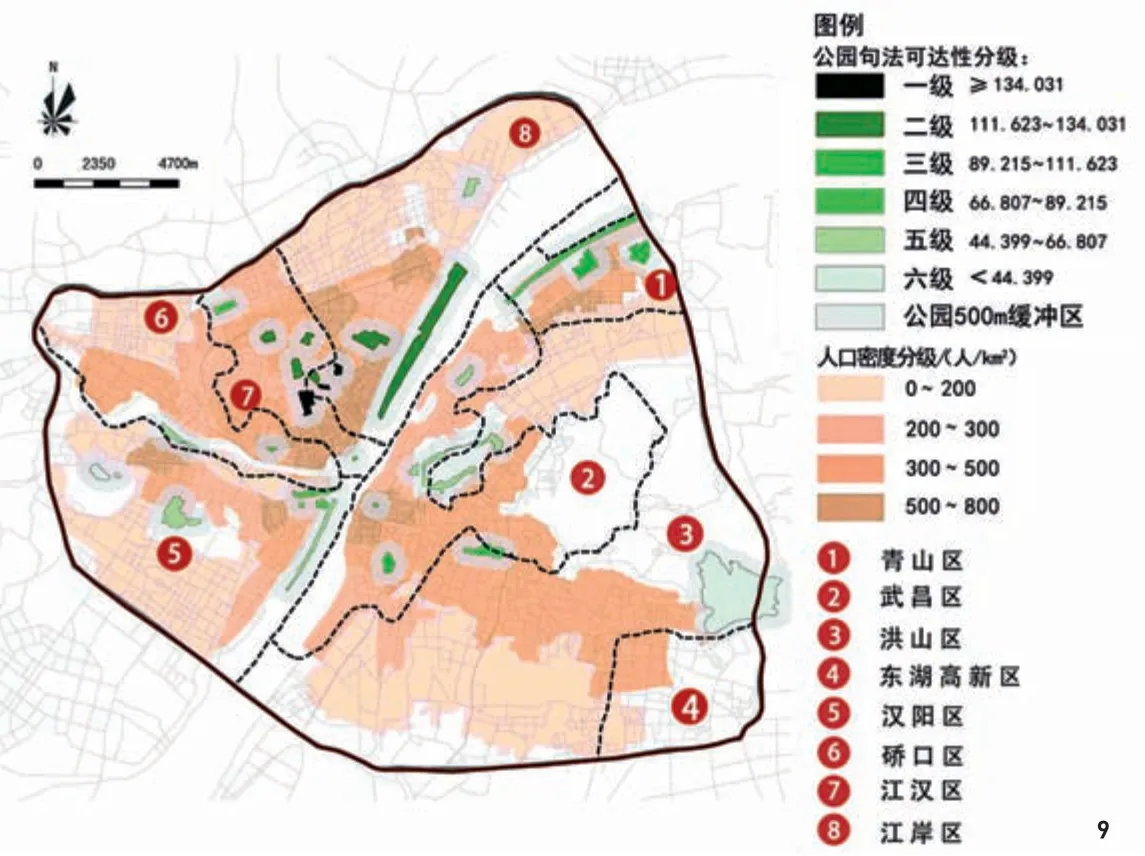
图9 公园可达性等级与城市人口密度等级叠加分析

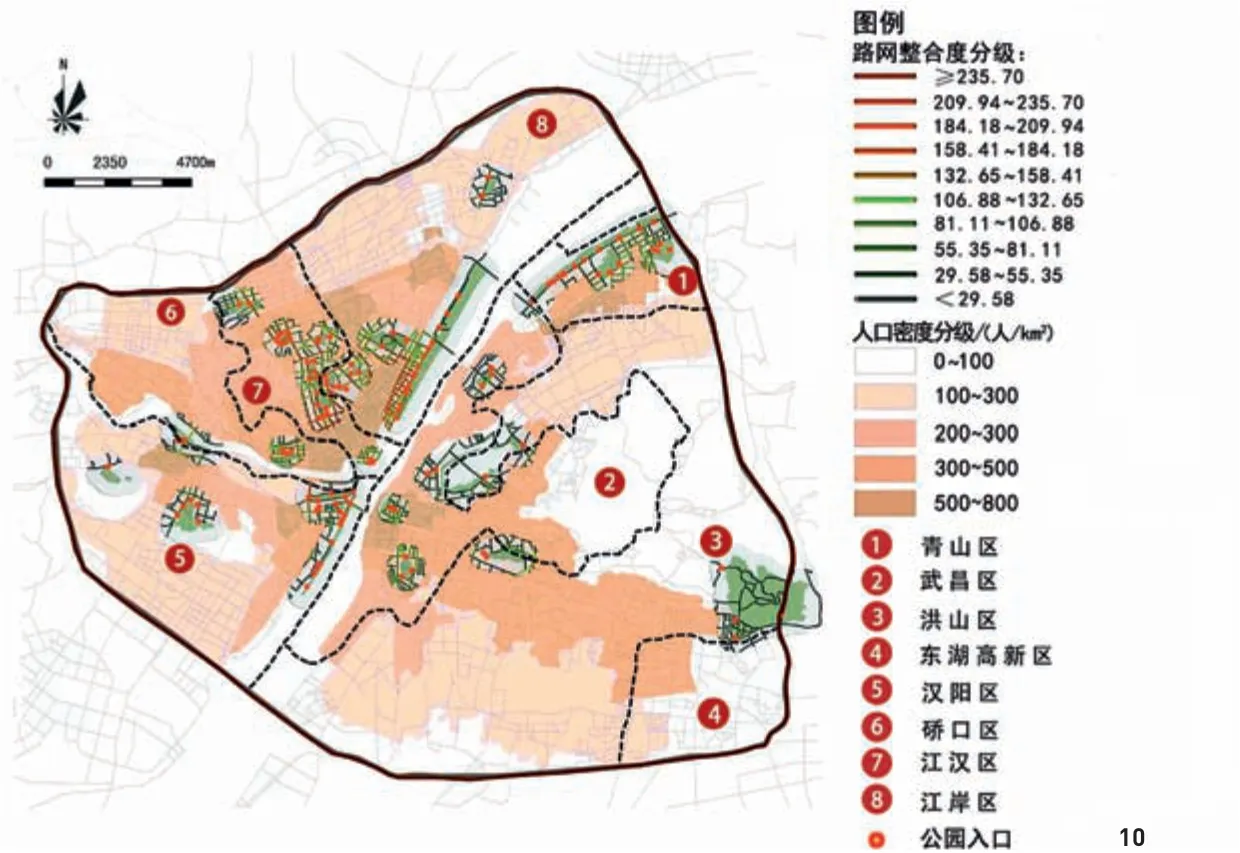
图10 公园入口分布与城市人口密度等级叠加分析

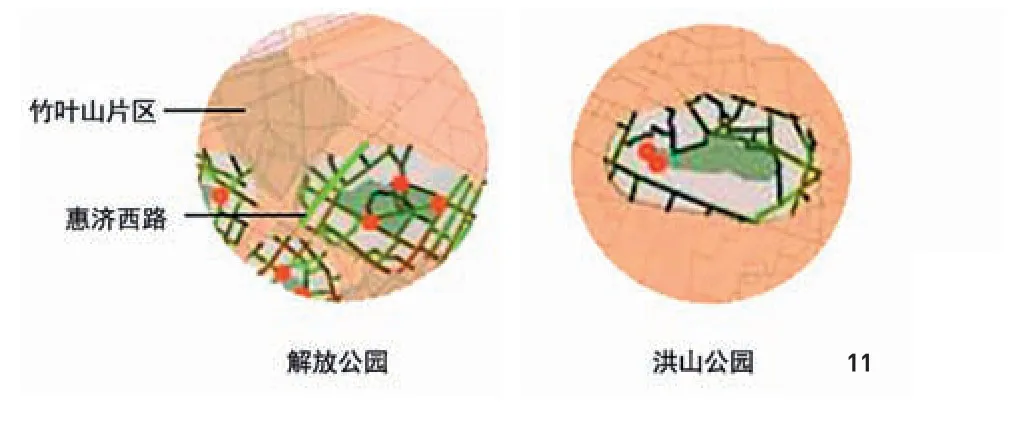
图11 解放公园和洪山公园放大图

1)绘制武汉城市干道线段模型图时，尽可能确保模型的精确与完整。但局部地区数据获取困难，少数模型线段的识别误差依然存在。今后结合城市大数据开展类似研究应能获得一个较好的解决方案。

2)现代城市交通系统已形成较成熟的空中、地面、地下三维交通方式，在现阶段模型表达中未找到相对妥善的解决方案；目前诸多学者正尝试新模型，有望在未来出现更准确的城市模型表达。

3)除绿地外，城市中还有交通、商业等其他大型开敞空间，如何将绿色空间可达性和其他工作、生活空间的可达性相叠加进行关联和整体分析，将对城市规划建设和各类开敞空间布局提供新的视角，为城市规划建设提供更加科学的建议和理性设计基础。