地磁场水平分量的测量
陈易楠
(浙江省萧山中学 浙江 杭州 311201)
2019年5月我校举行了第二届青年物理学家锦标赛,其中一个问题是:地磁场的存在保护了人类的安全,请你设计实验测定当地的地磁场的磁感应强度大小和方向.
我们小组使用两种方法测量了地磁场.
1 反转法
1.1 原理介绍
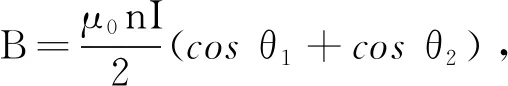
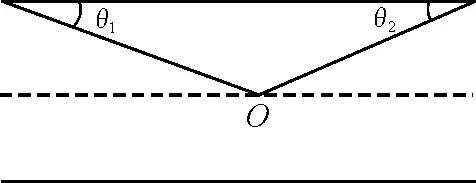
图1 原理图
螺线管反转法是将一南北指向的小磁针平行置于一螺线管轴线位置,通过逐渐增大螺线管中的电流,直至螺线管在轴线处产生的与地磁场反向的磁场恰好令小磁针发生反转,则认为此时螺线管在磁针处产生的磁感应强度近似等于地磁场的水平分量[1].
螺线管反转法虽然相对巧妙地通过磁针的反转近似测得了地磁场水平分量的大小,但由于磁针本身阻力矩的存在,以及所取电流值为磁针已经发生反转时的电流值,最终测得的地磁场不可避免地会大于真值,并且将磁针置于螺线管内进行实验,对实验的观察也带来了较大的不便.
1.2 改进
针对磁针观察不便的问题,我们将磁场发生装置删繁就简,退化为一用N匝线圈在同一圆环上环绕产生的导线环,设电流为I,圆环半径为a,由毕奥-萨伐尔定律可知环形电流在距中心轴线r处的磁场大小B(r)为[2]
再利用与之前类似的反转法对地磁场大小进行测量.
针对磁针本身阻力矩的影响以及反转磁场大于地磁场的系统误差,我们通过正反补偿来进行一定的修正,即通过增大电流直至磁针反转时,测得第一组电流大小I1,再减小电流至磁针再次反转恢复原指向时测得第二组电流I2,取
代入上述B(r)的公式计算得到的磁场即认为是补偿之后相对精确的地磁场大小.为呈现补偿法的效果,我们进行了有无使用补偿法的两组实验并进行结果的比较.
1.3 实验步骤和仪器介绍
(1)在塑料圆环上紧密缠绕了7匝的线圈并将进出圆环的两根导线并成一根以排除其电流磁效应的影响.
(2)用直尺测量圆环的半径a.
(3)如图2所示连接电路.
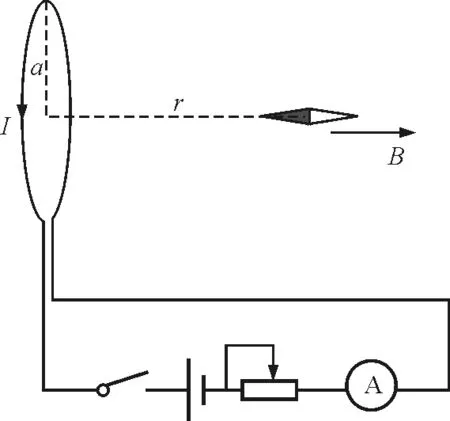
图2 实验连接电路
(4)固定导线环并将磁针平行置于其轴线上,使磁针所指方向与导线环所在平面垂直,记录磁针中心到导线环面的距离r.
(5)接通电源,调节滑动变阻器缓慢增大直至磁针恰好反转记录电流表的示数I1,再逐渐减小电流直至小磁针恢复原指向,记录此时电流表的示数I2.
(6)改变r的值,进行多次测量,记录多组I1,I2的值.
(7)数据处理,并计算不确定度.
(8)利用相同装置在不使用补偿法的前提下重复上述实验,计算结果进行对比.
本实验采用的环形电流共有N=7匝,半径a=3 cm.
1.4 实验结果
未使用补偿改进的反转法实验结果如表1所示.使用补偿改进的反转法实验结果如表2所示.
表1未使用补偿改进的反转法实验结果
N=7匝 半径a=3 cm
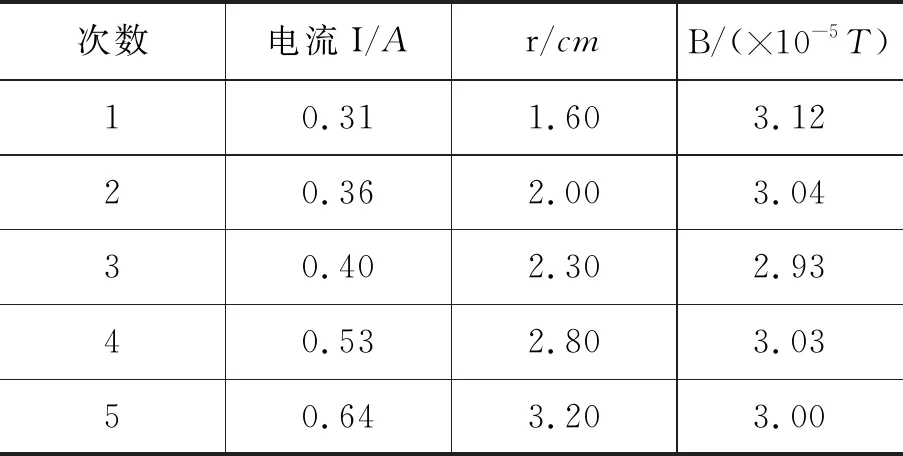
次数电流I/Ar/cmB/(×10-5T)10.311.603.1220.362.003.0430.402.302.9340.532.803.0350.643.203.00
可得
B=(3.02±0.03)×10-5T
其不确定度由公式[4]
给出.
表2使用补偿改进的反转法实验结果
N=7匝 半径a=3 cm
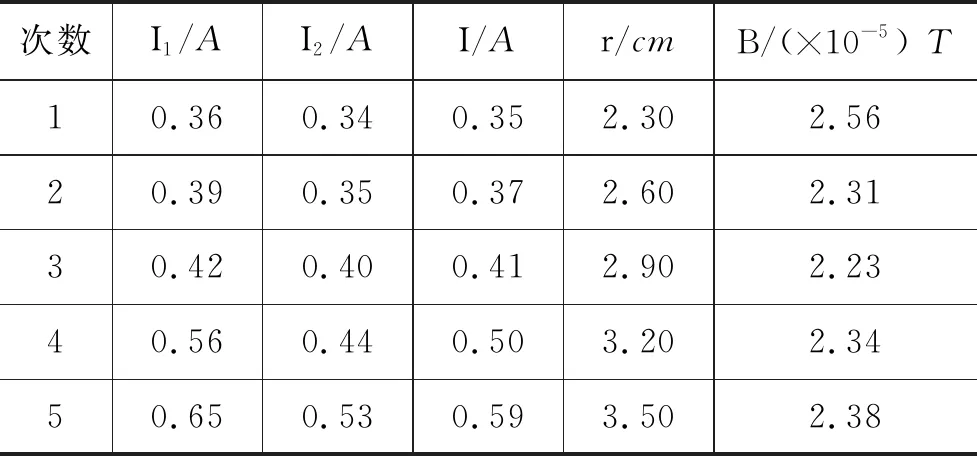
次数I1/AI2/AI/Ar/cmB/(×10-5) T10.360.340.352.302.5620.390.350.372.602.3130.420.400.412.902.2340.560.440.503.202.3450.650.530.593.502.38
可得
B=(2.37±0.07)×10-5T
可以看到使用补偿法后测得的磁场的磁感应强度大小明显小于未使用补偿法时测得的磁感应强度大小,说明补偿法较好地排除了阻力矩以及反转产生的系统误差.
1.5 再改进
自始至终,我们利用磁场发生装置产生平行于地磁场方向的磁场进行实验,但难免存在以下误差:
①如何保证小磁针与地磁场严格平行;
②电流产生的磁场并不均匀;
③磁针有一定的尺度,它的中心难以确定.
因此我们考虑改进实验,利用通电直导线产生垂直于地磁场方向的磁场,二者的叠加场令小磁针进行偏转.
2 直线电流叠加法
2.1 原理简析
无限长通电直导线I在r处产生的磁感应强度大小为[3]
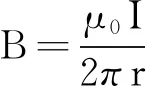
(1)
如图3所示,将通电直导线平行于地磁场方向放置,并在其下方放置一小磁针,便可由小磁针的偏转角θ得到通电直导线产生的磁场与地磁场磁感应强度的比值,即
(2)
由式(1)、(2)可得
(3)
即r与cotθ成线性关系,所以,只要测得一系列r与θ的值,便可得出地磁场的大小.

图3 直线电流叠加法实验装置图
本实验采用最小二乘法进行数据处理,即对所得的数据点进行直线拟合[5],所得斜率为
变形得
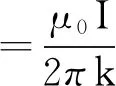
(4)
值得注意的是,由于采用了最小二乘法,所以所测距离r并不必须为磁针中心与直导线的距离,只要使r的零点相同,所得直线只是将标准直线进行上下平移,对斜率并无影响.
2.2 实验过程及结果展示
按如图4所示连接电路,断开开关,使长直导线与小磁针初始指向平行.
调整导线与小磁针距离,记录数据r,闭合开关,记录电流I和小磁针偏转角度θ,改变导线与小磁针距离r,用滑动变阻器保持电流不变,记录多组r与θ的数据,对所得结果进行数据处理,分析得到结论.
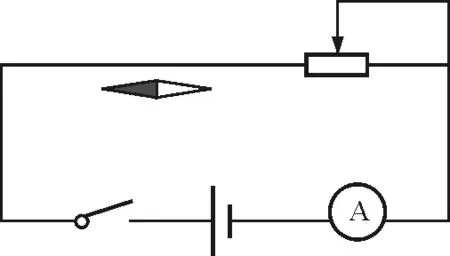
图4 直线电流叠加法电路图
本次实验中,电流保持I=0.7 A不变.
实验结果如表3所示.
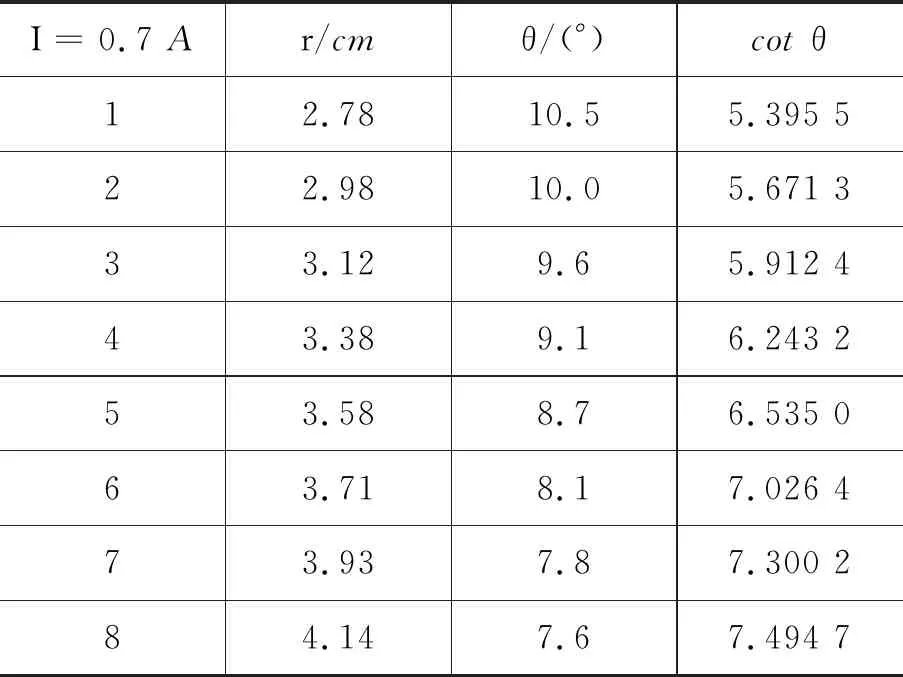
表3 直线电流叠加法实验结果
利用最小二乘法做出拟合直线如图5所示.
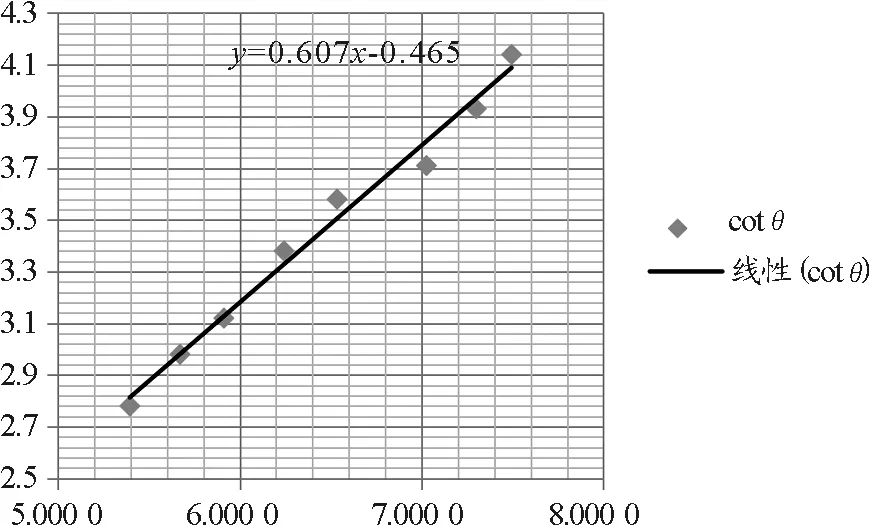
图5 最小二乘法拟合直线
将I=0.7 A,k=0.607 6代入式(4)可得
B=2.31×10-5T
2.3 误差分析
(1)小磁针转动存在阻力,所指向不是精确的合场强方向.
(2)各类仪器本身的系统误差和读数时的偶然误差的影响,电流尽管有调整但无法保证每次数值都完全相同.
(3)磁针偏转角由量角器测出,读数有误差.
(4)外界电路,金属等物品对所测磁场有干扰.
3 小结说明
(1)两次实验的结果
B=(2.37±0.07)×10-5T
和
B=2.31×10-5T
非常接近,并与真值符合得很好.
(2)实验二所用导线不可能为无限长,对此产生的系统误差进行如下说明.
有限长直导线在r处的磁场大小为
本实验中,测得导线长度l=1.63 m,假定距离r=0.1 m(已经大于本实验中的最大距离取值),取θ1=θ2计算得
完全可以忽略不计,故用无限长通电直导线的磁感应强度公式不会造成太大的误差.

