侧风状态下剪刀型尾桨的气动噪声特性

代 军 何 强 汤 艳 张 伟

（西南科技大学土木工程与建筑学院 四川绵阳 621010）

直升机作为一种能够垂直起降、悬停、小速度飞行的飞行器，在民用和军用等领域都有广泛应用，但直升机噪声较大的特点制约了其进一步应用。直升机的旋翼和尾桨通常是直升机气动噪声的主要来源。在特定的飞行状态下，直升机尾桨噪声会急剧增大，导致尾桨噪声成为直升机总噪声的主要来源［1］。

随着计算机技术与数值计算方法的发展，计算流体力学（CFD）方法逐渐成为直升机噪声研究的重要手段。对直升机旋翼和尾桨噪声的研究分为尾桨流场的计算与气动噪声的计算。

旋翼数值计算方法的发展可以分为4个主要发展阶段，每个阶段所使用的方程分别是：小扰动方程、全位势方程、Euler（欧拉）方程以及Navier-Stokes（N－S）方程。20世纪80年代中期，Roberts等［2］建立了一套适用于旋翼悬停流场的计算方法，该方法首次将欧拉方程运用到旋翼流场的求解中。西北工业大学的学者王立群等［3］用网格中心有限体积法对具有两片桨叶的旋翼在亚声速与跨声速运动下的压强分布进行了计算。童自力等［4］采用带有动量源项的N－S方程，对不同构型的直升机旋翼的流场进行了模拟，并分别研究不同构型旋翼的气动力特性。南京航空航天大学［5－6］、中国直升机设计研究所［7］等采用CFD方法对直升机尾桨气动流场进行了研究。

目前，研究旋翼气动噪声的数值模拟方法中大多数都使用到了FW－H方程与Kirchhoff方程。20世纪60年代后期，英国的Williams等［8］提出了著名的FW－H方程，可以用于精确计算任意固体边界与流体相互作用而产生的噪声。20世纪80年代，Farassat［9］基于FW－H方程，经过一系列的推导，最终得到了Farassat 1公式，并在其基础之上又导出了Farassat 1A公式。西北工业大学的韩忠华等［10］运用欧拉方程与FW－H方程对直升机旋翼悬停状态与前飞状态的声场做了计算，并取得了较为理想的结果。王立群等［11］进行了直升机旋翼桨尖形状对噪声量级影响的研究。

剪刀型尾桨是一种常应用于武装直升机的尾桨构型，其由上下两对非等距、有间距排列的桨叶构成。由于其桨叶分布是不等距的，临近的两片桨叶在某些交叠角下间距会很小，导致两片桨叶之间会有强烈的气动干扰。已有研究表明，非等距角桨叶布置引起的“调制效应”使得剪刀型尾桨具有一定的降噪能力［1］。目前已有的研究主要是针对其悬停和前飞状态的噪声特性［12］。在侧风状态下，尾桨易进入涡环状态导致尾桨气动失效，而剪刀型尾桨特殊的几何构型，使得其进入涡环状态的运动行为更复杂，剪刀型尾桨流场的复杂性同时也导致了其气动力和气动噪声特性的复杂性。据作者调研，目前尚未有针对剪刀式尾桨在侧风状态下的气动力和气动噪声特性的系统研究。

基于此，本文运用计算流体力学的方法首先对直升机尾桨的流场进行计算模拟，得到必要的流场数据，再将尾桨流场数据输入到噪声计算模型中，对尾桨的气动噪声进行研究，分析侧风状态下剪刀型尾桨的几何构型（轴向间距及交叠角）对尾桨气动力和气动噪声特性的影响。

1 计算模型及方法

1.1 剪刀型尾桨模型

本文针对Lynx旋翼［13］来研究L型剪刀型尾桨的气动力特性，其尺寸参数为：桨叶翼型采用NPL－9615，旋转半径（R）为1.105 m，弦长为0.180 m，无负扭转，桨叶数为4。L型尾桨如图1所示，其旋转在前的桨叶低于旋转在后的桨叶。

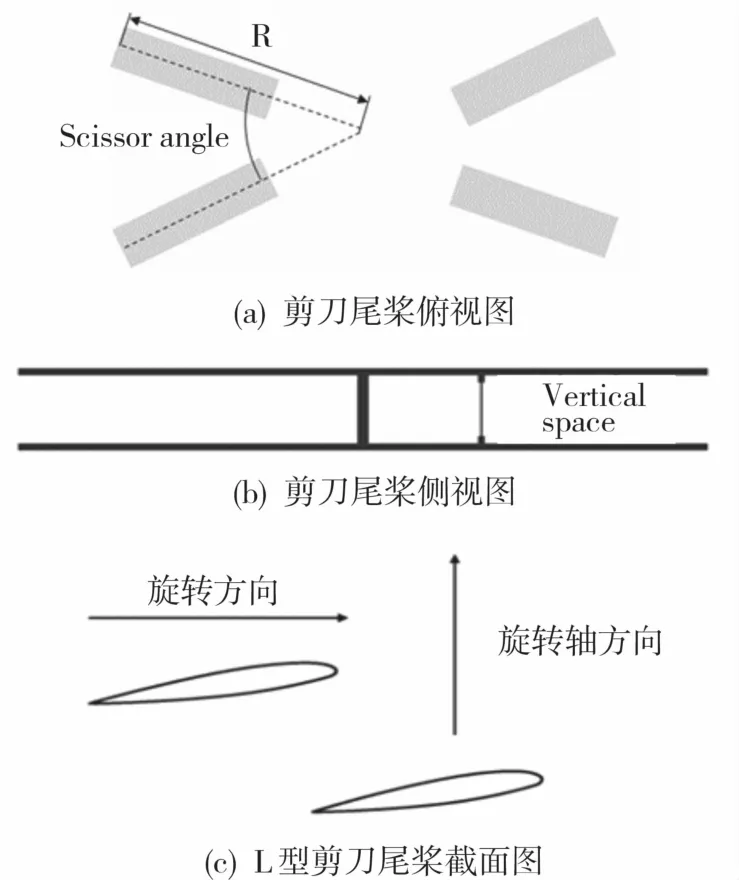
图1 L型尾桨示意图Fig.1 Schematic diagram of the L－shaped tail rotor

1.2 计算域

整个流域分为内部计算域与外部计算域，内域为直径3 m、高0.3 m的圆柱状流域，如图2所示。外域为高100 m、底面边长为150 m的方形区域，内域在距离进口30 m截面中心处，如图3所示。

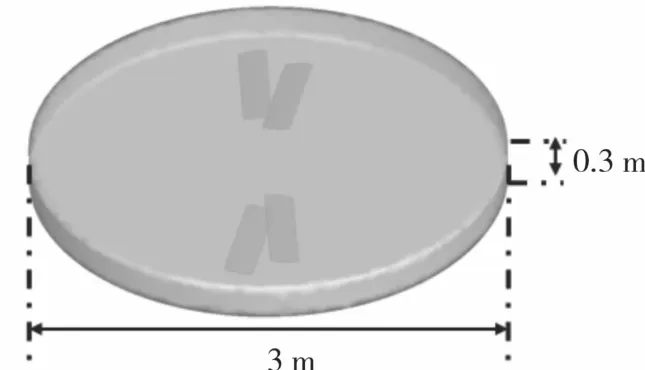
图2 内流域示意图Fig.2 Schematic diagram of the internal domain

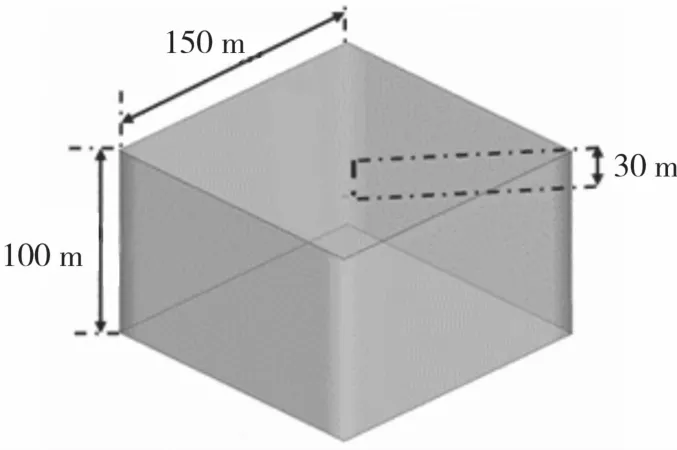
图3 外流域示意图Fig.3 Schematic diagram of the external domain

1.3 网格划分及边界设置

由于剪刀型尾桨结构较复杂，故采用混合网格进行网格划分，即将整个计算域划分为内部和外部两个部分。内部小区域划分为小尺寸的非结构网格，桨叶表面网格加密并添加边界层网格（图4）；外部区域采用结构网格（图5及图6）。经过网格收敛性验证后，确定各算例总的网格数大约在700万左右。

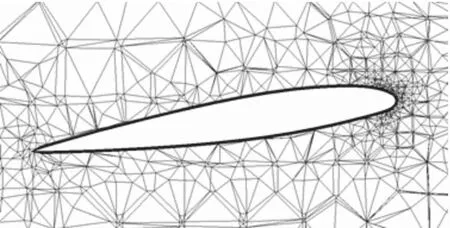
图4 桨叶网格截面Fig.4 Grids around airfoil

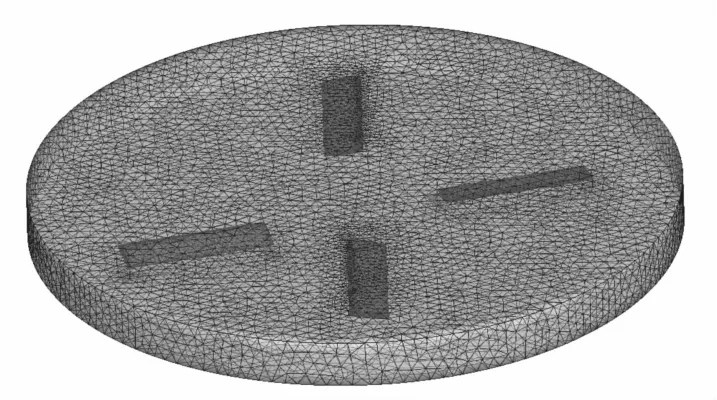
图5 内部流域非结构网格Fig.5 Unstructured grids ofinternal domain

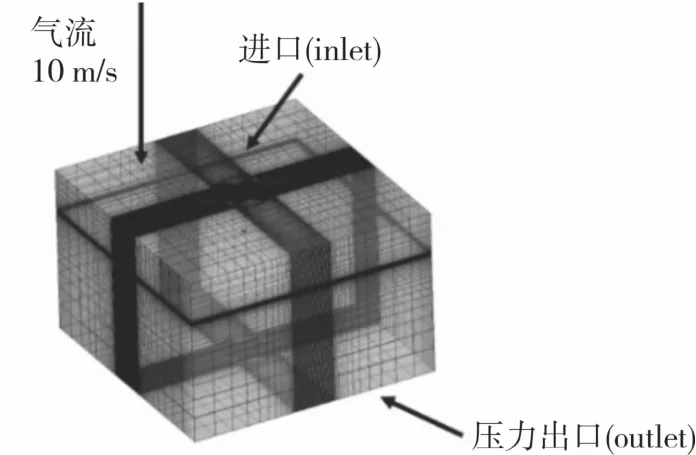
图6 外部流域结构网格及边界条件Fig.6 Structured grids of external domainand boundary conditions

1.4 求解器设置

本次计算模拟采用密度基求解器，三维非定常计算。计算时选用k－ε湍流模型，内部计算域为旋转区域，其角速度为184.6 rad／s，即桨尖马赫数约为0.6，侧风状态时垂直于尾桨盘面的来流速度为10 m／s。采用滑移网格实现尾桨的旋转运动，尾桨所在圆柱区域为内部运动区域，外部为静止区域，内外计算域之间设置一对交界面，通过插值来实现动静区域的数据传递。噪声计算选用Ffowcs-Williams＆Hawkings噪声模型，采用隐式的一阶迎风格式，时间步长设置为0.000 472 66 s。

2 剪刀型尾桨气动力特性

剪刀型尾桨有比常规尾桨更为复杂的结构，其气动力特性会受到其构型的影响。交叠角与轴向间距都是影响因素，研究清楚剪刀型尾桨的交叠角与轴向间距对其气动特性的具体影响对剪刀型尾桨的参数设计是非常重要的。

拉力为垂直于旋转平面的向上的合力，此处采用无量纲化的拉力系数来描述，其定义为：

其中，T为尾桨拉力，ρ为来流密度，U为来流速度，S为桨叶的横向截面积。

为了更好地研究相同间距下交叠角对剪刀型尾桨气动力特性的影响，通过固定间距变化交叠角的方式进行计算。交叠角在0°～90°之间，每隔15°计算一个工况。图7和图8给出了轴向间距为0.1R和0.08R时的各交叠角的拉力系数随时间变化图，从图中可以看出，拉力系数随着迭代进行逐渐收敛达到稳定值。

图7 尾桨间距为0.1R的各交叠角的气动力监测图Fig.7 Aerodynamic monitoring diagram of each overlapping angle at a vertical space of 0.1R

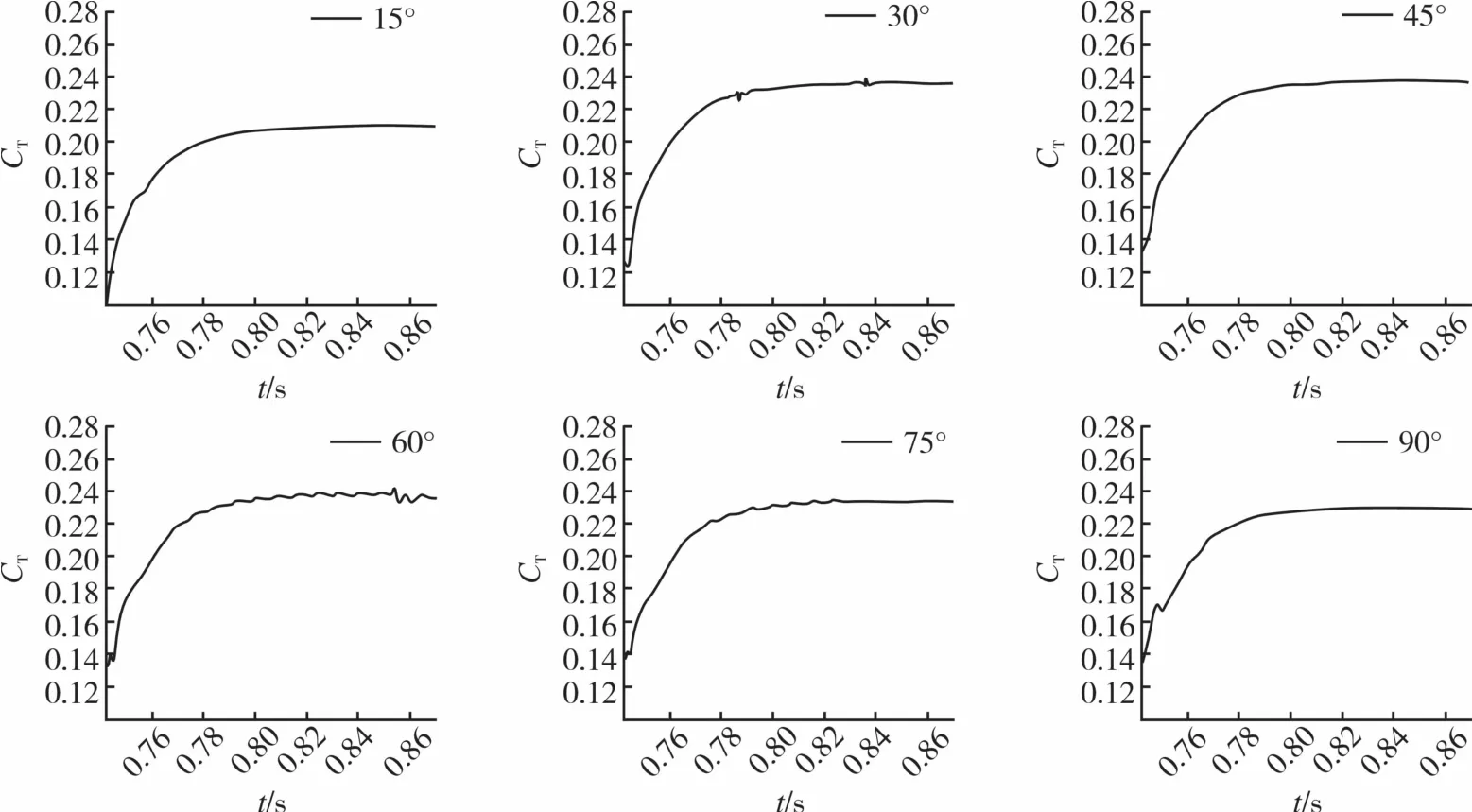
图8 尾桨间距为0.08R的各交叠角的气动力监测图Fig.8 Aerodynamic monitoring diagram of each overlapping angle at a vertical space of 0.08R

图9 给出了轴向间距为0.1R和0.08R时尾桨总的拉力系数随交叠角变化的曲线图。从图9可以看出，两种间距时尾桨气动力随交叠角的变化趋势整体上是相似的，但是也略有差别。两种间距时，交叠角为45°时垂直于旋转面的拉力系数均是最大的。在交叠角45°之前时，拉力系数变化趋势都是呈上升的，增长的速率较接近。0.1R间距的气动力明显是要大于0.08R间距的气动力。45°之后两组数据都减小，二者在减小的速率上有差别。

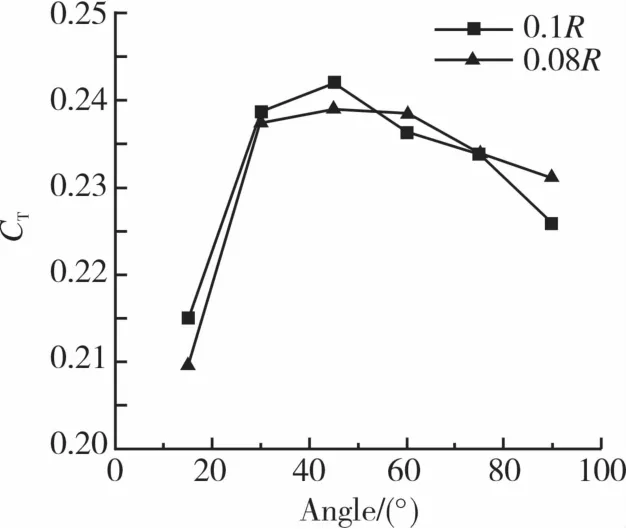
图9 0.1R，0.08R间距下尾桨气动力随角度变化对比图Fig.9 Comparison diagram of the aerodynamic changes of the tail rotor with the angle at vertical space of 0.1R and 0.08R

图10 给出了间距分别为0.1R与0.08R的尾桨上下桨叶的气动力对比图（上面的桨叶标识为L－1，下面的桨叶标识为L－2）。从图10可以看出，不管是间距为0.1R还是0.08R的尾桨，桨叶L－1的升力随着交叠角的增大而增大，桨叶L－2的升力在30°附近之前随着交叠角的增大而增大，30°之后桨叶L－2的升力随着交叠角的增加而减小。

图10 0.1R，0.08R间距时上下桨叶气动力对比图Fig.10 Aerodynamic contrast diagram of upper and lower blades at the space of 0.1R and 0.08R

出现这种现象的原因可以用桨－涡干扰来解释。图11和图12分别给出了两种间距时不同交叠角的涡量图。当尾桨的交叠角为15°～45°时，可以看出尾桨L－2的桨尖涡干扰另一边的尾桨L－1周围的流动，而尾桨L－1距离尾桨L－2较远，所以尾桨L－1的桨尖涡对尾桨L－2的干扰较小。在交叠角为15°时该现象最为严重，随着角度的增大，干扰现象减弱，拉力随之上升。当交叠角为45°～90°时，由于不同侧的L－1与L－2之间的角度减小，此时尾桨L－1的桨尖涡对尾桨L－2的干扰明显增强，而尾桨L－2与尾桨L－1的距离变大，干扰变小，总体升力随之下降。到交叠角为90°时，前者的干扰现象最为明显。

图11 0.1R间距15°，30°，60°，75°交叠角的尾桨涡量图Fig.11 Vorticity diagram of tail rotor at 0.1R overlapping angles of 15°，30°，60°and 75°

图12 0.08R间距15°，30°，45°，60°，75°，90°交叠角的尾桨涡量图Fig.12 Vorticity diagram of tail rotor at 0.08R overlapping angles of 15°，30°，60°and 75°

分析轴向间距对气动力的影响，得到如下结论：轴向间距变小时，桨叶之间的距离会变得更小。在尾桨运动时，尾桨上下桨叶的桨－涡干扰会增强，所以小间距尾桨的气动力整体上小于大间距尾桨的气动力。

3 侧风状态下剪刀型尾桨气动噪声分析

3.1 气动噪声监测点布置

为计算尾桨在侧风条件下的气动噪声，在计算过程中设置了5个监测点。按照此方式布置的监测点既能够监测到旋转平面的厚度噪声，也能监测到来流所导致的噪声的影响。图13（z轴未画出）总共有编号为1，2，3，4，5的5个监测点，其在图上坐标系的坐标分别为：（3R，0，0），（5R，0，0），（7R，0，0），（5R，R，0），（5R，－2R，0）。R为桨叶的展长，为1.105 m。

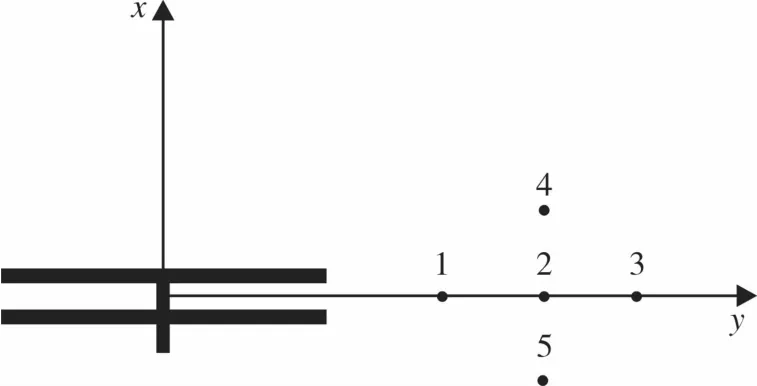
图13 尾桨气动噪声监测点示意图Fig.13 Schematic diagram of aerodynamic noise observation point

3.2 气动噪声求解设置

采用Ffowcs-Williams＆Hawkings噪声模型计算尾桨噪声，然后定义噪声源为剪刀型尾桨的4片桨叶。设置保存噪声数据文件为asd格式，并设置写入频率为2 Hz，每个声学计算所保存的文件要包含100个时间步的计算数据。

3.3 剪刀型尾桨气动噪声特性

图14 给出了间距为0.1R的各交叠角下监测点1的一个周期内的噪声－时间历程图。由图14可知：交叠角较小时，尾桨噪声能量更加集中，其噪声幅值也较大；当交叠角增大时，尾桨噪声能量会逐渐分散直至出现多个噪声峰值，其幅值也会有所降低。

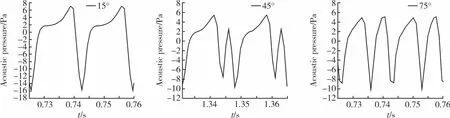
图14 间距为0.1R的各角度下的一个周期内的噪声－时间历程图Fig.14 Acoustic pressure－time history diagramat various angles with a spacing of 0.1R

图15 给出了间距为0.1R的各交叠角下监测点1的噪声－频率图。尾桨交叠角的不同，可以“调制”出多个桨叶通过频率，从而改变了尾桨的噪声频谱，降低了尾桨的噪声水平。尾桨在受到涡干扰的时候脉动减小，并且夹角越小越明显。

图15 间距为0.1R的各角度下的噪声－频率图Fig.15 Sound pressure level－frequency diagram at various angles with a spacing of 0.1R

图16 给出了两种间距时不同交叠角尾桨的5个监测点的气动噪声声压级数据。可以看出：当单独考虑交叠角变化对气动噪声的影响时，剪刀型尾桨的气动噪声在15°～60°的范围内都是随着交叠角的增加而减小，变化趋势较剧烈；当交叠角在60°～90°的范围内时，气动噪声声压级的大小随着交叠角变化的趋势较平稳；轴向间距对噪声声压级的影响不明显。这样的结果显示的趋势与前述的气动力的变化趋势有相似之处，说明尾桨上下桨叶的桨－涡干扰对噪声有很大的影响。

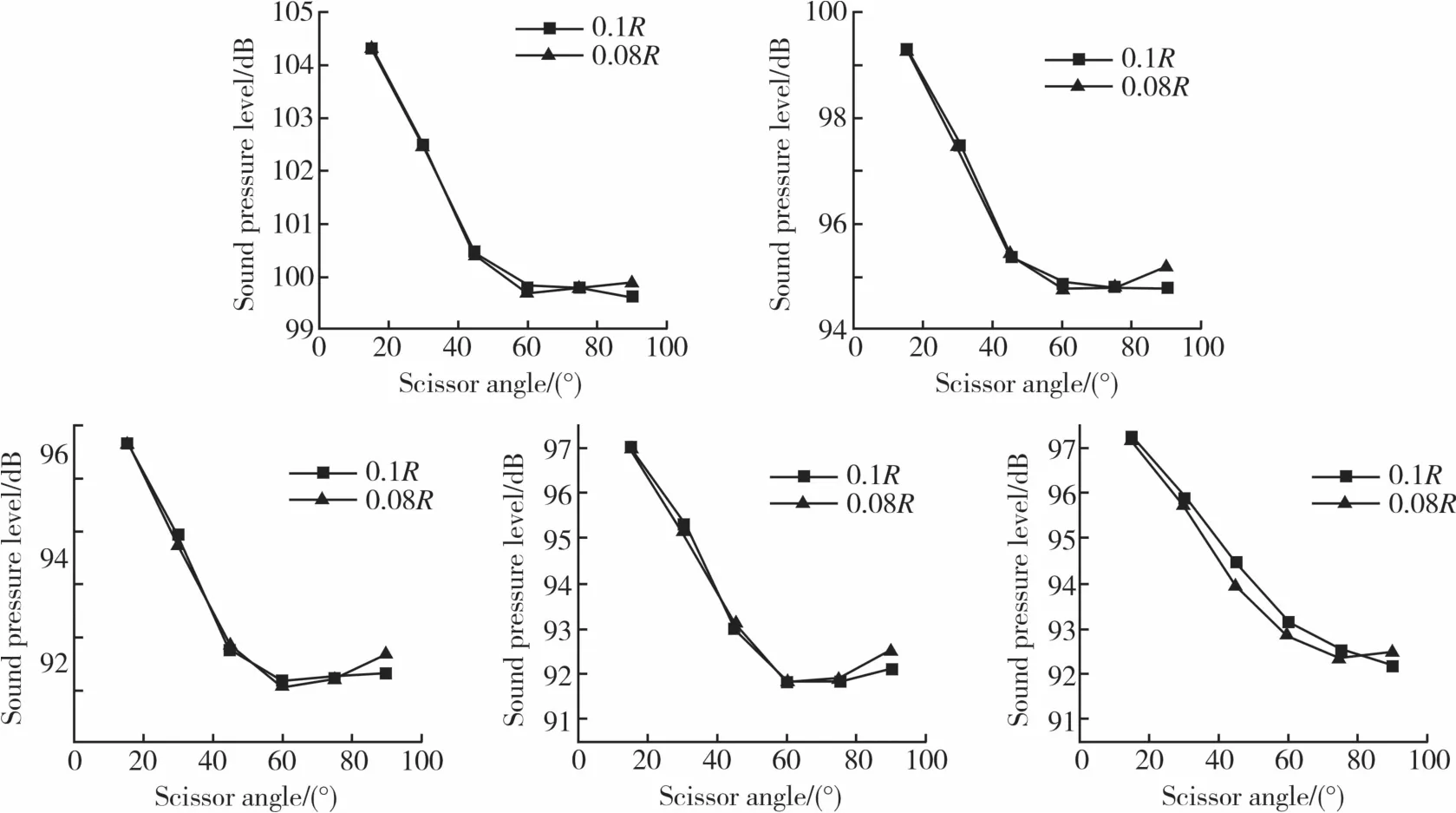
图16 0.1R间距与0.08R间距时的气动噪声对比图Fig.16 Comparison diagram of aerodynamic noise at vertical space of 0.1R and 0.08R

4 结论

本文对剪刀型尾桨的流场进行了计算，分析了其气动力特性，在尾桨流场数据的基础上，进行了尾桨气动噪声计算，得出以下主要结论：（1）尾桨气动力计算结果表明，尾桨的拉力随着交叠角的增大呈现先上升后下降的趋势，45°时的尾桨拉力最大，但45°之后的尾桨拉力整体上大于45°之前的尾桨拉力，说明45°之前的桨－涡干扰要大于45°之后的情况。相比尾桨交叠角对尾桨气动力的影响而言，轴向间距的影响较小，但是依旧可以看出轴向间距变小，导致60°之前尾桨的气动力变小，而在60°之后，尾桨气动力随着间距的变小而变大。（2）尾桨气动噪声分析表明，剪刀型尾桨的气动噪声随着交叠角的增大而减小，在60°之前的减小趋势比60°之后的减小趋势要大，其原因是：在60°之前尾桨的桨涡干扰是尾桨L－2的桨尖涡对L－1的干扰，其对气动力的影响更大，对噪声的影响也较大；60°之后，尾桨L－1的桨尖涡对尾桨L－2的干扰更严重，其对噪声的影响比前者的影响小，变化趋势较为平缓。尾桨轴向间距减小使得在侧风情况下的噪声变小，其原因是：由于间距减小，虽然桨叶的距离更近，但桨叶L－1的桨尖涡对L－2的干扰变小，使得小间距尾桨整体噪声变小。