基于学生个性化的初中数学教学设计与评价

【摘要】本文以《勾股定理》一课为例，从新课导入、探索新知、深化理解、课堂评价四个方面阐述基于学生个体差异展开初中数学教学的途径。

【关键词】初中数学 个体差异 教学设计 《勾股定理》

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2019）10A-0067-02

课堂教学应以学生为主体，鼓励学生自主探究，让不同层次学生的个性及综合能力得到发展。笔者根据多年的教学经验和体会，以《勾股定理》第一课时为例，阐述在初中数学课堂中实施学生个性化发展教学与评价的途径。

一、创设情境，导入新课

有的学生对历史感兴趣，有的学生对探索宇宙感兴趣，有的学生崇拜科学家。教师在导入环节，可以根据不同学生的不同兴趣点，利用多种素材创设情境导入新课。

例如，笔者教学《勾股定理》第一课时的导入如下。笔者首先利用商高的故事引出主题：“3000多年前有一个叫商高的人发现，把一根直尺折成直角，两段连结得一直角三角形，‘勾广三，股修四，弦隅五。这句话的意思是，一个直角三角形较短直角边（勾）的长是3，长的直角边（股）的长是4，那么斜边（弦）的长是5。相信同学们或多或少听说过勾股定理，这节课我们就一起来系统地学习。”接着，笔者进一步激发学生的学习兴趣：“许多科学家正在试图寻找其他星球的‘人，为此向宇宙发出了许多信号。我国数学家华罗庚曾建议，发射一种反映勾股定理的图形，如果宇宙人是‘文明人，那么他们一定能识别这种语言，这个事实可以反映勾股定理的重大意义。”这个环节从不同的角度激发了不同个性的学生的学习兴趣。

二、师生互动，探究新知

教师根据学生的实际情况，设计不同的动手任务让学生动手操作，使得每名学生都能参与活动、得出结果。

（一）让学生画一个两直角边分别为3cm和4cm的直角三角形ABC，用刻度尺量出AB的长。再画一个两直角边分别为5cm和12cm的直角三角形A1B1C1，用刻度尺量出A1B1的长。你是否能发现直角三角形三边的关系？

（二）让学生剪4个大小、形状相同的直角三角形拼起来。利用面积你能发现直角三角形三边的关系吗？

学生在动手实践和逻辑推理等能力方面存在着差异，以上设计针对学生个体让学生自主学习探究。学生探索结果如下。

由活动（一）得到32+42=52，52+122=132。

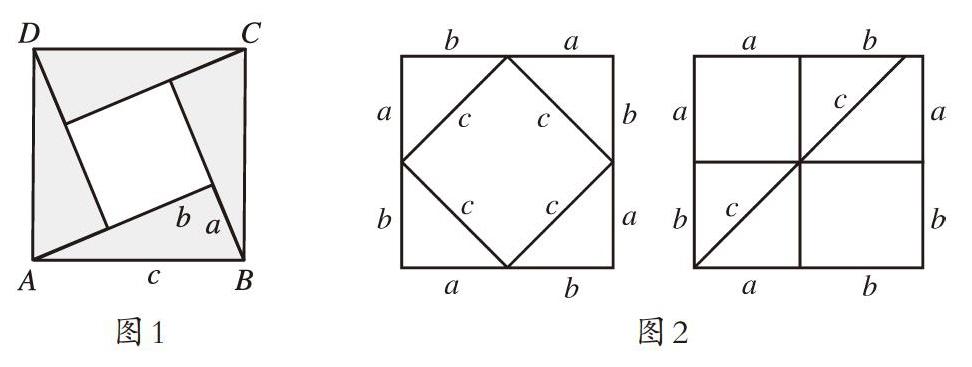
由活动（二）图1得到：S正方形=c2，同时S正方形=2ab+（a-b）2，从而c2=2ab+（a-b）2即c2=a2+b2。

由活动（二）图2得到：左右两边的正方形边长相等，两个正方形的面积相等。于是2ab+c2=（a+b）2化简可得c2=a2+b2。

经统计，班上50名学生，有8名学生根据活动（一）得出结果，25名学生由活动（二）图1得出结果，13名学生由活动（二）图2得出结果，还有4名学生没有得出结果。可见，“条条大路通罗马，成功的道路千万条”;教师不仅要培养学生的动手能力，还要培养他们的逻辑思维能力;教师要鼓励学生敢于直面困难、克服困难，要自信，要积极与老师或其他同学交流。

三、运用新知，深化理解

教师针对学生的情况设计或选取练习题，让学生在解答练习题中运用新知、深化理解。

（一）在Rt△ABC中，已知∠B=90°，AB=6，BC=8，求AC。

（二）Rt△ABC的斜边AC比直角边AB长2cm，另一直角边BC长为6cm，求AC的长。

（三）在Rt△ABC中，∠C=90°，它的两边长是6和8，则它的第三边长是多少？

（四）一个高4米，宽3米的木框，需在相对角的顶点间加一条加固木板，则木板的长为（）

A. 3米   B. 4米   C. 5米   D. 6米

（五）如图3，△ABC中，AB=13，BC=15，AC=14，求BC边上的高。

（六）如图4，长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则AE的长度为多少？

作业设计由易到难，有效针对不同学生个体，不同学生都能获得发展。

四、课堂反馈，自主评价

一位好教师一定是一位善于评价学生的教师。教师在评价学生时要关注学生的个体差异，发挥评价的激励作用，呵护学生的自尊心和自信心，培养学生的良好习惯以及乐于合作、勇于创新的精神。同时，教师还可以引导学生进行自主评价，不断促进学生的个性发展。

在学生完成作业后的评价环节，笔者抓住学生作业中的闪光点进行肯定性评价，鼓励仍需加强的学生，让作业评价成为师生交流学识、沟通情感的过程，极大地促进学生心智的发展和人格的完善，全面提高学生的综合素质。

为了开展学生评价，筆者设计学生课堂学习自主评价表，让学生从认真、主动、自信、合作交流和思维品质这五个方面各分为A、B、C三个等级进行自主评价，其中“认真”的打分依据为：上课认真听讲，参与活动认真为A，上课能认真听讲，有参与活动为B，上课无心听讲，极少参与活动为C;“主动”的打分依据为：主动预习，主动发言为A，偶尔预习，偶尔发言为B，极少预习，基本不发言为C;“自信”的打分依据为：大胆提问，大胆尝试并表达自己的想法为A，有提问、能尝试表达自己的想法为B，不敢提问、不敢尝试、不敢表达自己想法为C;“合作交流”的打分依据为：善于与人合作，虚心听取别人意见为A，能与人合作，能听取别人意见为B，缺乏与人合作，难以听取别人意见为C;“思维品质”的打分依据为：能有条理表达自己意见，具有创造性思维为A，能表达自己意见，有一定的思考为B，不能准确表达自己意见，不能独立解决问题为C。

德国哲学家、数学家莱布尼茨说过：“世界上没有完全相同的两片树叶。”学生的学习兴趣、分析理解能力、创新能力、学习习惯、学习方式等存在着差异，表现出不同的个性特点。在课堂教学中，教师不仅要关注学生知识目标的达成，还应关注学生学习过程的评价，组织精彩的教学设计、搭建良好的评价平台，关注学生的个性化学习，促进学生的个性化发展，全面提高学生的综合素质。

【参考文献】

[1]张大均.教育心理学[M].北京：人民教育出版社，2005

[2]唐智松.教育原理：研究与教学[M].重庆：西南师范大学出版社，2017

注：本文系重庆市2019年度教育综合改革研究重点课题“重庆市义务教育阶段学生综合素质评价研究”（课题编号：19JGZ06）阶段性研究成果。

作者简介：向国建（1971— ），男，重庆万州人，中学数学高级教师，研究方向：数学学科教学。

（责编 刘小瑗）