纬平棉针织物双向拉伸线圈形态分析
尉腾祥, 李 敏 , 彭虹云, 付少海
(1. 江苏省纺织品数字喷墨印花工程技术研究中心, 江苏 无锡 214122; 2. 生态纺织教育部重点实验室(江南大学), 江苏 无锡 214122)
针织物具有延伸性高,初始模量低,弹性回复性能好和手感松软等特性,常被作为运动服、休闲服、内衣及手套袜类的重要面料。丝光是棉织物前处理过程的重要步骤,通过施加张力和浓碱液处理改变纱线的微观结构,可大幅提高其尺寸稳定性、吸收性能、舒适性和力学性能[1-2]。在丝光或其他工序加工过程中,张力是线圈变形和外部响应行为的决定性因素。针织物拉伸变形是拉伸、剪切、弯曲和压缩等多种力作用的复合。纤维剪切、滑动和弯曲3种变形模式,均表现出多尺度行为[3]。平面拉伸是针织物最基本的变形方式。双向拉伸是指拉伸同时在2个相互垂直的方向上进行;或者织物只在1个方向上拉伸,在与拉伸成垂直的方向上织物的尺寸不变,单向拉伸可认为是双向拉伸的特例[4]。然而,由于针织物是由线圈组成,在受力条件下线圈形态会发生变化,从而引起性能的改变。
目前针织物线圈形变方面的研究主要集中在2个方面。一是建立几何模型来描述松散状态下针织物线圈结构。最初Peirce等[5]假设织物线圈由圆弧和直线构成,并且线圈具有恒定的圆形横截面;在这个假设的前提下,Munden等[6]进行深入研究,认为织物尺寸主要由线圈长度决定,引入了与结构参数有关的方程来确定不同松弛状态下针织物的尺寸稳定性;在此基础上,Mozafary等[7]提出线圈形状的新型网络模型,建立了针织物的三维模型,用来描述针织物的线圈结构。二是研究针织物拉伸变形机制,建立力学模型来模拟织物的拉伸变形。为了解针织物拉伸变形的过程,Duhovic等[8]通过对织物实际加工过程的模拟,分析了织物在加工过程中所产生的力对线圈几何形状的影响;在了解力的变化对线圈形状的影响后,Dusserre等[9]基于梁理论提出了耦合半解析模型来预测平针织物复合材料的拉伸变形和弹性性能。虽然力学模型可以预测针织物的拉伸变形,但是对线圈在拉伸变形过程的变化没有探究,线圈结构参数的变化会影响织物的性能,因此对针织物线圈变化的研究十分必要。
针对上述问题,本文以最常见的横向延伸性大、易变形和脱散的纬平棉针织物为研究对象,探究在不同拉伸张力条件下针织物结构参数(包括圈高、圈距、形态系数、剪切角等)的变化规律,为后续研究丝光过程对纬平针织物线圈形态的影响提供参照。
1 实验部分
1.1 材料与设备
织物采用市售漂白单面棉针织物,其中圈距为0.7 mm、圈高为0.5 mm、线圈长度为0.72 mm、纱线有效直径为0.18 mm。实验丝光架(自制)。
1.2 实验方法
将20 cm×20 cm的漂白单面棉针织物固定在丝光架上,在其中心区域划出14 cm×14 cm的区域,将针织物分为由不同节点组成7 mm×7mm的方形单元,以方形单元作为研究对象,如图1所示。织物在双向拉伸时所受张力的大小用扩幅表示,分别将针织物双向扩幅5%、10%、15%后,绘制位移向量场。

图1 实验丝光架Fig.1 Experimental mercerizing device
1.3 性能测试
测量节点处线圈的圈距、圈高、形态系数、剪切角和节点的位移向量,每个单元测量10次,计算平均值。位移比的计算如式为
式中:p为位移比,%;L0为织物拉伸前长度,m;L1为织物拉伸后长度,m。
剪切角是指织物单元受力后与拉伸方向成的夹角,剪切角α示意图如图2所示。用万能量角器测量角α的大小,每个角度测量10次取平均值,即为线圈的剪切角。

图2 剪切角示意图Fig.2 Diagram of shear angle. (a) Before stretching;(b) After stretching
2 结果与讨论
2.1 向量场与位移场
图3(a)示出不同扩幅条件下针织物的节点向量场。向量的起点和终点分别表示节点初始和变化后的位置,箭头的方向表示节点的位移方向。结果表明:针织物整体变形沿轴向对称,对称中心附近的节点主要以单向位移为主,与对称轴平行节点伴随微小位移;在织物边缘,应力的集中限制了线圈单元的自由运动,使线圈单元发生歪斜等大变形行为。在不同扩幅条件下,各节点的位移大小与方向不同,使得织物不同区域呈现不同的变形。由于载荷沿平面传递,节点的位移向量表现出不同的大小和方向[10]。

图3 不同扩幅条件下织物的节点向量场和位移场Fig.3 Nodal vector field (a) and displacement field (b) of fabric at different tension conditions
图3(b)示出不同扩幅条件下针织物的节点位移场。研究发现,在节点位移场中出现位移比小于50%的区域。在椭圆区域内节点的位移较小;随着扩幅的增加,织物边缘区域节点的位移变大,椭圆面积由占整个织物的39.48%降低到17.36%。该结论表明,随着扩幅的增加,拉伸织物的小位移节点变少。
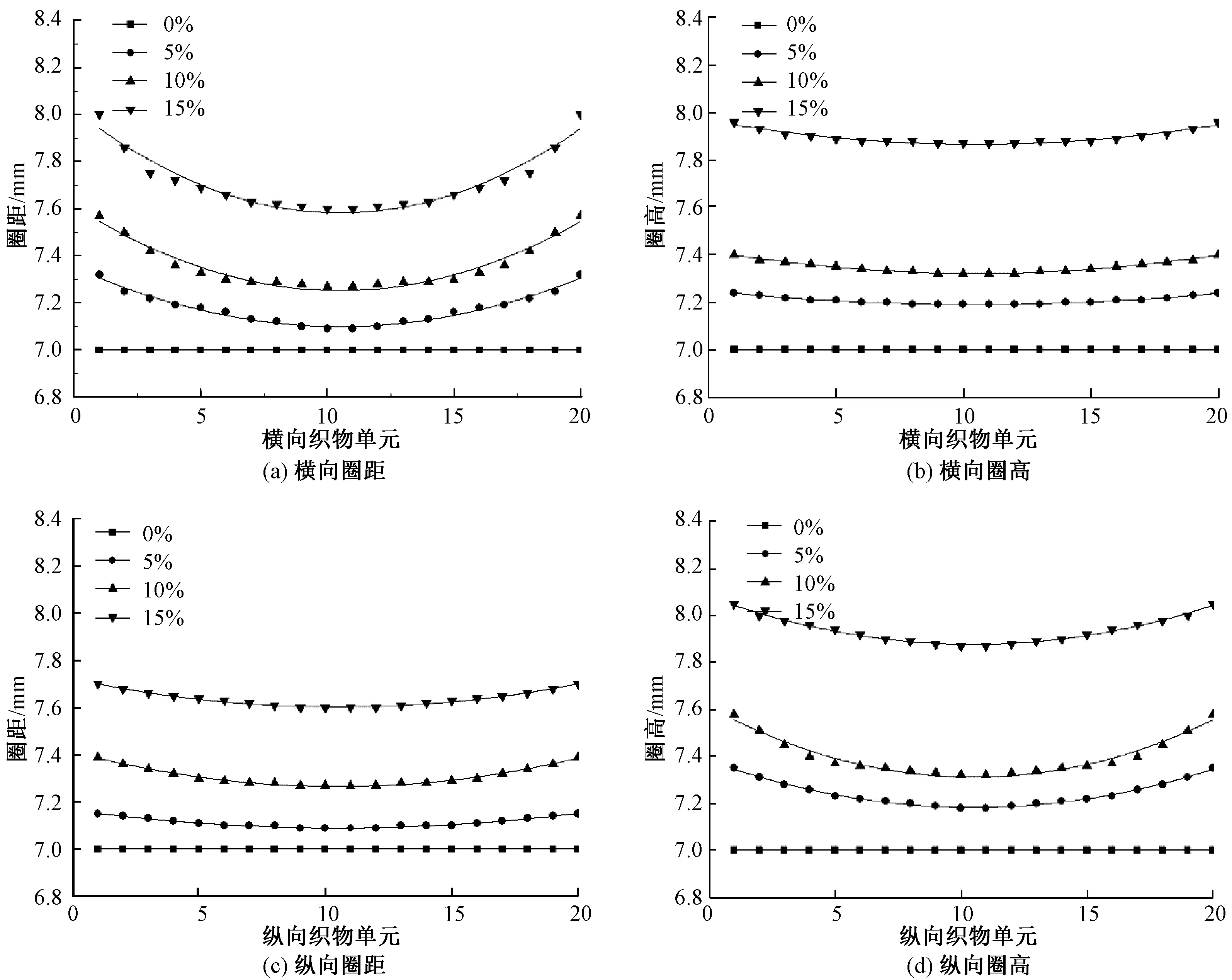
图4 中心线上织物单元横纵向的圈距和圈高Fig.4 Coil spacing and height in horizontal and vertical direction of unit on center line. (a) Horizontal coil spaing;(b) Horizontal coil height; (c) Vertical coil spacing; (d) Vertical coil height
2.2 圈距和圈高
圈距和圈高直接关系到横向和纵向的密度,是决定织物尺寸稳定性的重要因素[9]。图4示出横向和纵向中心线上织物单元的圈距和圈高。
研究发现,圈距和圈高的变化符合抛物线的变化规律,拟合方程和拟合度R2如表1所示,R2均在0.95以上。由图4可知:与未拉伸织物的圈距和圈高相比,经过拉伸的织物中心线圈距和圈高均增加,且越靠近中心点,中心线上织物单元的圈距和圈高越接近未拉伸织物的圈距和圈高;但横向中心线上单元的圈距与纵向中心线上单元的圈高变化幅度较大,这是因为结构单元的初始取向和在横纵方向上线圈的变化能力不同造成横向圈距和纵向圈高受力变化明显[10]。

表1 圈距和圈高的拟合方程Tab.1 Fitting equation of coil spacing and coil height
2.3 形态系数
形态系数由圈高和圈距的比值表示,通常织物受力变形时织物圈高和圈距会随之发生变化,因此采用形态系数可以较好地描述针织物的变形特点[8]。图5示出织物中心线上单元的形态系数。由图可知,未拉伸织物的各单元处形态系数为0.71,经过双向拉伸后中心线上各单元的形态系数均变大。在横向中心线上,越靠近中心点单元的形态系数越大,越靠近边缘形态系数越小;而在纵向中心线上,越靠近中心点单元的形态系数越小,越靠近边缘形态系数越大,并且随着拉伸张力的增加,中心点单元所在的形态系数变化越大。当扩幅达到15%时,纵向中心线上的形态系数变化较小。
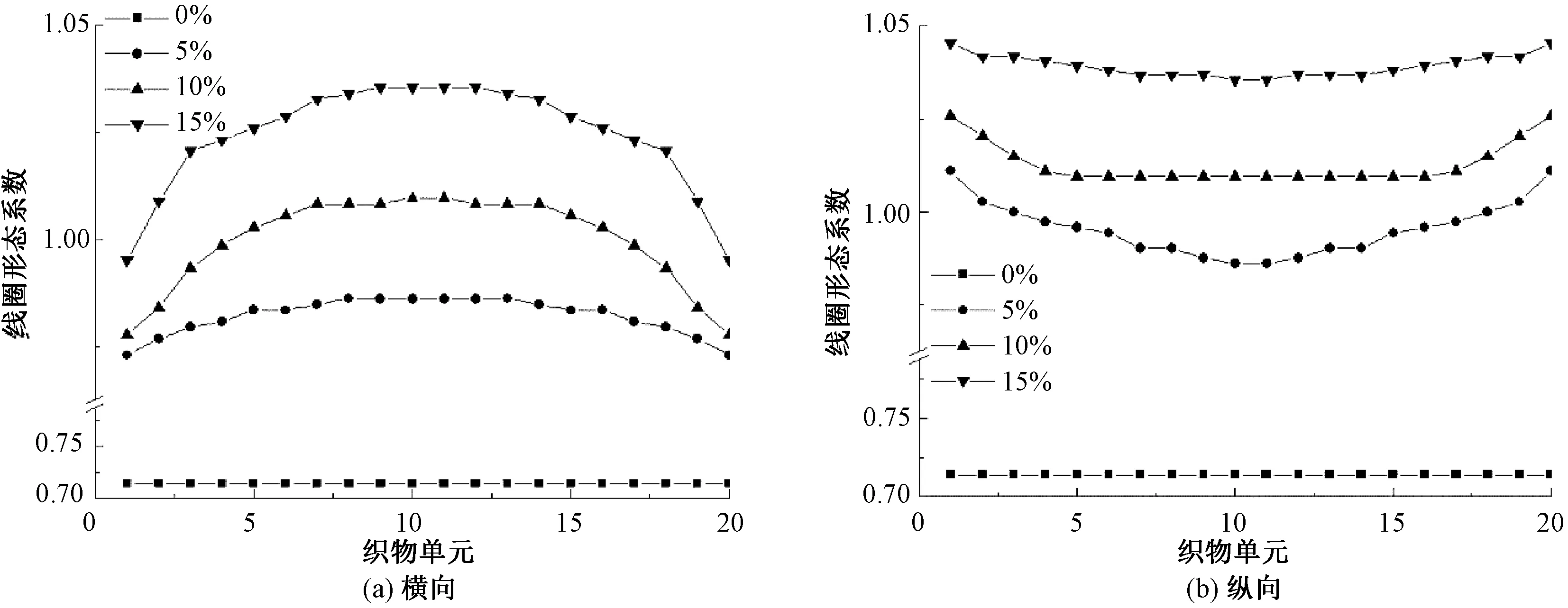
图5 横向和纵向中心线上各单元的形态系数Fig.5 Shape coefficient of each unit on center line in horizontal (a) and vertical (b) direction
图6示出织物所有单元的形态系数。由图可知,沿拉伸方向,织物各节点处的形态系数呈梯度对称分布。在横向方向上,越靠近中心点单元的形态系数越大,越靠近边缘形态系数越小;而在纵向方向上,越靠近中心点单元的形态系数值越小,越靠近边缘形态系数越大。随着扩幅的增加,中心区域线圈的形变增加(如图6中红色和黄色部分)。
2.4 剪切角
图7示出织物不同单元处剪切角的分布。剪切角越小,表明织物单元受力不均衡;剪切角越大,表明织物单元受力比较均衡。

图6 不同扩幅条件下织物所有单元的形态系数Fig.6 Shape coefficient of all units in fabric with different tension conditions

图7 不同扩幅条件下织物所有单元的剪切角Fig.7 Shear angle of all units in fabric with different tension conditions
由图7可知,从织物中心区域到边缘区域,织物剪切角分层明显,存在明显的递变规律,织物的大剪切行为易发生在织物边缘区域。在织物中心区域,剪切角较大,这是因为织物受力比较均衡;在织物边缘区域,剪切角较小,这是因为织物受力不均衡。随着扩幅的增大,织物中心区域剪切角变小(由89.20°减小到88.65°),但是区域面积变大;织物边缘区域剪切角变小(由87.95°减小到86.80°),区域面积变小。研究表明,随着扩幅的增大,织物的最大剪切角变小,并且所有剪切角减小的趋势变缓。
3 结 论
本文研究了在双向拉伸条件下丝光前纬平棉针织物单元的线圈结构变化,以及织物在不同张力条件下织物单元的位移向量、圈距、圈高、形态系数和剪切角的变化规律。研究发现:在双向拉伸的条件下,纬平棉针织物的向量位移场呈对称分布,在x轴和y轴附近主要发生平行于对称轴的单向位移,随着拉伸张力的增加,织物的位移变大,方向发生变化,椭圆面积由占整个织物的39.48%降低到17.36%;圈距和圈高的变化符合抛物线的变化趋势,拟合度在0.95以上;形态系数呈梯度分布,织物单元存在周期性变化;从织物边缘到织物中心,剪切角存在明显的递变规律,随着扩幅的增加,中心区域的面积减小,剪切角的变化趋势变缓。这些研究为以后探究双向拉伸丝光棉针织物线圈变化做了前期的探索,为构建针织物受力变化模型的奠定了基础。
FZXB

