基于非牛顿流体本构方程的熔喷纤维直径预测

孙光武， 李杰聪， 辛三法， 王新厚

(1. 上海工程技术大学 服装学院， 上海 201620； 2. 东华大学 纺织学院， 上海 201620)

熔喷技术是由高温高速气流牵伸熔融聚合物进而一步成纤的纺丝技术，制备出的纤维(一般为1～5 μm)在成网帘上逐渐聚集而形成熔喷非织造布。由于纤维较细，具有较大的比表面积，熔喷非织造布往往被用于制造空气和液体过滤材料、吸油材料等。熔喷非织造布在应用中的表现直接受到其纤维直径的影响，具有较细纤维的熔喷非织造布的过滤性能往往较好。熔喷非织造生产线的工艺参数对熔喷非织造纤维直径具有很大的影响，需要反复调整才可获得最佳的纤维细度，因此，熔喷拉伸理论模型的研究特别是涉及到纤维直径的预测则显得愈发重要。因为其能在理论上预测直径，从而指导实际生产，并能从机制上阐述各工艺参数之间的关系，为商业化生产提供理论依据。

早期的熔喷拉伸理论由Uyttendaele等[1]通过改进熔融纺丝模型得到，这种模型被称为“自由端”纤维-气流模型。因在熔喷技术中气流牵伸纤维，纤维的尾端并无握持力，这与熔融纺丝“非自由端”不同。文献[2-3]将熔喷拉伸模型分别推广至二维和三维空间。各类方法如蒙特卡洛法、龙格-库塔法、有限元法和幂律模型[4]也被广泛用于求解熔喷拉伸模型方程。Sinha等[5]提出一种简单的准一维模型，该模型计算量较小，同时也能精确预测纤维的运动和直径变化。Shambaugh等[6]以静态结晶动力学方程为基础，模拟了熔喷纤维在成纤过程中的结晶变化，该方法成功将熔喷纤维的宏观结构预测与微观结构预测相结合。不同于上述模型，Sun等[7-8]提出了一种基于拉格朗日方法的拉伸模型，通过将纤维假设成由珠子、弹簧、黏壶串联的模型，预测每个珠子的位置和物理性能的变化，进而预测纤维的实时位置和各项性能参数。

熔喷纤维拉伸模型经过多年的发展，从简单到复杂，从一维到三维，目前文献中已报道的模型可预测任意时刻纤维在整个气流场中的位置、温度、速度、直径，甚至结晶度。然而为了简化计算，在模型中采用牛顿流体本构方程或者经典的Maxwell本构方程，这些方程由于难以准确描述聚合物熔体复杂的非牛顿黏弹行为，导致模拟的纤维直径与实际结果差异较大。为此，本文引入4种非牛顿流体本构方程：PTT(Phan-Thien-Tanner)方程、UCM(Upper-Convected Maxwell)方程、Giesekus方程和Rouse-Zimm方程，结合已建立的拉格朗日熔喷拉伸模型[9-11]预测纤维直径，以定量化分析非牛顿流体本构方程对最终纤维直径预测结果的影响[12]，从机制上揭示非牛顿流体的黏弹行为对熔喷纤维的成纤作用。

1 理论模型

拉格朗日方法是一种描述流体运动的基本方法，即对流体质点进行标记，流体质点的空间坐标与物理量就表示为质点及时间的函数。建立熔喷纤维拉伸模型的目的是为了研究熔喷纤维在拉伸过程中的细化规律、纤维内外应力变化、纤维在气流场中的运动情况以及纤维段之间的相互作用。模型的研究对象是纤维片段，其目的是求解出纤维片段的各物理量与空间坐标在流场中随时间变化的规律，而这与拉格朗日方法一致。

图1示出采用珠链模型描述的熔喷纤维。纤维可假设为由珠子和串联珠子的熔体单元(类似链条)组成。

图1 纤维珠链模型Fig.1 Bead-chain model of fiber

在不考虑纤维相互纠缠的前提下，熔体从喷丝孔逐渐细化落至成网帘上，纤维所受到的作用力主要有4种：气流拉伸力、黏弹力、表面张力和重力。其中：气流拉伸力和重力为外应力，主要起推动纤维运动、拉伸并细化纤维的作用；而表面张力和黏弹力属内应力，主要起抵抗纤维拉伸和弯曲形变的作用。由于整体的动力学模型较为复杂，且除黏弹力之外的其他作用力并非本文的研究重点，在此仅列出数理方程，详细推导过程可参见文献[9-11]。

气流拉伸力是纤维在高速流场中受到的主要作用力，气流力的大小直接影响纤维在气流中的运动和最终成纤时的纤维直径。纤维段(i-1,i)上所受到的气流力Fd,i-1,i可以分解成压差阻力Fp,i-1,i和摩擦阻力Ff,i-1,i，有

Fd,i-1,i=Ff,i-1,i+Fp,i-1,i

(1)

(2)

(3)

式中：Cp、Cf分别为压差阻力系数、摩擦阻力系数；ρa为空气密度，其值为1.29 kg/m3；vrt、vrn为纤维相对速度(纤维实际速度与所在位置气流速度的差)沿其轴向和径向的分量，m/s；di-1,i为纤维段(i-1,i)的直径，m；li-1，i为纤维段(i-1,i)的长度，也是珠子i-1与i的间距，m；ft、fn分别为纤维轴向单位向量、径向单位向量。

表面张力与纤维的气流力方向相反，纤维段(i-1,i)的表面张力Fb,i-1,i由下式确定：

(4)

式中：(xi,yi)、(xi-1,yi-1)分别为珠子i、i-1的坐标；b、j为x和y方向的单位向量；θ为纤维表面张力系数，本文取0.7 kg/s2 [1-3]；ki-1,i为纤维段(i-1,i)的曲率。

黏弹力是表征聚合物非牛顿行为的主要作用力，也是本文的重点研究对象。纤维段(i-1,i)的黏弹力Fve,i-1,i[12]可表示为

(5)

式中：ri与ri-1分别为珠子i与i-1的空间位置；N2,i-1,i为纤维段(i-1,i)所受第二法向应力。

根据张量分析原理，在理想拉伸状态下，对于某一纤维段，有N2=τt-τn。其中τt和τn分别为轴向偏应力张量和径向的偏应力张量。在本文研究中，引入4种非牛顿流体本构方程分别计算出4种不同的偏应力张量，进而计算出不同的黏弹力，再结合熔喷纤维拉伸模型预测纤维直径。这4种非牛顿流体本构方程[13]分别为：

UCM方程

(6)

PTT方程

(7)

Giesekus方程

(8)

Rouse-Zimm方程

(9)

张量分解公式

(10)

(11)

式中：Tf,i-1,i为纤维段(i-1,i)的温度，K。在实际计算中，利用有限差分方法计算上述非牛顿流体本构方程，得到4个不同的第二法向应力值，并分别代入式(5)计算黏弹力。

为使整个模型封闭，还需纤维的运动控制方程和能量守恒方程，分别为：

(12)

(13)

式中：g为重力加速度，取值为9.8 m/s2；Cb为黑体辐射系数，取值为5.67 W/(m2·K4)[10]；hi-1,i为纤维段(i-1,i)与周围气流之间的传热系数，取值为0.026 W/(m2·K·s)[10]；ψ为纤维黑度，取值为0.4[10]；Ta,i-1,i为纤维段(i-1,i)周围的气流温度，K；mi-1,i为纤维段(i-1,i)的质量，kg；Si-1,i为参与热对流的纤维面积，m2；Cg为纤维段(i-1,i)的比热容，J/(kg·K)，可依据下式[14]进行计算：

Si-1,i=πdi-1,ili-1,i

(14)

(15)

Cg,i-1,i=366.9+2.42Tf,i-1,i

(16)

式中，ρf,i-1,i为纤维段(i-1,i)的密度，kg/m3。以聚丙烯为例，其密度与温度的经验方程[14]为

(17)

2 算法描述

熔喷纤维拉伸模型在第1节已经建立，在求解时仍缺少计算气流力所必需的流场速度和温度，为此需采用Fluent有限元分析软件模拟熔喷气流场(设置流场入口速度为60 m/s，温度为640 K，模头温度为640 K，出口为标准大气环境)，并导出气流场三维坐标、速度和温度的数值解[7-9]。模型的求解方法可概括为：首先依据纤维段的初始物理参数值，并结合式(13)与各作用力的数理方程分别计算出气流力、表面张力和黏弹力，再依据式(12)求解纤维段的速度与位移，最后依据式(15)求解纤维段的直径。由于采用了4种不同的非牛顿流体本构方程，黏弹力需分别求解4次，以观察直径结果的差异。理论模型的求解过程如下。

步骤1：设置i=2，并赋予纤维段(i-1,i)初始长度为10 mm，初始直径为400 μm，初始温度为640 K。依据式(11)与式(15) ～ (17)计算纤维段的初始黏度、质量、比热容、密度。导入Fluent计算的流场坐标、速度与温度数值解。

步骤2：计算开始。读取珠子i-1和i的空间坐标及其周围的流场温度和速度。根据式(1) ～ (3)计算纤维段(i-1,i)受到的气流力；根据式(4)计算其表面张力；从式(6) ～ (9)中选择一种非牛顿流体本构方程，并根据式(5)计算纤维段(i-1,i)的黏弹力；依据式(13)计算纤维段(i-1,i)的温度；依据式(15)计算纤维段的直径；依据式(12)中纤维段受到的合力的大小和方向，计算珠子i-1和i在Δt时间内(可自行设置Δt值，数值越小则输出数据越多，结果越精确，程序运行越慢；反之则结果精确性较低，程序运行较快)的位移。输出各作用力的值、珠子空间坐标和纤维段直径的计算结果。

步骤3：根据步骤2计算的位移，更新珠子i-1和i到新的位置。

步骤4：判断珠子i与喷丝孔(原点)的距离是否达到给定值(该值可自由设定，越大则纤维越长，计算耗时越久)。如果是，则执行步骤5；反之，返回至步骤2，以计算珠子i-1和i在下一个Δt后的位置。

步骤5：Uyttendaele等[1]提出内外应力一致的“凝固点”用以描述纤维直径停止变化的边界条件。在模型中，本文也采用同样的方法，即判断纤维段受到的气流力与重力之和是否等于黏弹力与表面张力之和。如果是，停止计算纤维段的直径变化；反之，在喷丝孔处加入珠子i+1。赋予系统中新纤维段(i,i+1)相应的初始物理属性。返回步骤2。

由于需要研究4种不同的非牛顿流体本构方程对计算结果的影响，所以模型需进行多次计算，每次计算采用一种不同的本构方程。在综合考虑计算时间与计算机性能的基础上，本文采用400个珠子模拟纤维在流场中的运动和细化程度，程序采用MatLab编程求解。当第400个珠子出现在喷丝孔处时，所有运算停止。

本文研究采用聚丙烯的物理属性作为原料参数，但该模型可模拟几乎所有的熔喷原料及工艺过程，仅需进行相应的修改。如更换其他材料，需获得该材料的黏度、比热容和密度方程，即修改式(11)、(16)和(17)；还需修改物理参数值至合适的值，包括应力松弛时间、传热系数和表面张力系数。若更改其他熔喷工艺条件，可在Fluent模拟气流场时，设置不同的压缩气流速度、气流温度、模头温度和外部气流环境等；同时需依据喷丝孔直径设置纤维的初始直径，依据模头温度设置纤维的初始温度。

3 结果与讨论

3.1 模拟熔喷过程中纤维应力的变化

图2示出纤维与喷丝孔距离z对模拟获得的纤维内外应力的影响。

图2 不同非牛顿流体本构方程得到的纤维应力随z坐标的变化Fig.2 Fiber stress calculated by different non-Newtonian fluid constitutive equations and its variation with z coordinate

本文采用4种非牛顿流体本构方程计算得到4种不同的内应力。由图可知，所有曲线的应力值都是在出现1个峰值后，随z值的增大而逐渐下降。即随着纤维远离喷丝孔，应力值逐渐下降至稳定。在纤维应力值达到最大峰值之前，纤维距离喷丝孔较近，由于喷射的2股高速射流在该区域相互融合形成湍流，导致该区域内纤维受到的各项应力不稳定，此时的曲线波动性较大。同时由于此处的高速射流速度最大，所以产生了最大的气流拉伸应力，纤维受到这种强烈外应力作用需要抵抗拉伸力，故而内应力也达到峰值。随着纤维远离喷丝孔，纤维周围气流速度逐渐衰减，其受到的外应力逐渐下降，内应力也随之下降，然而由于熔融纤维的非牛顿流体黏弹特性，黏弹力会有一定的迟滞，这产生了内外应力的应力差，在图2中体现为外应力曲线与4种内应力曲线在相同z值处的间距。在纤维距离喷丝孔的间距小于约3 cm的区域内，内外应力差较大，这说明该区域内纤维细化程度较大。在间距超过3 cm后，内外应力差逐渐缩小，这说明纤维细化程度逐渐减小。当间距超过5 cm后，内外应力逐渐趋于稳定，这意味着纤维直径也逐渐停止变化。

3.2 纤维直径

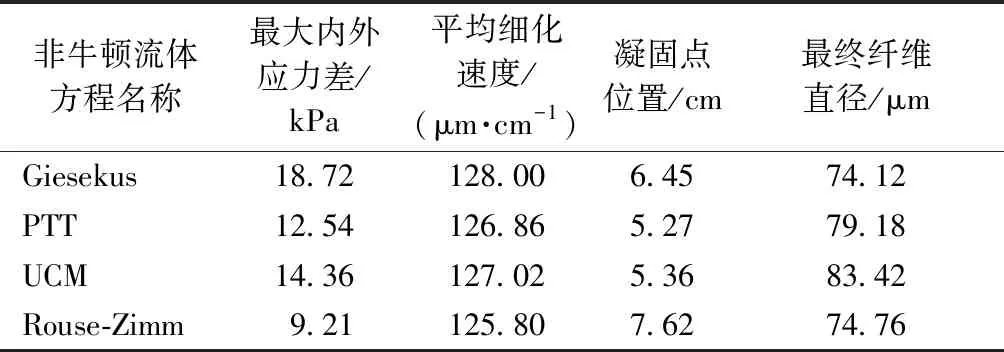
为与Uyttendaele等的在线测量实验进行对比以展示模拟结果的准确程度，在模型中采用了与该在线测量实验相同的工艺条件(具体工艺条件已在第2节说明)，实验与模拟的纤维直径变化示于图3中。为进一步阐明图3中纤维直径的变化机制，表1示出采用4种非牛顿流体本构方程计算获得的指标结果。纤维最大内外应力差是指纤维受到的内外应力差的最大值，是图2中外应力曲线分别与4种内应力曲线之间的最大差值；纤维平均细化速度是图3中纤维直径变化的平均斜率；凝固点位置是指纤维固化时与喷丝孔的间距，在图3中表示为曲线停止变化时对应的z值；最终纤维直径是指纤维经过牵伸后的直径，在图3中表示为曲线尾端z为10 cm处对应的纤维直径。

图3 不同非牛顿流体本构方程得到的纤维直径随z坐标的变化Fig.3 Fiber diameter calculated by different non-Newtonian fluid constitutive equations and its variation with z coordinate

非牛顿流体方程名称最大内外应力差/kPa平均细化速度/(μm·cm-1)凝固点位置/cm最终纤维直径/μmGiesekus18.72128.006.4574.12PTT12.54126.865.2779.18UCM14.36127.025.3683.42Rouse-Zimm9.21125.807.6274.76

由图3可知，Uyttendaele实验结果[1]与模拟结果变化趋势较为相符。纤维自喷丝孔挤出后，其直径变化并不稳定，这是由于喷丝孔附近的气流场形成的湍流所致。随后纤维直径快速下降，这是由于纤维较大的内外应力差所致。从表1可明显发现，纤维细化速度(即曲线在z小于3 cm区域的平均斜率)与内外应力差高度相关，最大内外应力差从大到小排序为：Giesekus > UCM > PTT >Rouse-Zimm，而纤维平均细化速度也有同样的顺序。当纤维与喷丝孔间距z大于3～4 cm时，由于内外应力差缩小，纤维细化速度减缓。间距z超过5～6 cm后，内外应力差稳定导致纤维直径也逐渐趋于稳定。这期间，当纤维达到凝固点时，纤维直径停止变化。采用Rouse-Zimm方程计算得到纤维达到凝固点时距离喷丝孔最远为7.62 cm，而采用PTT方程计算得到纤维达到凝固点时距离喷丝孔最近为5.27 cm。凝固点出现的位置较远可使纤维有充分的空间拉伸，更容易产生较细的纤维。

最终预测的纤维直径从大到小排序为：UCM > PTT > Rouse-Zimm > Giesekus。采用Giesekus方程计算得到的纤维直径更符合Uyttendaele实验结果。所有预测的最终纤维直径均大于实验测量的结果(约60 μm)。这是由于模型中仅考虑了单个纤维段的受力与形变而没有考虑纤维段之间的相互缠结影响。在Bresee等[17-18]的实验观察中，纤维之间明显的接触和缠绕现象会导致纤维直径减小。

4 结 论

本文以熔喷纤维三维拉伸模型为基础，采用拉格朗日方法对纤维在空气中的动力学进行分析，同时结合不同的非牛顿流体本构方程，预测纤维直径的变化情况。虽然模拟结果与实验结果基本相符，但是不同的非牛顿流体本构方程的应用使计算出的黏弹力有差异，从而导致纤维在拉伸形变时内外应力差异的变化。纤维直径的模拟结果显示，纤维的最终直径不仅受到纤维在气流场中的内外应力差的影响，还受到凝固点位置的影响，即：纤维的内外应力差越大，纤维细化速度越快；纤维的凝固点距离喷丝孔越远，则纤维有更加充分的空间进行拉伸，其最终直径也越细。本文的数学模型研究揭示了熔喷纤维的细化机制，同时非牛顿流体本构方程的引入，也成功定量对比分析了熔喷纤维黏弹力学行为的非牛顿性，为熔喷纤维拉伸模型非牛顿方程的选择提供了计算依据。

FZXB