大跨度双曲屋盖分区风压系数研究
孙芳锦,徐中豪,梁 爽
(1. 桂林理工大学 土木与建筑工程学院,广西建筑新能源与节能重点实验室,广西 桂林 541004;2. 辽宁工程技术大学 土木工程学院,辽宁 阜新 123000)
随着各国经济发展和文化进步,各种外型复杂的大跨度结构在国内外屡见不鲜,成为了大跨度结构的发展趋势.大跨度屋盖结构质量轻、柔性大,风荷载是其主要控制荷载.通过对历次风灾调查,发现大跨度建筑结构破坏造成的损失已占总损失的一半以上.目前,关于大跨度屋盖结构的抗风研究主要围绕几种简单体型的屋盖结构,对于具有代表性的复杂体型的大跨度结构研究相对较少,且目前国内外的荷载规范对复杂体型结构的风压系数也尚未给出明确规定.
随着计算机技术和计算流体力学理论的不断发展完善,数值模拟成了继风洞试验之后的大跨度等建筑结构抗风研究的重要手段之一.国内外已有部分学者采用数值模拟技术对结构风压特性开展了研究,并取得了一定成果.国外Murakami等人首次采用大涡模拟方法模拟了立方体周围的三维流场[1],后来又运用大涡模拟方法模拟了德克萨斯科技大学的TTU建筑的风压和风流场,并与现场实测和风洞试验所得数据进行了对比[2].国内陈勇采用数值模拟方法模拟了大跨度悬挑屋盖上的风压分布,并且得出体育场内部流场的规律[3].顾明等利用RANS方法,基于RSM湍流模型对上海铁路南站圆形屋盖上的平均风压进行了数值模拟研究,并把数值模拟结果与风洞试验所得的结果进行了比较[4].汪丛军等模拟了越南国家体育场大跨度屋盖的平均风压和周围风环境的影响[5].孙瑛对大跨度典型屋盖进行了数值模拟研究[6].孙芳锦等人对大跨度柔性屋盖的风振进行了数值模拟的研究[7],并介绍了一种计算流体和结构之间流固耦合作用的强耦合方法.陈亚楠利用标准k-ε模型对体育场大悬挑屋盖表面风压进行数值模拟[8],并分析了风向角、屋盖坡度等因素对环状悬挑屋盖风压分布的影响.
综上,目前大跨度复杂屋盖结构风压特性研究的问题在于大部分研究只针对某一特定屋盖形状,对其复杂体型的风压分布特性研究较少,缺少普遍性的研究结论.且现行国内外规范对复杂形状结构的风压系数尚未给出明确规定[9],给复杂大跨度结构的抗风设计带来不便并造成一定安全隐患.为此,本文选取四种典型投影形状的大跨度双曲屋盖,深入研究其风压分布特性进行,得到了一般性结论,并给出各屋盖的分区风压建议值,对类似屋盖结构的工程抗风设计提供了更准确的理论支持和实际参考.文章首先研究不同影响参数对各屋盖风压分布的影响规律,再选取各屋盖的最不利影响参数,分析给出各形状屋盖的风压系数分区建议值.
1 CFD数值模拟
1.1 计算模型和计算域的选取
本文选取四种典型形状的大跨度双曲屋盖作为计算模型[10](见图1),选取1,2两个测量方向(图2),详细计算参数见表1.经多次试算对比分析,取计算域为20L2×10L1×10Hmax,模型中心位置(0.5L2,0.5L1,0),与x、y和z轴对应.将模型放置在距计算域入口前沿1/3处,即W1=7L2,W2=12L2,计算域满足阻塞率小于3%的要求.

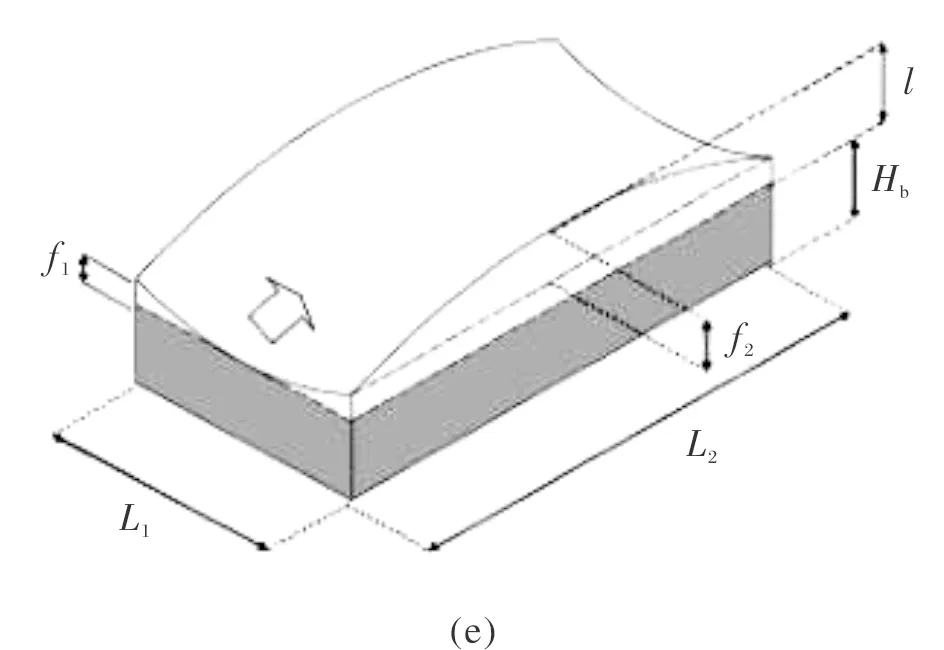
图1 双曲屋盖的几何模型及各相关参数的定义图Fig.1 The geometry models of large-span hyperbolic roofs and parameter definition

图2 风向及测量方向示意图Fig.2 Wind direction and measurement direction
1.2 划分网格
采用六面体结构化网格进行网格划分(见图3),对计算模型附近的网格局部加密,并设置了网格增长因子来使网格大小自计算模型朝外均匀增加,其中网格的最小尺寸设置为0.005 m,网格数量约为180万.

表1 计算模型尺寸表
注:表中ρ=H/Lmax;δ=Hb/Lmax;Lmax=80.00 cm.
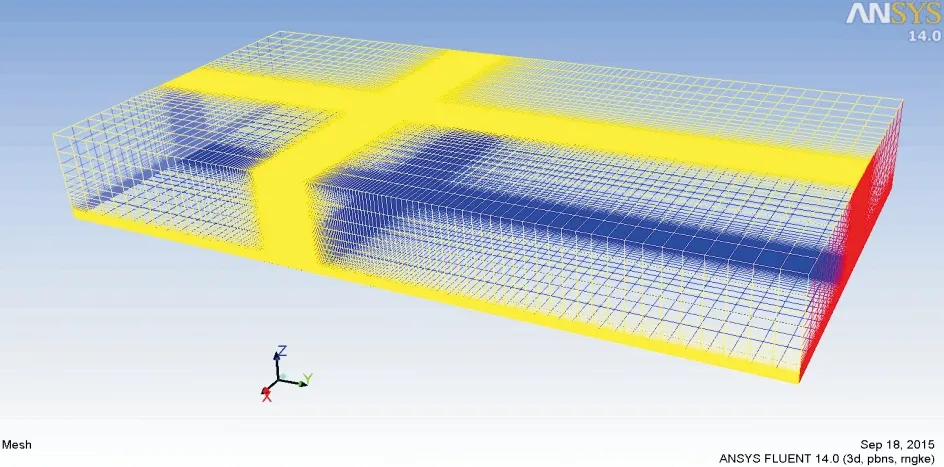
图3 计算模型网格划分图Fig.3 Computational model meshing
1.3 确定边界条件
入口边界条件:为与实验数据比较,选择了速度入口边界条件,并参照文献[10]设定其相关参数.出口边界条件:采用完全发展出流边界条件.壁面边界条件:流体域的顶部和两侧选择自由滑移壁面;建筑物的表面和地面采取了无滑移的壁面边界条件.
2 流场参数对屋盖表面风压分布的影响
2.1 风向角
采用P1模型进行数值模拟计算,地面粗糙度α为0.16,计算域尺寸见1.1节,风速取16.7 m/s,分别选取0°、45°、90°风向角.不同风向角下屋盖表面的平均风压系数分布示意图见图4.
通过分析图4可以得出如下结论:


图4 平均风压系数分布示意图Fig.4 Schematic diagram of average wind pressure coefficient distribution
(1) 在不同风向角作用下,屋盖表面平均风压系数的分布规律大致相同:平均风压系数均为负值,风荷载表现为风吸力,且较大值主要分布在屋盖迎风前缘,距离迎风前缘越近,平均风压系数的变化梯度也越大,随着与迎风前缘的远离,平均风压系数的变化相对平缓.
(2) 无论风向角如何,建筑物的绕流特性类似,均为在屋盖迎风处气流分离的最严重.在凹立面一侧气流分离强度大,风压变化梯度大,风压减小的快,在凸立面一侧气流则与之相反.
(3) 在不同风向角下,屋盖表面平均风压系数最小值所处的位置不同:风向角小于45°时,在建筑物的出流边缘出现最小值;而当风向角大于等于45°时,在屋盖沿气流方向的3/4处出现最小值,位于出流边缘前靠近凹立面的一侧.从图中不难看出,0°风向角是风压分布的最不利情况,其次是90°和45°.
2.2 地面粗糙度
对P2模型进行数值模拟,地面粗糙度α为0.16、0.28和0.4,分别对应三种不同地形,详细参数见表2.屋盖表面的平均风压系数分布示意图见图5和图6.

表2 数值试验工况的试验参数
分析图5和图6中六种工况的数值模拟结果,得出结论如下:
(1)上述的三种不同地形工况中,双曲屋盖的表面风压分布规律非常相似,地貌对其表面风压分布的影响较小,其微小差异主要体现在沿气流流动方向.
(2) 在0°风向角下,地貌对其迎风前缘的风压分布的影响相对较大,随着地面粗糙度增大,其风压系数减小的越慢,说明气流的分离作用随地面粗糙度增大而减小.
(3) 在90°风向角下,大跨度双曲屋盖迎风前缘的风压分布受地面粗糙度的影响不明显,而地貌对其风压分布的影响主要体现在屋盖后方的出流处.随着地面粗糙度的增大,屋盖后方的风压系数减小的逐渐变慢,气流的再附作用也越大.
(4)相对于风向角,地面粗糙度对其屋盖表面风压分布特性的影响较小.


图5 0°风向角下平均风压系数分布示意图Fig.5 Distribution of average Cp at 0° wind direction angle
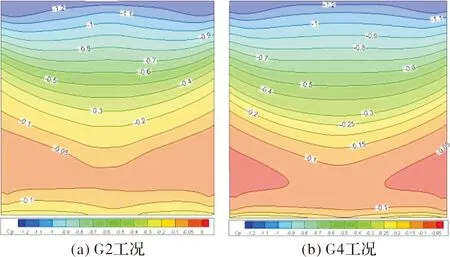
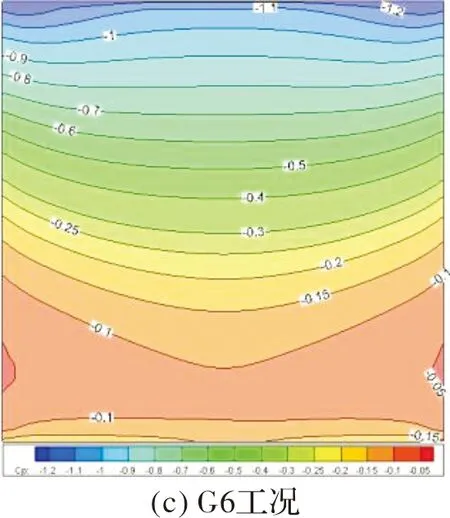
图6 90°风向角下平均风压系数分布示意图Fig.6 Distribution of average Cp at 90° wind direction angle
3 几何模型参数对屋盖表面风压分布的影响
分析在0°这个最不利风向角下,曲率比γ、矢跨比ρ和高跨比δ对高度在20~40 m之间的常见大跨度双曲屋盖结构表面风压分布的影响,其中,L1=L2=80 cm,ρ=H/Lmax,δ=Hb/Lmax;γ=f2/f1.计算域的大小、网格划分、边界条件及相关参数的设置均参照1.1节.
3.1 双曲屋盖两方向的曲率比
为使大跨度屋盖满足相关的力学要求,γ值宜选取在0.43~2.23内,故选取四种有效的γ值0.5、1、1.5、2,来研究曲率比对其表面风压特性的影响.其中Hb=13.33 cm,H=8 cm,计算模型的尺寸详见表3.
表3 计算模型尺寸表
Tab.3Computingmodelsizetable

模型δρf1/cmf2/cmγP11/61/102.675.332P51/61/103.24.81.5P61/61/10441P71/61/105.332.670.5
通过对图7中不同曲率比数值模拟结果的对比,得到结论如下:
(1)分析图7(a)发现,沿气流的流动方向(1方向),在屋盖前1/4中,随着曲率比的减小,平均风压系数值逐渐增大;而屋盖后3/4的变化规律与之相反,随着曲率比的减小,风压系数值也减小.分析图7(b)发现,垂直于气流流动方向(2方向),随着双曲屋盖的曲率比的减小,其风压系数也随之减小.这是由于随着屋盖的曲率比减小,屋盖前缘漩涡脱落随之减少,气流的分离、再附也变小.


图7 屋盖表面平均风压系数对比曲线Fig.7 Average wind pressure coefficient comparison curve
(2)屋盖曲率比不同,其表面风压系数曲线的变化趋势相同,而曲率比变化对风压分布有数值上的影响,其中对屋盖中间的风压分布作用较大.
(3)随着曲率比减小,双曲屋盖表面风压系数受曲率比变化的影响增大;反之随着双曲屋盖曲率比的增大,对其风压系数的作用趋于平缓.当曲率比为2时,屋盖表面的风压系数最大,γ=2是大跨度双曲屋盖的最不利曲率比.
3.2 矢跨比
双曲屋盖的矢跨比ρ=H/Lmax(其中,H=f1+f2),大跨度双曲屋盖结构工程实际中的矢跨比多为1/10~1/5之间,本文采用1/6、1/7、1/8、1/9和1/10这五种有效的ρ值来研究矢跨比对大跨度双曲屋盖表面风压分布特性的影响.其中Hb=13.33 cm,δ=1/6,计算模型的几何尺寸详见表4.
表4 计算模型尺寸表
Tab.4Computingmodelsizetable

模型ρH /cmf1/cmf2/cmHmax/cmP11/108.002.675.3321.33P81/98.892.965.9322.22P91/810.003.336.6723.33P101/711.433.817.6224.76P111/613.334.448.8926.66
通过对图8中不同矢跨比数值模拟结果的对比,得到结论如下:
(1)分析图8(a)发现,沿气流的流动方向(1方向),平均风压系数值以屋盖的0.15 m为界,在0.15 m之前,其值随双曲屋盖矢跨比的增大而减小;分析图8(b)发现,垂直于气流流动方向(2方向),随着双曲屋盖的矢跨比的增大,其风压系数也随之增大.这是由于随着屋盖矢跨比的增大,屋盖前缘处漩涡脱落随之增多,气流的分离和再附作用也越大.
(2)屋盖矢跨比不同,其表面风压系数曲线的变化趋势相同,而矢跨比变化对风压分布有数值上的影响,其中对屋盖中间的风压分布作用较大.
(3)随着矢跨比增大,双曲屋盖表面风压系数受矢跨比变化的影响随之增大;反之随着双曲屋盖矢跨比的减小,对其风压系数的影响趋于平缓.

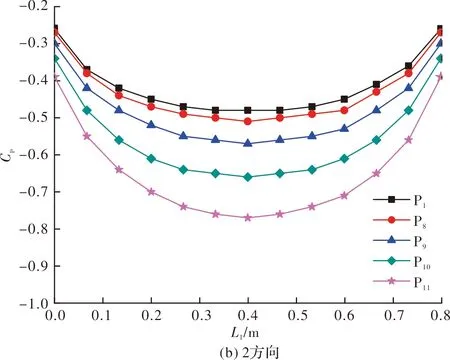
图8 屋盖表面平均风压系数对比曲线Fig.8 Comparison curve of average Cp on roof surface
3.3 底座的高跨比
底座的高跨比δ=Hb/Lmax,本文选取1/6、1/5、1/4和1/3这四种有效的δ值来分析高跨比对大跨度双曲屋盖表面风压分布特性的影响.其中H=8 cm,ρ=1/10,计算模型的详细尺寸见表5.
表5 计算模型尺寸表
Tab.5Computingmodelsizetable
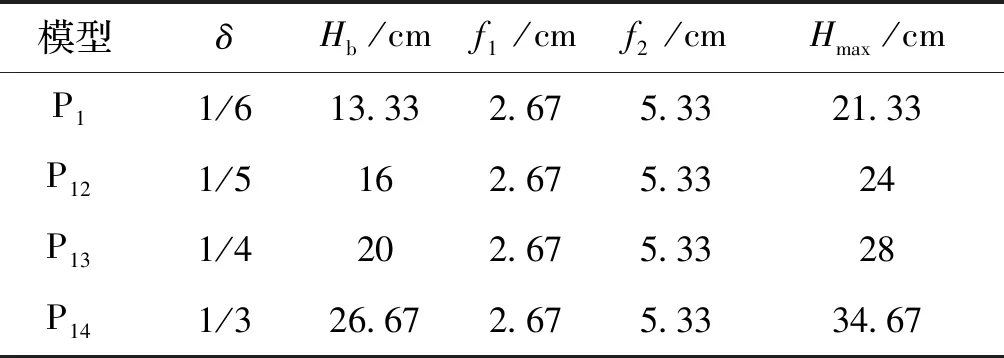
模型δHb /cmf1/cmf2/cmHmax/cmP11/613.332.675.3321.33P121/5162.675.3324P131/4202.675.3328P141/326.672.675.3334.67


图9 屋盖表面平均风压系数对比曲线Fig.9 Comparison curve of average Cp on roof surface
通过对图9中不同高跨比数值模拟结果的对比,得到结论如下:
(1)分析图9(a)发现,沿气流的流动方向(1方向),随着高跨比的增大,双曲屋盖的平均风压系数在其迎风前缘增大明显,而当气流流过屋盖中间之后,平均风压系数值基本趋于平稳,受高跨比影响较小;分析图9(b)发现,垂直于气流流动方向(2方向),随着双曲屋盖的高跨比的增大,其风压系数也随之增大.随着高跨比的增大,双曲屋盖的平均风压系数值在屋盖前半部分减小变快,由此得出:随着高跨比增大,屋盖前缘的漩涡脱落增多,气流分离也随之增大.
(2)相对于矢跨比,屋盖表面风压分布受高跨比的影响较弱.不同高跨比模型屋盖表面平均风压系数曲线的大体趋势相同,底座的高跨比对大跨度双曲屋盖表面风压分布的影响很小,但屋盖迎风前缘受到高跨比的影响很大,而屋盖的后半部分风压分布基本上不受高跨比影响.
(3)随着底座的高跨比增大,其变化对屋盖表面平均风压系数的作用增强;反之,其变化对屋盖表面平均风压系数的作用趋于平缓.
4 平均风压系数的合理建议值
本文在上述研究的基础上,选择最不利风向0°,最不利曲率比γ=2,矢跨比和高跨比为最值的模型展开研究.
4.1 方形双曲屋盖平均风压系数分区建议值
以方形投影面的大跨度双曲屋盖结构作为研究对象,计算模型取P1、P2、P11、P14、P15、P16、P17P18,补充尺寸见表6.
表6 计算模型尺寸表
Tab.6Computingmodelsizetable

模型L1/cmL2/cmρδHmax/cmf1/cmf2/cmP1580.0080.001/61/340.004.448.89P1640.0080.001/61/626.664.448.89P1740.0080.001/101/334.672.675.33P1840.0080.001/61/340.004.448.89
沿气流流动方向,将双曲屋盖表面均匀分成a、b、c、d、e五列,在每列上均匀选取13个测点,分布详情见图10.本文采用拐角是直角的平屋盖为参照,选用了风作用部分比较权威的欧洲规范[11],规范中明确给出了屋面分区图(见图11)以及各区域的风压系数(见表7,表中Cp为平均风压系数,Cp,m为极值风压系数).

图10 方形双曲屋盖表面压力测点分布图Fig.10 Square hyperbolic roof surface pressure measuring point distribution map
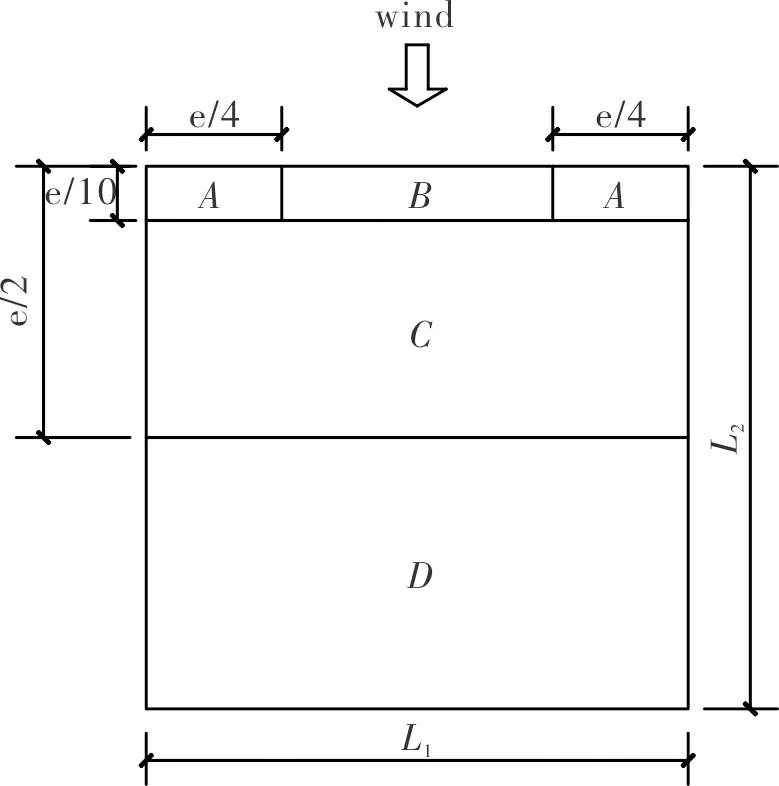
图11 平屋盖分区图Fig.11 The zoning maps of flat roof

ABCDCpCp,mCpCp,mCpCp,mCpCp,m-1.8-2.5-1.2-2.0-0.7-1.2+0.2/-0.2
读取数据并建立以平均风压系数为纵坐标,无量纲函数y0/L2为横坐标的坐标系,得到不同模型的平均风压系数曲线以及其相应的包络线(见图12).然后按照大跨度双曲屋盖表面平均风压的分布规律划分屋盖,确定各区的平均风压系数,并与规范中平屋盖对比.
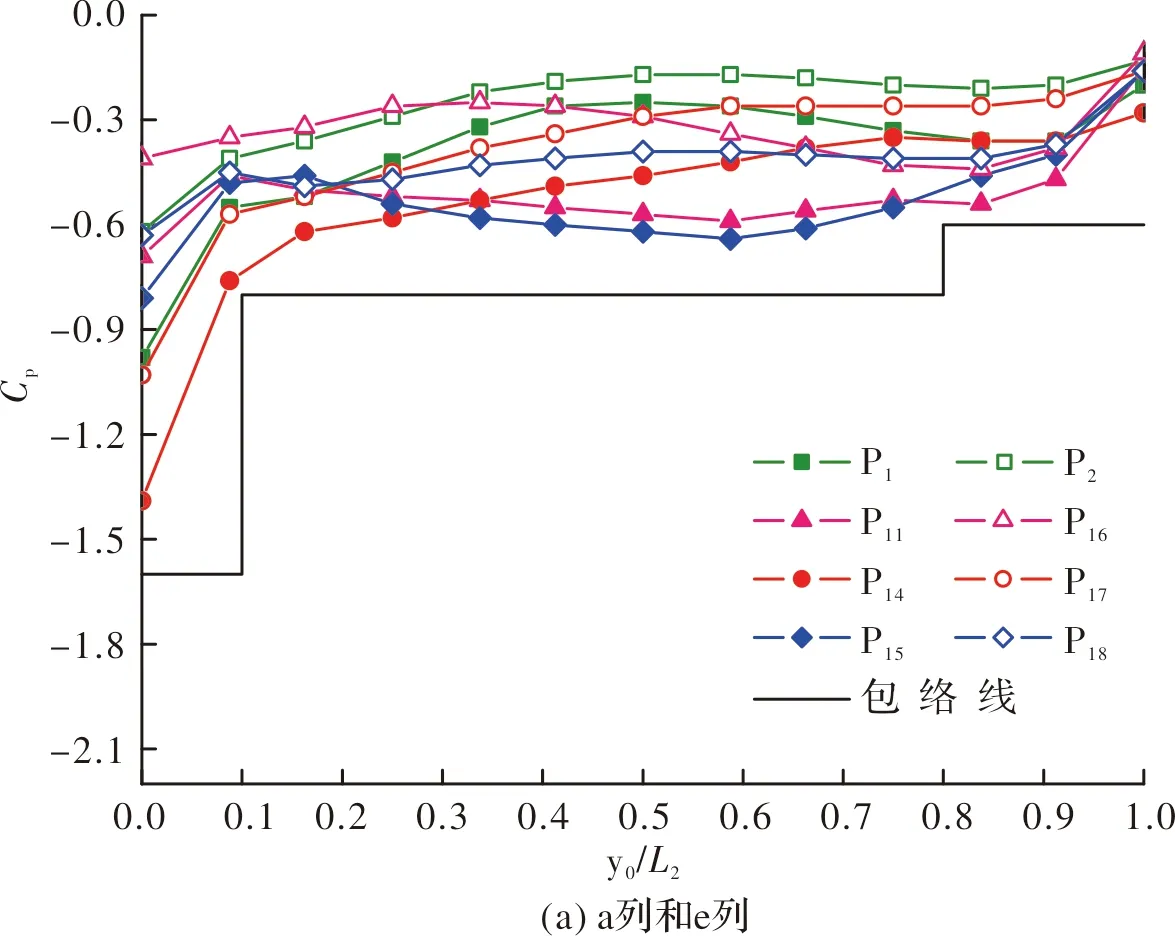
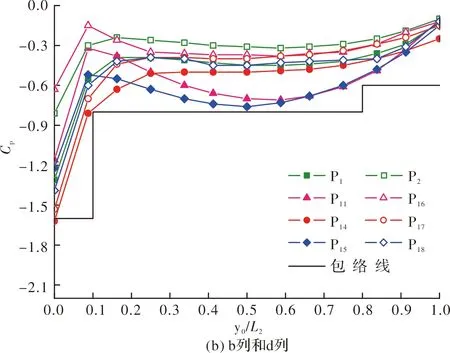
图12 平均风压系数曲线图Fig.12 Average wind pressure coefficient curve
通过图12可以看出,图12(a)和图12(b)的包络线相同,图12(c)的包络线的前方与前两个有较大差别,后面同前两个相同.另外,由于图12中的包络线的包含度超过90%,能确保基于包络线值设计的安全性,故根据包络线的变化给出屋盖表面各区域的平均风压系数,并且为确保其偏于安全,在相邻两列中间区域取较大值,将其绘制成图13a.根据规范中的屋盖分区方式及各区域的平均风压系数值绘制成图13(b).
分析图13,得到结论如下:
(1)方形双曲屋盖的风压分布和规范中的平屋盖有相同规律,其风吸力较大区域都出现于其迎风前缘,随着气流不断向屋盖后方发展,平均风压系数逐渐变小.
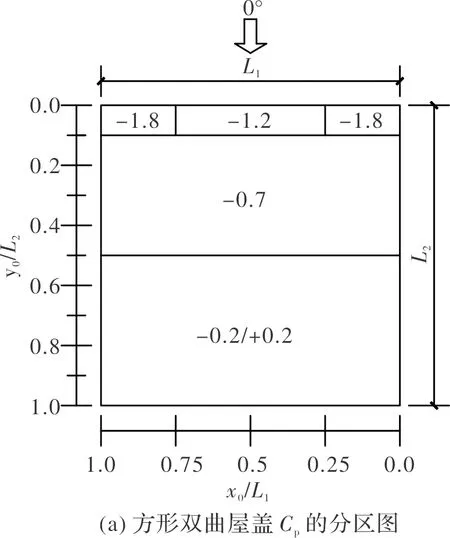

图13 平均风压系数的分区对比图Fig.13 Partition comparison chart of average wind pressure coefficient
(2)方形双曲屋盖表面平均风压系数值全部为负值,说明其表面的风荷载都表现为风吸力作用;而平屋盖后方平均风压系数可为正值,故它不仅仅受风吸力,或许还受风压力作用.
(3)由于双曲屋盖迎风前缘两侧气流的分离作用较强,有较多漩涡脱落,其最大风压出现在迎风前缘的中间区域;而平屋盖正好与之相反,因其迎风前缘中间气流分离作用较强,漩涡脱落的较多,其最大风压出现在屋盖迎风前缘两侧.
(4)双曲屋盖在yo/L2=0.1、yo/L2=0.2、yo/L2=0.8处其值发生突变,风吸力作用逐渐减小,而平屋盖只在yo/L2=0.1和yo/L2=0.5处发生突变.
(5)双曲屋盖中超过95%的区域高出规范中给出的平屋盖的平均风压系数值,且有60%区域的相差率达65%以上.
综上分析,双曲屋盖表面风压分布同平屋盖相比存在较大差异,且整体较平屋盖表面风压系数值偏大.本小节得出的方形双曲屋盖表面平均风压系数的分区建议值不受尺寸限制,适用于高度在20~40 m范围内的方形投影面的双曲屋盖的结构抗风设计.
4.2 圆弧形双曲屋盖平均风压系数分区建议值
采用研究对象为圆弧形投影面的双曲屋盖.其中,圆形双曲屋盖(P3、P19、P20、P21):L1=L2=80 cm;椭圆形双曲屋盖(P4、P22、P23、P24):2L1=L2=80 cm.计算模型的尺寸见表8.

表8 计算模型尺寸表
屋盖表面压力测点的分布详情见图14(参照上节),得到不同模型的平均风压系数曲线以及其相应的包络线见图15,各区域的平均风压系数建议值见图16.

图14 圆弧形双曲屋盖表面压力测点分布图Fig.14 Curved point distribution map of arc-shaped hyperbolic roof
通过图15可以看出,虽然横坐标的取值范围不同,但和方形双曲屋盖一样,图15(a)和图15(b)的包络线是相同的.但图15(c)包络线不仅前方同前两个不一样,而且后方较前两个也存在较大的差别,屋盖前缘最大风压系数较方形双曲屋盖的有所减小,在屋盖后方yo/L2在0.8~1.0范围内,屋盖表面风压系数出现了正值,因此此部分包络线不仅要考虑负值,也要将正值考虑进去.图中包络线的包含度超过95%,能确保基于包络线值设计的安全性.故本节根据包络线的变化给出了圆弧形双曲屋盖各区的平均风压系数的合理建议值,并且为确保其偏于安全,在相邻两列中间区域取较大值,将其绘制成图16.
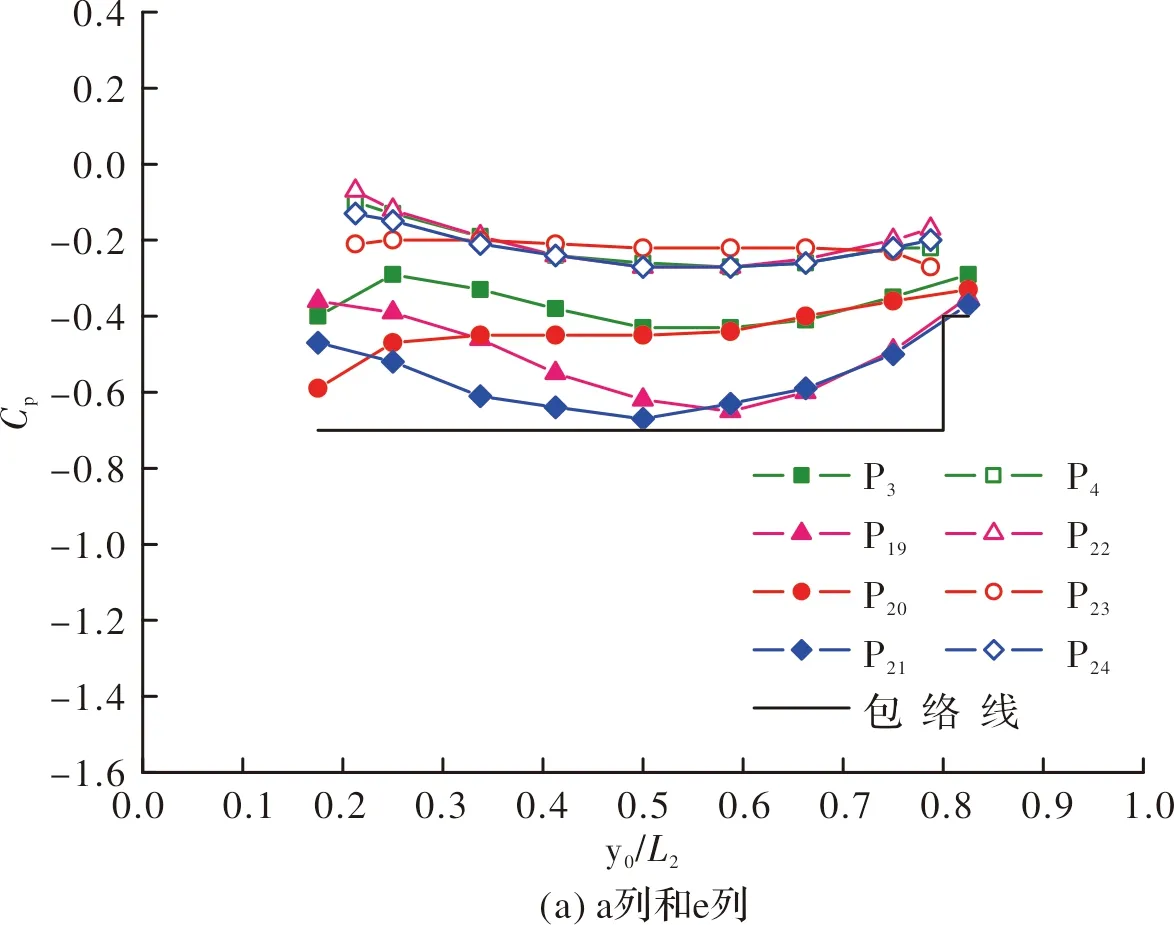

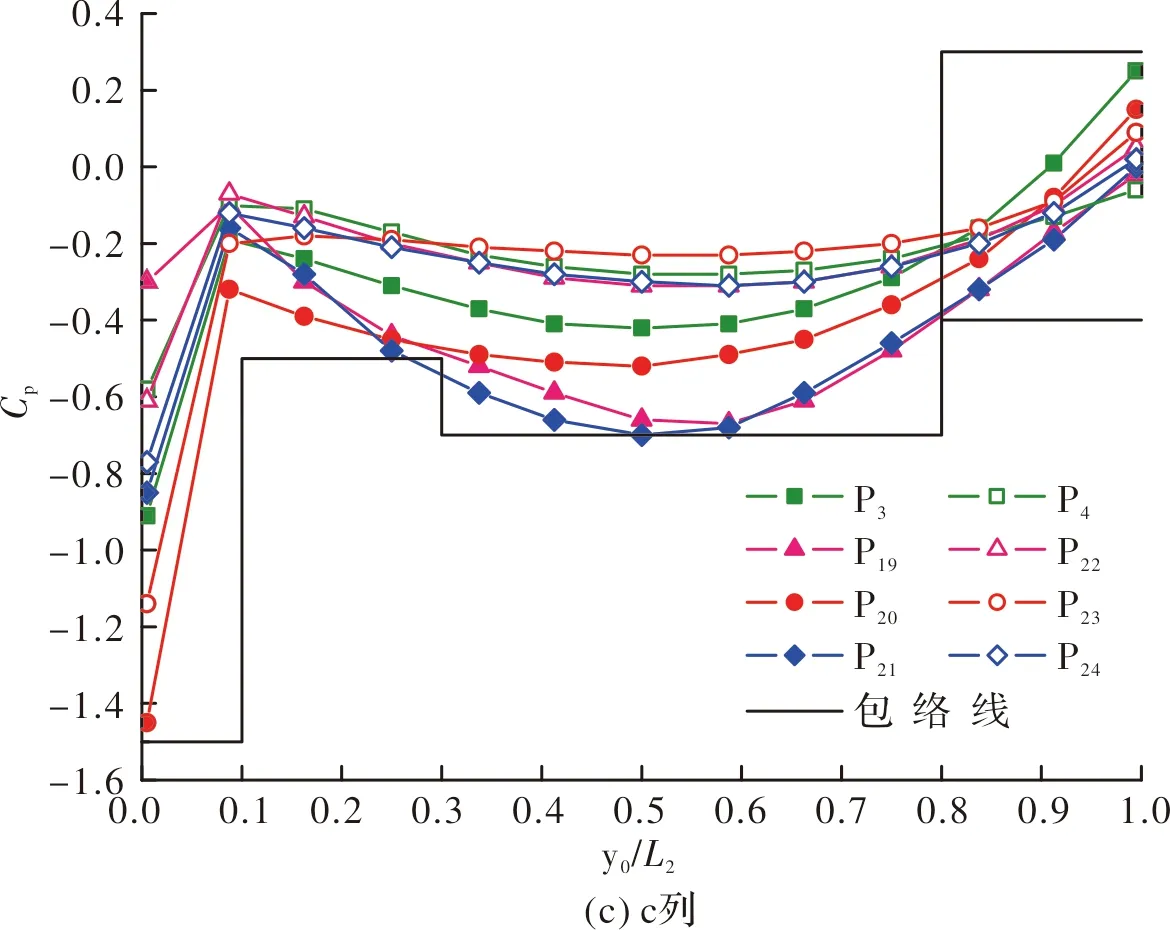
图15 平均风压系数曲线图Fig.15 Average wind pressure coefficient curve

图16 平均风压系数分区图Fig.16 The partition figure of Cp on the roof surface
5 结论
本文研究了不同参数对四种典型双曲屋盖表面风压的影响规律,并总结分析出各屋盖的分区风压系数,主要得到如下结论:
(1)风向角对大跨度双曲屋盖表面风压分布存在较大影响;相对于风向角,地面粗糙度对屋盖的风压分布规律影响较小,且地貌对屋盖风压分布的影响主要体现在屋盖后方的出流处.随着地面粗糙度的增大,气流的再附作用越大.
(2)曲率比和矢跨比的变化对大跨度双曲屋盖风压系数的趋势影响较弱,其中屋盖中间区域的风压分布受曲率比和矢跨比的影响较大.随着曲率比减小,双曲屋盖表面风压系数受曲率比变化的影响增大;随着矢跨比增大,双曲屋盖表面风压系数受矢跨比变化的影响随之增大.
(3)相对于大跨度双曲屋盖的矢跨比,底座的高跨比对其表面风压分布的影响较小,但屋盖迎风前缘受到高跨比的影响很大,而屋盖的后半部分风压分布基本上不受高跨比影响.
(4)给出了方形和圆弧形双曲屋盖表面在最不利参数下的平均风压系数的分区建议值,为类似结构的抗风设计提供了有益参考.

