带有广义Beta 函数的积分型高阶Cauchy 中值定理

杜争光

（陇南师范高等专科学校 数学系，甘肃 陇南 742500）

近年来，积分型Cauchy 中值定理和高阶Cauchy 中值定理以及其“中间点”渐进性的研究取得了一些研究成果. 文献[1]对一类带有含参变量积分的Cauchy 中值定理做了讨论，给出了这类中值定理的一般形式；文献[2]讨论了带有积分上限函数的积分型Cauchy 中值定理，并对“中间点”的渐进性进行了研究；文献[3-4]对广义的高阶Cauchy 中值定理进行了讨论，对其“中间点”的渐进性进行了研究，得了“渐进性”的一个一般性的结论.

目前，将含参变量积分、积分上限函数和高阶导数结合起来的研究成果还不多. 为此，本文将讨论一类带有广义Beta 函数的积分型高阶Cauchy 中值定理，并讨论该类Cauchy 中值定理“中间点”的渐进性，以期对文献[5-9]中Cauchy 中值定理以及其“中间点”渐进性的研究成果进行补充和推广.

1 预备知识及主要引理

定义1设函数f∈ℝ[a,b]，对于∀t∈[a,b]，定义函数Lα,β（f）:[a,b]→ℝ为Lα,β（f(t)）=称Lα,β(f(t))是函数f(t)在区间[a,b]上的广义Beta积分或广义Beta函数.

对于定义1中的广义Beta积分，容易证明其有以下性质：

性质1当f(t)≡1时，对于∀α,β∈ℝ+，都有Lα,β（1）=B(α,β)(t-a)α+β-1.这里，B(α,β)=是Beta函数.

性质2若函数f∈ℂ[a,b]，且α＞1，则函数Lα，β(f(t))在闭区间[a,b]上可导，且有(α-1)La-1,β(f(t)).

性质3若函数f∈ℂ[a,b]，且α＞n(n∈ℕ)，则函数Lα,β(f(t))在区间[a,b]上存在n阶导数，且有

引理1设函数，若存在实数λ≥0，使得，则对于∀t∈[a,b]和∀α,β∈，以下极限成立：

证明由的定义，对于∀ε＞0，∃δ＞0，当0＜s-a＜δ时，有从而有（A-ε）(s-a)λ＜f(s)＜（A+ε）(s-a)λ，注意到(t-s)α-1(s-a)β-1＞0，所以，以下不等式成立：

对式（2）在区间[a,t]积分就有：

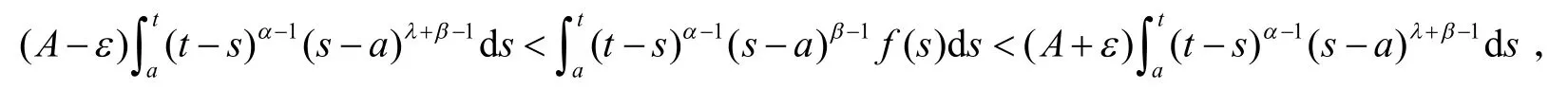
2 主要结论

2.1 高阶Cauchy 中值定理

定理1若函数f(s),g(s)∈ℂ[a,b]，且∀s∈(a,b)有g(s)≠0，则对于∀n,m∈ℕ和∀α,β,p,q∈[0,+∞)(α＞n,β＞m)，以及∀x∈[a,b]，至少存在一点ξ∈(a,x)，使得：

称式（3）是带有广义Beta 函数的积分型高阶Cauchy 中值定理. 这里，是Beta 函数.

证明对于∀n,m∈ℕ和∀α,β,p,q∈[0,+∞)(α＞n,β＞m)以及∀t∈[a,x]，考察以下函数：

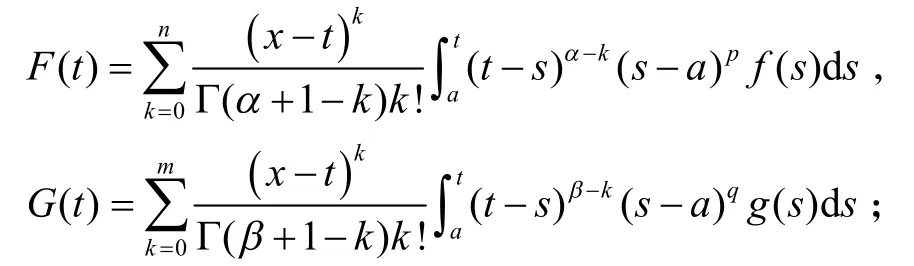
由函数F(t)和G(t)的构造，显然F(t)和G(t)在区间[a,x]上有以下等式成立：

由性质2和性质3，F(t)和G(t)在区间[a,x]上可导，且有：

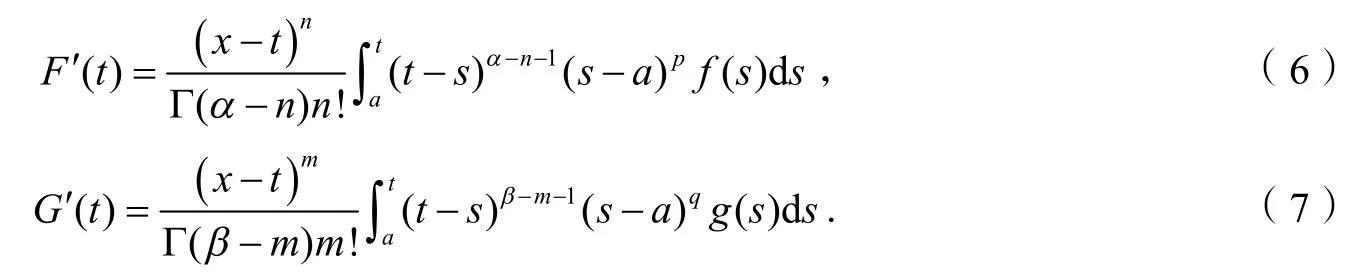
所以，函数F(t)和G(t)在区间[a,x]上满足Cauchy 中值定理的条件，由Cauchy 定理，至少存在一点ξ∈(a,x)，使得：

将式（4～7）代入式（8），就有：

整理上式，并注意到n!=Γ(n+1)和就有：

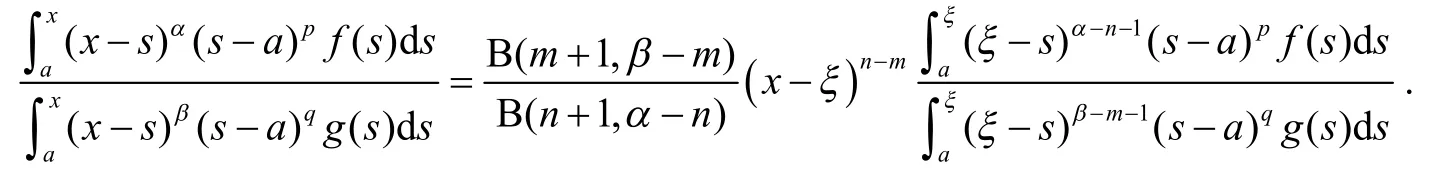
定理证毕.

推论1若函数f(s),g(s)∈ℂ[a,b]，且∀s∈(a,b)有g(s)≠0，则对于∀n,m∈ℕ和∀p,q∈[0,+∞)，以及∀x∈[a,b]，至少存在一点ξ∈(x,b)，使得：

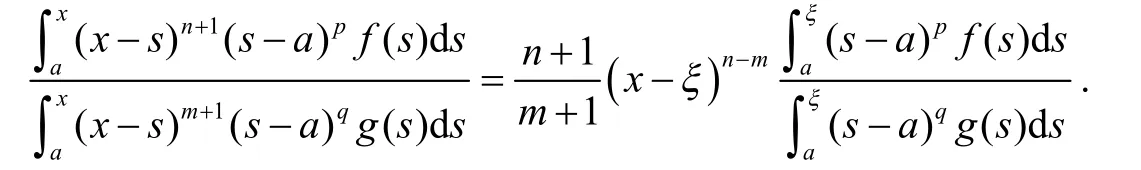
推论 2若函数f(s),g(s)∈ℂ[a,b]，且∀s∈(a,b)有g(s)≠0，则对于∀n,m∈ℕ和∀p,q∈[0,+∞)，以及∀x∈[a,b]，至少存在一点ξ∈(x,b)，使得：

证明辅助函数与定理1 相似，此时辅助函数应该为：

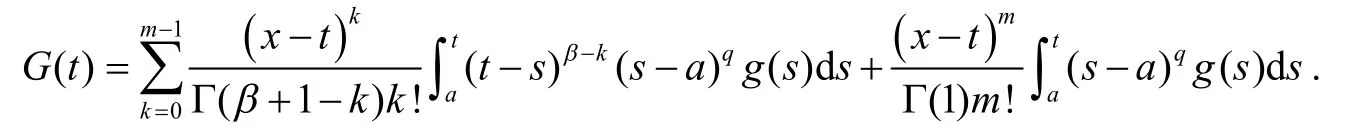
定理1 中的参数α、β、n 和m 选取不同的数值时，便有一系列推论，不再赘述.

2.2 中间点的渐进性

定理 2设函数f(s),g(s)∈ℂ[a,b]，且∀s∈(a,b)有g(s)≠0，若存在实数λ≥0和μ≥0，有和，则对于∀n,m∈ℕ和∀α,β,p,q∈[0,+∞)（α＞n,β＞m）以及∀x∈[a,b]，由定理1 确定的“中间点”ξ满足：

证明由于函数f(s)和g(s)在[a,b]上连续，对于∀α,β,p,q∈[0,+∞)，构造函数：H(x)=.则由引理1，

又由定理1，

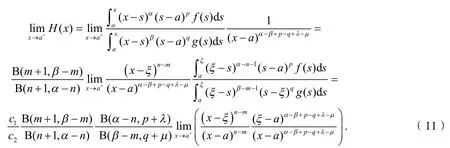
由式（10～11），得：

整理得：

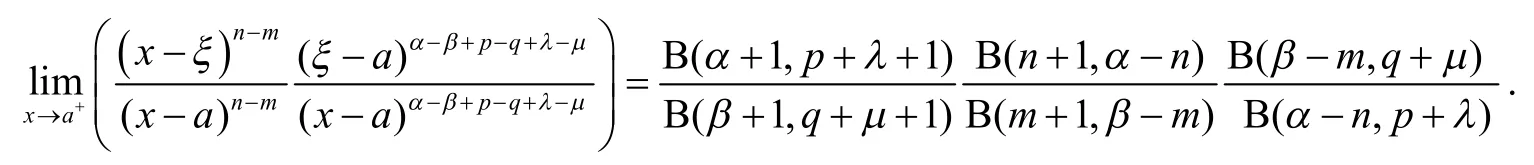
定理2 得证.

推论3设函数f(s),g(s)∈ℂ[a,b]，则对于∀n,m∈ℕ和∀p,q∈[0,+∞)以及∀x∈[a,b]，由推论1确定的“中间点”ξ满足：

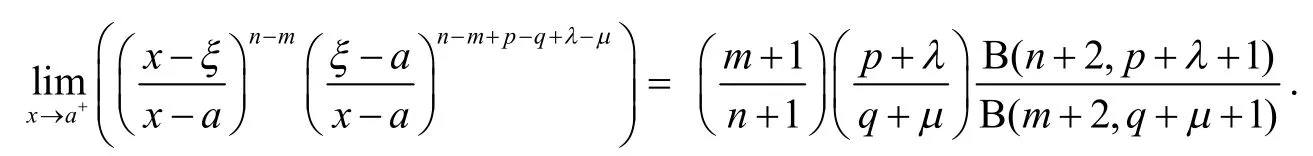
推论4若函数f(s),g(s)∈ℂ[a,b]，则对于∀n,m∈ℕ和∀p,q∈[0,+∞)以及∀x∈[a,b]，由推论2所确定的“中间点”ξ满足：

以上定理和推论的结论具有一般性，可作为Cauchy 中值定理“中间点”渐进性研究成果的补充和推广.