Fredholm型泛函积分方程基于Nystrm插值的两层网格解法

王奇生，周惠敏

（五邑大学 数学与计算科学学院，广东 江门 529020）

本文考虑一类Fredholm型泛函积分方程

其中f(x),α(x),k(x,t)为适当光滑的已知函数，u(x)为未知函数，且泛函因子α(x)满足如下的条件：

令y=α(t)，则

这样，将式（1）等价转化为在子区间上积分的Fredholm型积分方程（3），其中=±λ，或者[，

积分方程的数值解法主要有配置与谱配置方法[1-2]、最佳平方逼近与Galerkin投影逼近方法[3-4]、变分迭代与不动点迭代方法[5-6]、无网格与两网格方法[7-9]和小波与多尺度方法[10-12]等等. 但很少有文献研究泛函积分方程的两层网格解法，本文的研究丰富了Fredholm型泛函积分方程的高效数值方法.

1 解析解存在唯一性的充分条件

利用Banach不动点原理，给出方程（1）解析解存在唯一性的条件.

定理1（解析解的存在唯一性） 假设泛函因子满足条件（2），并且有

则积分方程（1）存在唯一解.

证明令T是C[a,b]到C[a,b]上的映射，有对任意的u1,u2∈C[a,b]有

2 粗网格上Nystrm插值解以及其收敛性

和

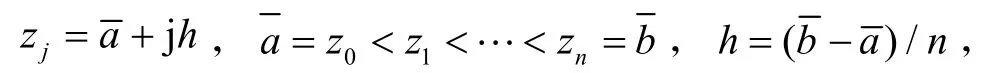
其中n＞m.

选择网格点为求积节点，分别在粗细两层网格构造高效数值求积公式

和

其中，求积系数与余项分别满足

令x=yi，并忽略余项得到粗网格上的离散化的线性方程组

等价的矩阵方程为

其中Gm=(gij)(m+1)×(m+1),Um=(um(y0),um(y1),…,um(ym))T,Fm=(f(y0),f(y1),…,f(ym))T，当i≠j时，gij=当i=j时，

利用式（4）和（7）可得

因此，系数矩阵Gm是严格对角占优矩阵，故

则

称为u(x)在粗网格节点上满足插值条件（12）的Nystrm插值函数，也叫Nystrm插值解. 下面给出粗网格上Nystrm插值解的收敛性结果.

定理2（Nystrm插值解的收敛性定理） 设u(x)为积分方程（3）的真解，um(x)为对应数值积分公式（5）下的Nystrm插值解，如果均满足上述条件（2）、（4）、（7），则成立如下的误差估计式：

证明由式（8）减去式（13）得

则

利用式（4）和（7）可得

整理得到

下面就数值积分公式分别选取复化梯形公式和复化辛普森公式，分别给出Nystrom插值解收敛性结果的两个推论.

推论1在定理2的条件下，如果数值积分为复化梯形公式，则

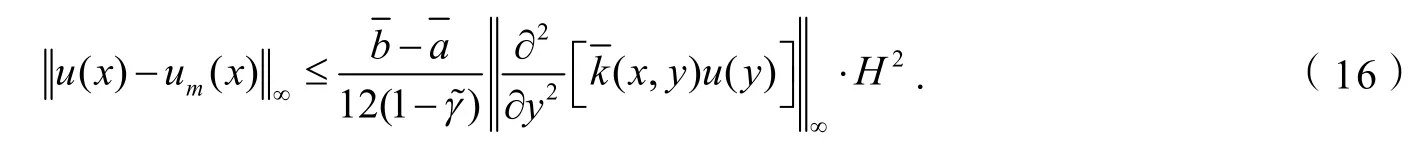
推论2在定理2的条件下，如果数值积分为复化辛普森公式，则

3 不动点迭代两网格解以及其收敛性

对于方程（3）的数值积分离散化，其计算复杂程度有赖于网格剖分的直径h，数值计算的工作量通常是O(n3)，这里n=1/h.因此构造合适的两层网格算法能较好地解决计算复杂性的困难.下面分三步介绍一种不动点迭代逼近方法，得到细网格上Nystrm插值解un(x)的逼近解，也称两网格解.

1）选取细网格解un(x)的初始迭代为粗网格解um(x)，即对任意亦即有初始值

2）对任意x∈[a,b]，在细网格上定义Nystrm插值解

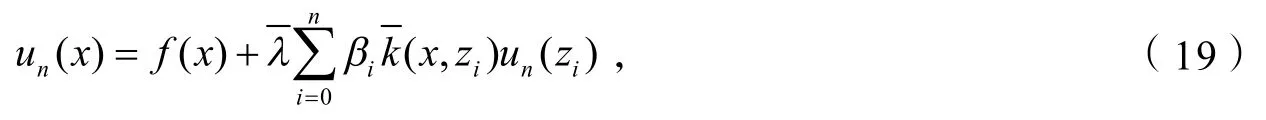
其中βi,zi（i=1,2,…,n）分别为细网格的求积系数和剖分节点.

3）对任意x∈[a,b]构造迭代格式

证明将式（19）和（20）两边相减得到

则

这样，逐步递推可得

利用式（4）和（7）可得

4 数值例子

本节给出了数值例子阐述上述理论分析的可行性及有效性. 考虑Fredholm型泛函积分方程

表1 复化梯形公式下计算结果

表1 复化梯形公式下计算结果

8 1.316 8e-05 5.327 7e-05 4.734 8e-04 16 3.291 9e-06 4.000 1 1.331 7e-05 4.000 7 1.183 7e-04 4.000 0 32 8.229 5e-07 4.000 1 3.329 2e-06 4.000 1 2.959 3e-05 3.999 9 64 2.057 4e-07 4.000 0 8.323 0e-07 4.000 0 7.398 2e-06 4.000 0

表2 复化辛普森公式下计算结果

表2 复化辛普森公式下计算结果

4 0 0 0 8 3.243 2e-20 0 0 0 0 0 16 7.141 5e-20 0.454 1 2.703 5e-19 0 0 0 32 1.034 6e-19 0.690 3 4.024 5e-19 0.671 8 0 0

其次将迭代解的收敛率定义为Ratio2=选取(m,n)分别为（8,32）（8,64），（16,64），对式（24）、（25）以及（26）分别计算它们的细网格解un(x)和迭代解之间的最大误差（见表3），其中3,4,5,6，数值积分采取复化梯形公式.最后针对（α1(x),f1(x)）的情况，给出当m=8，n=64，k=6时其真解u(x)、粗网格解um(x)以及迭代解的图像（见图4）.

图4 复化辛普森公式下（α1(x),f1(x)）解的图像

表3 复化梯形公式下计算结果

表3 复化梯形公式下计算结果

?