关于分块三角矩阵的几个行列式不等式
刘俊同
(阜阳师范大学 数学与统计学院,安徽 阜阳 236037)
AT,,A*分别表示矩阵A的转置,共轭以及共轭转置。对于两个n级厄尔米特矩阵A和B,若A-B是半正定矩阵(正定矩阵),则记作A≥B(A>B),因此,A≥0(A>0)表示A是半正定矩阵(正定矩阵)。用In表示n级单位矩阵,在不需要界定矩阵的级数时常用I来表示单位矩阵。对于两个相同级数的矩阵A和B,用A°B表示矩阵A和B的Hadamard积,用来表示多个矩阵Ak(k=1,…,m)的Hadamard积。n级方阵A若满足A*A=AA*,则称A为正规矩阵[1]。

国内外有许多专家学者致力于研究半正定矩阵行列式不等式[3-12]。
任一半正定矩阵A都可分解成A=T*T,其中是一分块三角矩阵,且和A具有相同的分块方式,利用(1),很容易证明

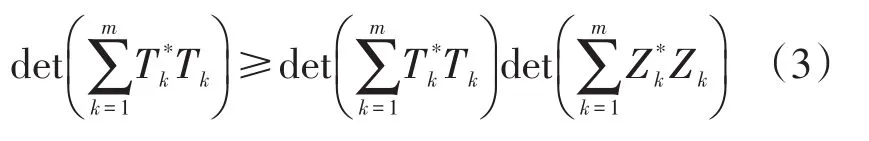
利用Fischer型反向不等式(3),Lin在文献[13]中还证明了


其中,Xk和Zk是正规矩阵。
Liu等在文献[14]中对Fischer型反向不等式(3)给出了如下模拟,即涉及 Hadamard积的Fischer型反向不等式
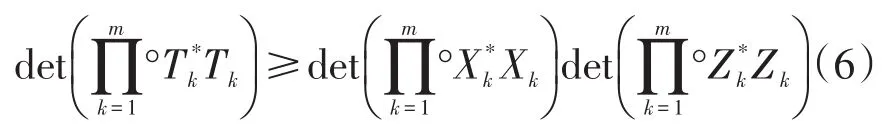
利用Fischer型反向行列式不等式(6),再结合Hadamard积和复合矩阵的若干性质[15],本文旨对不等式(4)和(5)给出关于Hadamard积的模拟,即涉及Hadamard积的行列式不等式。
1 辅助引理
为证明主要结果,先给出几个引理。其中引理1是Hadamard积的简单性质,引理2和引理3是矩阵论的基本结果,引理4是复合矩阵的一个简单性质[2,15]。
引理1设A是n阶级正定矩阵,B是n级半正定矩阵,则有

且(7)式中的等式成立当且仅当Y=0。
证明设矩阵A和B的对角元分别为ai,bi,i=1,…,n即
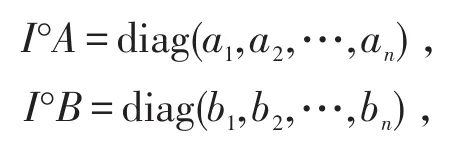
因为A正定,B半正定,于是有ai>0,bi≥0,i=1,…,n且有
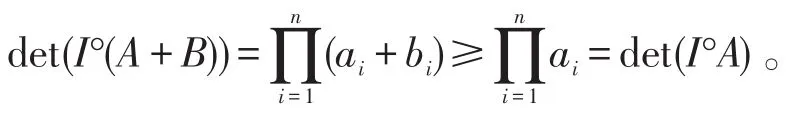
于是(7)式成立,并且由上述不等式知(7)式中的的等式成立当且仅当bi=0,i=1,…,n,再结合矩阵B的半正定性,因此有(7)式中的的等式成立当且仅当Y=0。
引理2设A是n级矩阵,则有A*A=0当且仅当A=0。
引理3设A和B是两个n级矩阵,若A≥0且B≥0,则有A°B≥0[15]。
引理4设A,B,C,D均为n级方阵,若二分块矩阵,则有
2 主要结果及证明
定理1设是一n级分块三角矩阵,X和Z分别是r级和n-r级方阵,则有
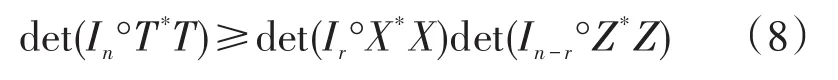
进一步地,若X和Z是非奇异的,则在(8)式中的等式成立当且仅当Y=0。
证明显然,不等式(8)是不等式(6)的特例,只需证明等式情形即可。若Y=0,显然有不等式(8)是一个恒等式。反之,由于
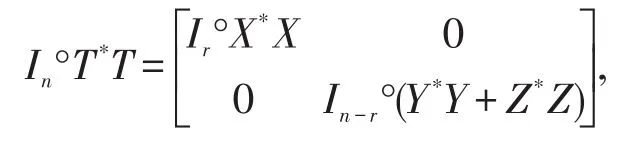
因此,有
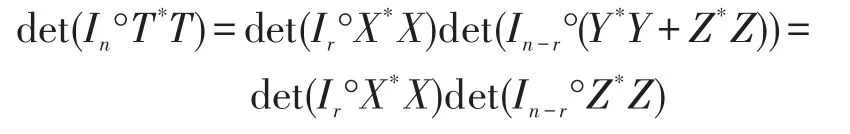
因为X是非奇异的,于是 det(Ir°X*X)>0 ,因此,有
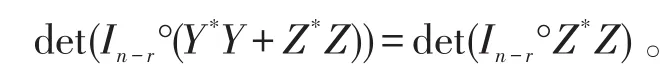
再由Z是非奇异的,于是Z*Z是正定的,Y*Y是半正定的,利用引理1和引理2易证(8)中的等式成立当且仅当Y=0。
注不等式(8)是不等式(4)关于Hadamard积的模拟。
定理2设是一组具有相同分块方式的n级分块三角矩阵,若Xk和Zk是正规矩阵,则有

证明考虑到Fischer型反向行列式不等式(6),要证明不等式(9),只需证明下述不等式
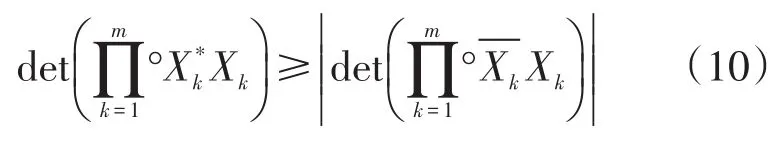
因为
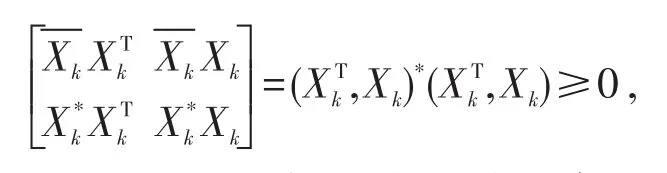
这里k=1,…,m,对指标k从1到m求Hadamard积,有

进一步地,有

等价地,有
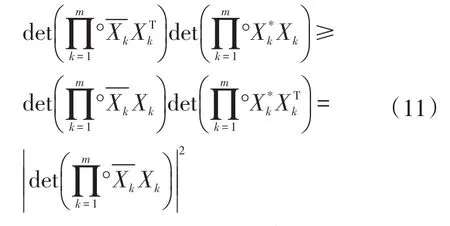
因为Xk,k=1,…,m是正规矩阵,所以
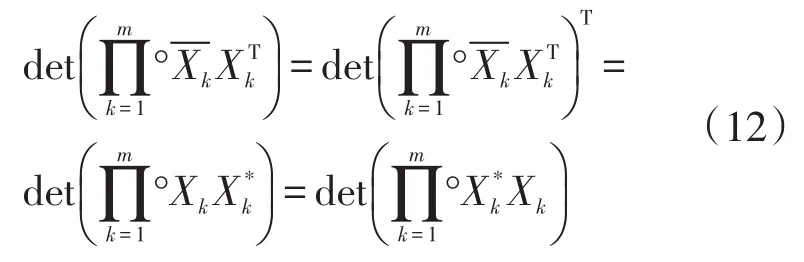
结合不等式(11)和等式(12),不等式(10)得证。
注不等式(9)是不等式(5)关于Hadamard积的模拟。
3 小结
Lin研究了分块上三角矩阵,得到了几个有趣的行列式不等式。对于Lin的部分结果,本文利用Hadamard积和复合矩阵的若干性质,证明了这些不等式关于Hadamard积的模拟不等式,即涉及Hadamard积的行列式不等式。

