基于卫星通信系统的单音干扰最佳干扰性能研究*

施白雪，徐 慨，蔡城鑫

（海军工程大学 电子工程学院，湖北 武汉 430000）

0 引 言

卫星通信具有通信距离远、覆盖范围广的特点，是主要的军用通信手段之一。因此，针对卫星通信的干扰技术研究具有重要的军事意义。MPSK是多元相移键控M-ary Phase Shift Keying的缩写，其中BPSK和QPSK被广泛应用于卫星通信。

此前已有诸多学者对单音干扰下的BPSK和QPSK数字调制信号误码率及其最佳干扰策略进行了研究[1-10]，但依旧存在两个问题：（1）研究基本都是基于干扰信号与通信信号载频一致的情况，而实际应用中，客观条件限制下，频率偏移必然存在且会对干扰效果产生影响；（2）在前人的研究中，相位的影响基本通过积分求均值排除，但从干扰方的角度，干扰平均效果没有意义，必须调整干扰功率，使干扰效果最差的相位干扰依旧有效，才能在实施干扰过程中无需考虑相位影响。本文针对QPSK调制进行严格的数学公式推导和仿真，研究单音干扰性能与频偏以及相位差的关系，得出QPSK调制下单音干扰的最佳干扰策略，并提出进一步的研究方向。

1 单音干扰性能分析

单音干扰（Single Tone Jamming，STJ）通常是指只具有一个频点的音频干扰，数学模型为：

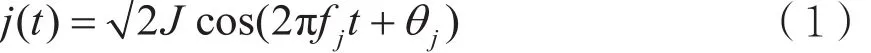
其中：J是音调的平均功率，ωj是它的频率，θj是它与目标信号的相位偏移。

单音干扰的时域图形与功率谱如图1所示。由于单音干扰仅作用于某个频点（实际上是带宽极窄的一小段频段），所以无法有效干扰跳频系统。但是，因其干扰功率集中的特点，对窄带信号的干扰有很大的优势，而常规卫星通信系统就是典型的定频窄带通信系统。

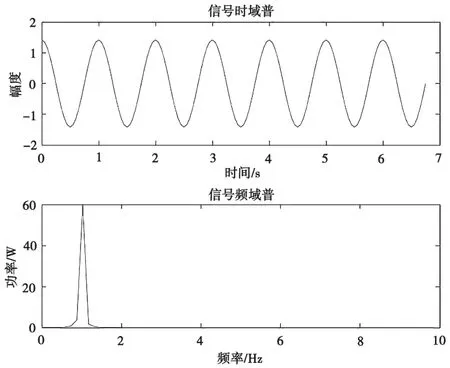
图1 单音干扰的时域图及功率谱

单音干扰的干扰效果按音调放置位置不同分为两种情况：

（1）干扰信号的频率与目标信号的载波频率相同，进行指向性干扰；

（2）干扰信号的频率偏离目标信号的载波频率，存在频率差Δω（本文不考虑由于滤波器特性对干扰性能的影响，即干扰信号远离滤波带宽边缘）。

为确保干扰效果，需要讨论相位对误码率的影响，尤其是在干扰阈值附近，相同条件下，相位有可能成为决定干扰是否有效的关键因素。

2 单音干扰对QPSK的干扰性能

QPSK调制模型如图2所示，数字信号在一个码元持续时间内经过QPSK调制后输出信号为：

图2 QPSK调制模型

QPSK可以被认为是两个BPSK调制器并行工作，将Q、I信道信号分别做相干解调，即可得QPSK解调结果，其相干解调程序框图如图3所示。

图3 QPSK相干解调

Q、I信道的载波正交，因此QPSK误码率与Q、I信道误码率关系如下：

由文献[10]可知，在没有单音干扰和编码下的QPSK的理论误比特性与BPSK系统完全相同[11]：

其中：Q(x)是马氏Q函数，也就是高斯随机变量超过均值x倍标准差的概率；Eb是每个信息比特的能量；N0是单边噪声谱密度。

当同时存在干扰信号和噪声时，解调接收机总输入信号为：

其中，单音干扰表示为：

式中Aj=2J为单音干扰幅值，J为单音干扰信号功率。单音干扰能够同时对Q、I信道信号进行干扰，干扰效果与单音信号和载波信号之间的频偏和相位差有关，且同一单音干扰信号对Q、I路信号的干扰效果略有不同，下面进行理论推导。

2.1 I路误码率计算

当干扰为连续单音信号和噪声（即对传号码元和空号码元同时进行干扰）时，相干解调器接收信号为：

其中，单音干扰载波相位θj是[0,2π]内均匀分布的随机变量；ωj=ω0+Δω，Δω为干扰信号与目标信号的频偏；n(t)为窄带高斯噪声，其均值为0、方差（平均功率）为Nt。

在发送“1”和“0”时，积分器的输出分别为：

式中nc1(t)和nc0(t)是噪声的同相分量，其均值为0、方差为N1N0，仍然是窄带高斯噪声。因此，积分器输出信号均值为：

方差为：

式中，n10和n00为nc1(t)、nc0(t)的单边带功率谱度函数为：

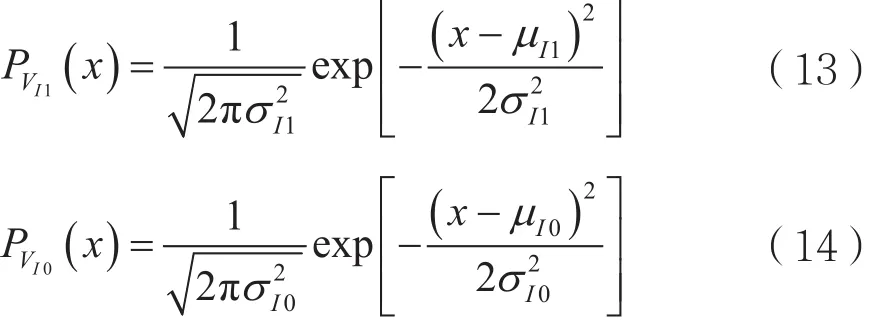
发送“1”错误接收概率为：

同理，可得发送信号“0”时的错误接收概率为：

“0”“1”等概率发送时，I路的总误码率为：

式中，B为积分带宽且TB≈1，令：

2.2 Q路误码率计算

如图3所示，QPSK的Q路信号解调过程与I路相似，推导过程同I路误码率，令：

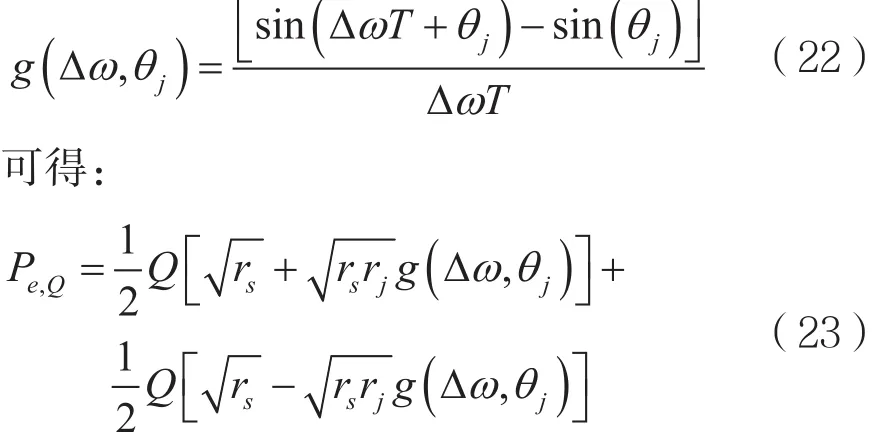
由式（21）和式（23）得QPSK误码率为：

此外，当干扰信号与目标信号不存在频差即Δω=0时，是一个特殊值，不能直接带入式（24）计算。按上述推导过程计算得：

3 仿真

卫星通信当前主要的业务有话音、数据、视频等，本文针对话音以及视频进行干扰效果评估。根据国际电信联盟（International Telecommunication Union，ITU）2008年公ITU-R.830-4建议书标准：Pe=10-4时，可以保证语音通信的可懂性；Pe=10-5时，可以保证视频通信可通。本文以卫星通信系统视频业务为例，取误码门限为[PE]th=10-5。

运用MATLAB软件对上述模型进行仿真[12-17]，卫星通信QPSK信号中频取70 MHz，初始相位为0，码元速率为2 Mb/s。假设不采用滚降滤波器，对以下3种情况进行仿真。

3.1 不存在单音干扰时

不存在单音干扰时的误码率曲线如图4所示。信噪比小于8.3 dB时，话音通信不可懂；信噪比小于9.5 dB时，视频通信不可通。为了确保在雨天及其他电磁环境下卫星通信系统仍能正常通信，设计系统时会留一定的链路余量。因此，正常工作时，卫星通信信号接收端的信噪比一般在10～20 dB。

3.2 存在同频的连续单音干扰

相位差范围为[-π,π]。由式（26）可知，相位差对误码率的影响在nπ/4内存在对称关系。因此，对[0,π/4]进行仿真，取rs=15 dB，结果如图5所示。

图4 仅存在热噪声的误码率曲线

对能够保障卫星通信的临界误码率Pe=10-5附近进行放大，结果如图6所示。

可以看出，在同频干扰的情况下，相位差对误码率存在一定影响。相位差扰效果最佳，即与Q路或I路同向时干扰效果最佳，能在更低的干信比下达到相同的干扰效果；时，干扰效果最差。最佳和最差的情况下，达到有效干扰时（Pe=10-4和Pe=10-5），干信比要求均相差2 dB左右。

图5 同频单音干扰的误码率曲线

图6 同频单音干扰的误码率曲线阈值放大后的结果

图7 同频单音干扰π/4相位差时误曲线

图8 同频单音干扰π/4相位差时误码率曲线放大后的结果

由此可得，当干信比小于-30 dB时，干扰无效，通信质量由噪声决定；之后随着干信比的增加，开始逐渐对误码率产生影响；在干扰阈值附近，环境噪声的影响比干扰噪声大，环境噪声改善1 dB时，需要大于1 dB的干信比改进才能达到一样的效果。

取rs=15 dB，rj=[-9 -5]误码率随相位的变化如图9所示。当rj=-9时，对于视频通信而言，相位差可能决定干扰是否有效；当rj=-7，相位差决定语音信号的可懂性。因此，在进行干扰时，务必要确保在干扰效果最差的情况下干扰有效。

图9 同频干扰时相位差与误码率关系曲线

3.3 干扰信号与目标信号存在频偏

以视频通信为例，取rs=15 dB，rj=10 dB，误码率与频偏、干扰初始相位关系三维图如图10所示。X-Z、Y-Z视角图分别如图11和图12所示。

不难看出，在同一频偏时，干扰信号的初始相位不同，误码率存在 0.6×10-5～1.1×10-5的误差；初始相位相同时，频率的偏移也会带来0.3×10-5～1×10-5的误差。在rs=15 dB，rJ=-10 dB的情况下，频率的偏移以及初始相位的选择，都可能影响干扰是否有效。

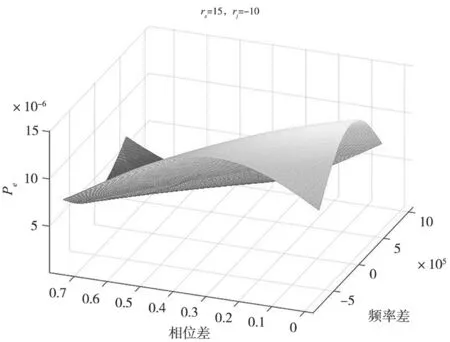
图10 单音干扰频谱、相位差与误码率关系三维图

图11 相位差-误码率关系视角图

图12 频谱-误码率关系视角图

三维图形能够客观观察整体的变化情况，但关于某一变量的变化规律观察较为困难。取特定的初始相位得到以下二维图形进行分析和讨论。当rs=15 dB，rJ=-10、-9、-8 dB，误码率与频偏以及干扰信号初始相位关系如图13、图14和图15所示。

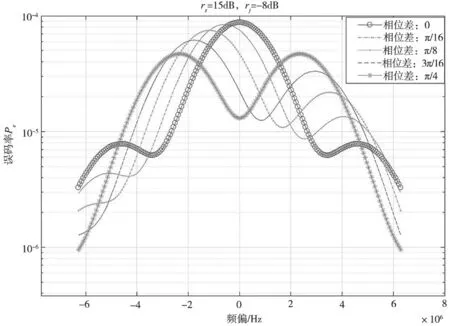
图13 rs=15，rj=-10时频偏与误码率关系

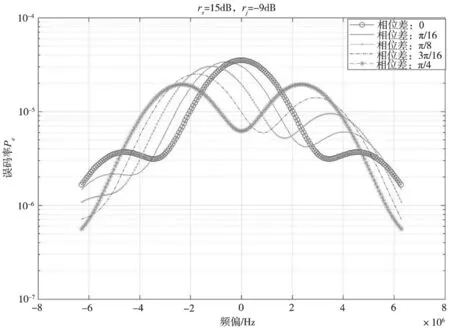
图14 rs=15，rj=-9时频偏与误码率关系

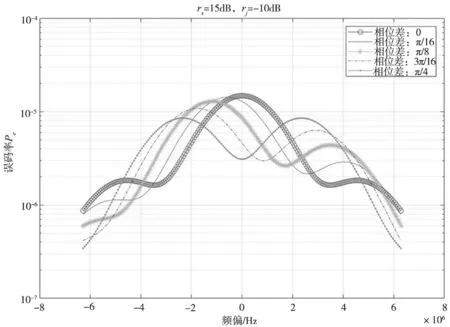
图15 rs=15，rj=-8时频偏与误码率关系

可以看出，只有在相位差为0的情况下，同频的单音干扰的干扰效果最好，且频率偏移对误码率的影响比相位差的影响要大。实际干扰中很难消除干扰信号与目标信号之间的相位差，因此往往是有一定的频率偏移时比同频干扰的效果会更好。

对实际情况下的单音干扰进行仿真（即同时存在相位差和频偏），干信比rj与误码率Pe关系如图16～图19所示。可以清晰看到，当相位差不为0时，频率进行适当偏移，达到相同的干扰效果时（相同Pe），信噪比要求反而更低，与以上结论一致。

图16 相位差π/16时不同频偏下干信比与误码率关系

图17 相位差π/8时不同频偏下干信比与误码率关系

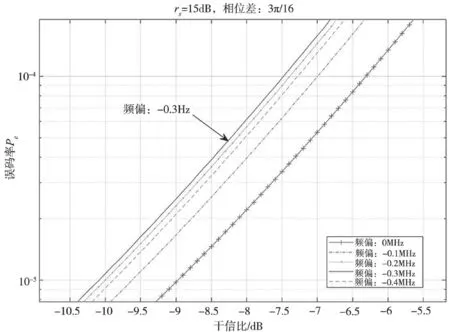
图18 相位差3π/16时不同频偏下干信比与误码率关系

图19 相位差π/8时不同频偏下干信比与误码率关系

4 结 语

本文对QPSK调制通过公式推导和Matlab仿真得出单音干扰对数字通信的最佳干扰，尤其是在干扰与目标信号同时存在频率偏移时，干扰信号的频偏以及相位差对干扰效果的影响，得到了单音干扰对QPSK调制解调系统进行干扰时的两个重要结论：（1）当进行指向性干扰即干扰信号与载波信号频为干扰阈值；（2）当无法消除相位的影响时，干扰信号存在一定频偏时的干扰效果比指向性干扰的干扰效果理想。这两个结论在实际应用中，对干扰方如何确保干扰的有效性具有重要意义。

本文仅针对QPSK进行了大量的数学推导和Matlab仿真，对进行整个卫星系统的仿真是下一步研究的方向，并进行系统化的仿真，通过在实际情况下的实验结果验证推导结果。最后，在无法精确瞄准目标信号频率的时候给定误差范围，能否找出干扰效果的阈值，也是下一步研究的重点。