临床用血需求的ARIMA模型预测

彭荣荣，刘芸男，杨冬燕，王含柔，赵明烽，杨小丽

1)重庆医科大学公共卫生与管理学院；医学与社会发展研究中心；健康领域社会风险预测治理协同创新中心 重庆 400016 2)重庆市血液中心 重庆 400015

自《献血法》颁布实施以来，我国已建立起横向到边、纵向到底、覆盖城乡的采供血服务体系，形成了以血液中心为龙头、中心血站为基础、中心血库为补充的三级服务网络，血液供应能力、临床合理用血能力以及血液安全水平显著提高。根据世界卫生组织研究报告，当无偿献血率达1%～3%时才能满足该国基本的用血需求，2017年我国无偿献血率为1.05%，总体上看，我国血液保障能力尚处于“紧平衡”状态[1]。近些年随着地市级医疗机构服务能力的提高和医院规模的不断扩张，以前不得不去省级综合型医疗机构就医的患者选择到中心血站覆盖的地市级医疗机构接受治疗，造成地市级医疗机构血液用量迅速增长，中心血站血液供应面临巨大压力和挑战，血液供应紧张的现象已呈现常态化趋势，区域性、季节性和结构性缺血现象时有发生[2]。据报道，2014～2016年，重庆市中心血站供血量增长5%，而同期床位数、住院人次数及手术人次数均以两位数增长，其中手术人次数的增长是血液供应量增长的3倍[3]。如何科学地预测临床用血需求，确保血液供给与需求之间的平衡值得深入研究。目前对临床用血需求的预测主要是依据相关人员既往经验进行粗略估计。自回归移动平均模型(autoregressive integrated moving average model，ARIMA)是一种时间序列模型，描述时间序列数据的变化规律和行为，可用于包含趋势变动、季节变动等不同特征的时间序列建模并进行预测。本研究拟采用时间序列分析方法探究临床用血历史数据随时间发展变化的规律，通过建立ARIMA模型预测临床用血需求，为中心血站科学制定招募及采集计划提供依据。

1 资料与方法

1.1数据来源收集2006年1月～2016年12月重庆市万州中心血站每月向医院提供的悬浮红细胞的原始数据。临床用血量以U为单位计算，1 U悬浮红细胞由200 mL全血分离制备。

1.2ARIMA模型的建立①时间序列情况分析及序列平稳化处理：根据原始序列图判断该序列是否平稳，若不平稳，则需对序列的趋势和季节性趋势进行差分和季节差分处理使其平稳。②模型识别：绘制平稳序列的ACF和PACF图，判断其拖尾或截尾情况以便为目标模型定阶，并选定1～2个模型作为备选模型。③模型参数估计与检验：对备选模型进行参数估计与假设检验，并依据BIC准则确定最佳模型。然后对模型的残差序列进行白噪声诊断，根据残差序列ACF和PACF是否落在95%CI内，或Ljung-Box统计量有无统计学意义进行判定。④模型预测：运用选定模型预测需求值，计算95%CI以及相对误差，并与同期实际值比较，以验证模型的拟合效果。

1.3统计学处理运用Excel建立数据库，采用SPSS 19.0进行数据统计分析。其中2006年1月～2016年6月的悬浮红细胞临床用量原始数据用于模型建立，2016年7月～2016年12月的原始数据用于验证模型的预测效果。

2 结果

2.1时间序列分析及平稳化处理有鉴于原始序列存在明显的趋势性和季节性，故选用ARIMA乘积季节性模型，即ARIMA(p,d,q)(P,D,Q)s。序列的季节周期为12个月，故S=12；因进行了一阶差分和一阶季节差分，故d=1，D=1。绘制2006年1月～2016年6月每月悬浮红细胞临床用量原始序列图(图1上)，可见2006～2011年临床红细胞用量逐年上升，2012～2016年逐渐变缓；同时该序列还存在明显的季节周期性，以12个月为一个周期，每年的7～8月是供血高峰，1～2月则是低谷。经过一阶差分和一阶季节差分后序列中每个值都围绕在固定值附近波动，为平稳序列(图1下)。

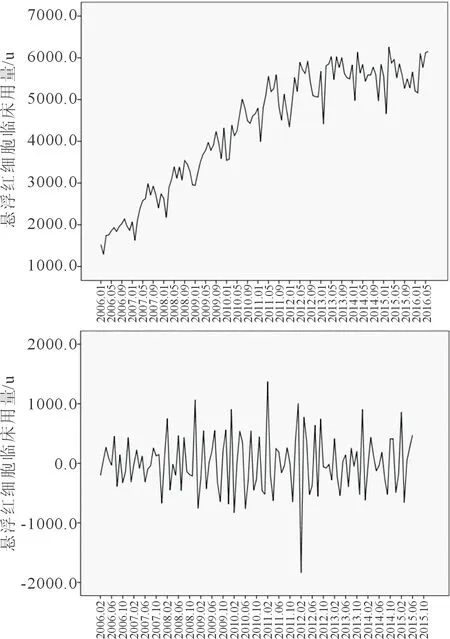
图1 原始(上)、一阶差分和一阶季节差分后(下)的序列图

2.2模型识别绘制ACF和PACF图(图2)，可见PACF第1～3期特别突出，第4期后明显收缩，判断PACF呈3阶截尾，故p取3；ACF第1、3、5、10、13期都有突出，因此判断ACF拖尾或者截尾特征不明显，故q取0；同时，ACF在12阶显著不为0，故q=1；PACF在12阶附近显著不为0，故p=0或1。由此获得2个备选模型，即ARIMA(3,1,0)(0,1,1)12和ARIMA(3,1,0)(1,1,1)12。

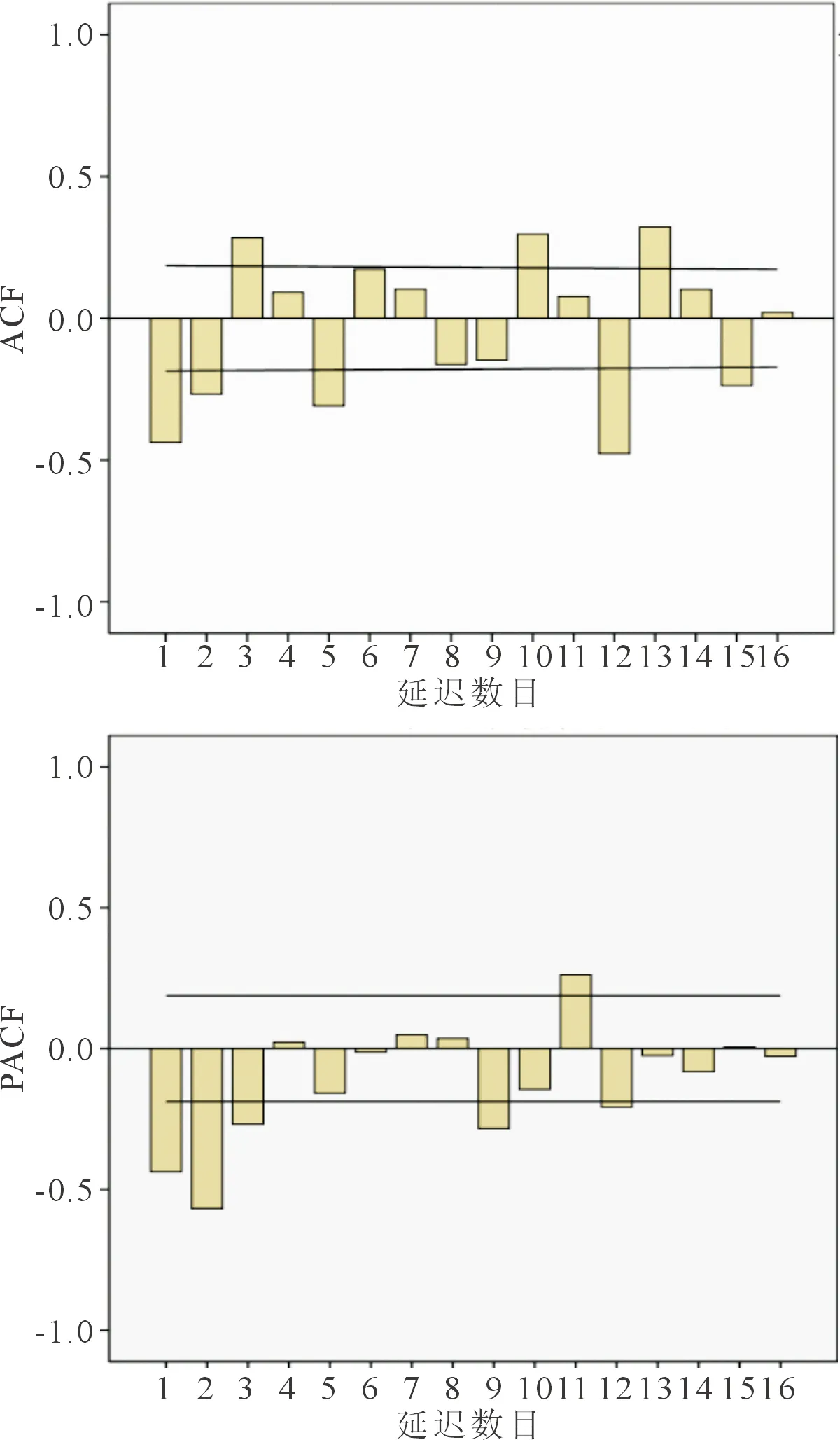
图2 一阶差分和一阶季节差分后的ACF和PACF图

2.3模型参数估计与检验2个备选模型的参数估计及假设检验结果见表1。根据贝叶斯判定准则[4]，模型ARIMA(3,1,0)(0,1,1)12的BIC值小于模型ARIMA(3,1,0)(1,1,1)12，故最终选择模型ARIMA(3,1,0)(0,1,1)12。

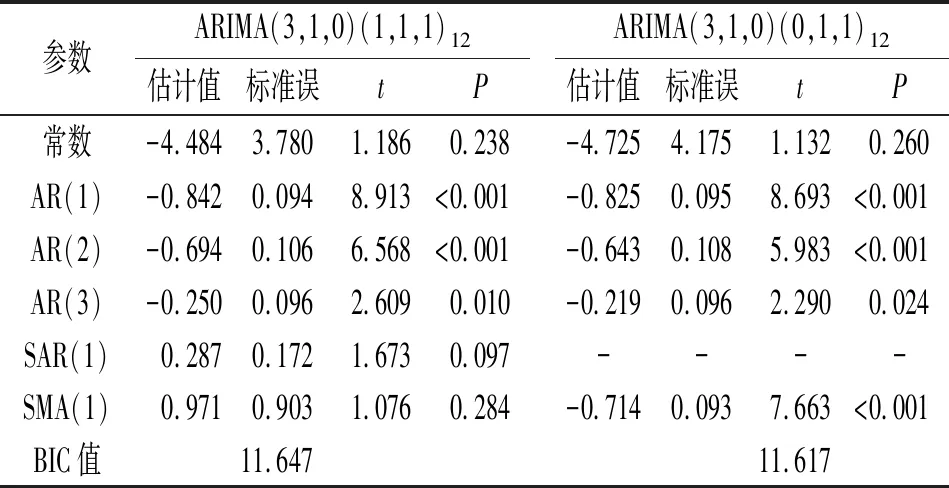
表1 2个备选模型的参数估计及假设检验

对模型ARIMA(3,1,0)(0,1,1)12的残差序列进行白噪声诊断，结果见图3。残差序列ACF和PACF落在95%CI内；Ljung-Box统计量无统计学意义(P>0.05)，说明残差是随机分布的，模型充分提取了原序列中的数据信息，适用于临床悬浮红细胞需求量的预测。

图3 ARIMA(3,1,0)(0,1,1)12残差序列ACF和PACF图

2.4模型预测应用ARIMA(3,1,0)(0,1,1)12模型对2016年7～12月每月的悬浮红细胞临床用量进行预测，并将预测值与同期实际值进行比较，平均相对误差为4.27%(表2)，模型拟合图中预测值与实际值的趋势相同(图4)。平均相对误差小于5%说明模型的预测结果精度较高，预测拟合效果好[5-7]。

表2 2016年7～12月份悬浮红细胞临床用量预测值与实际值的比较

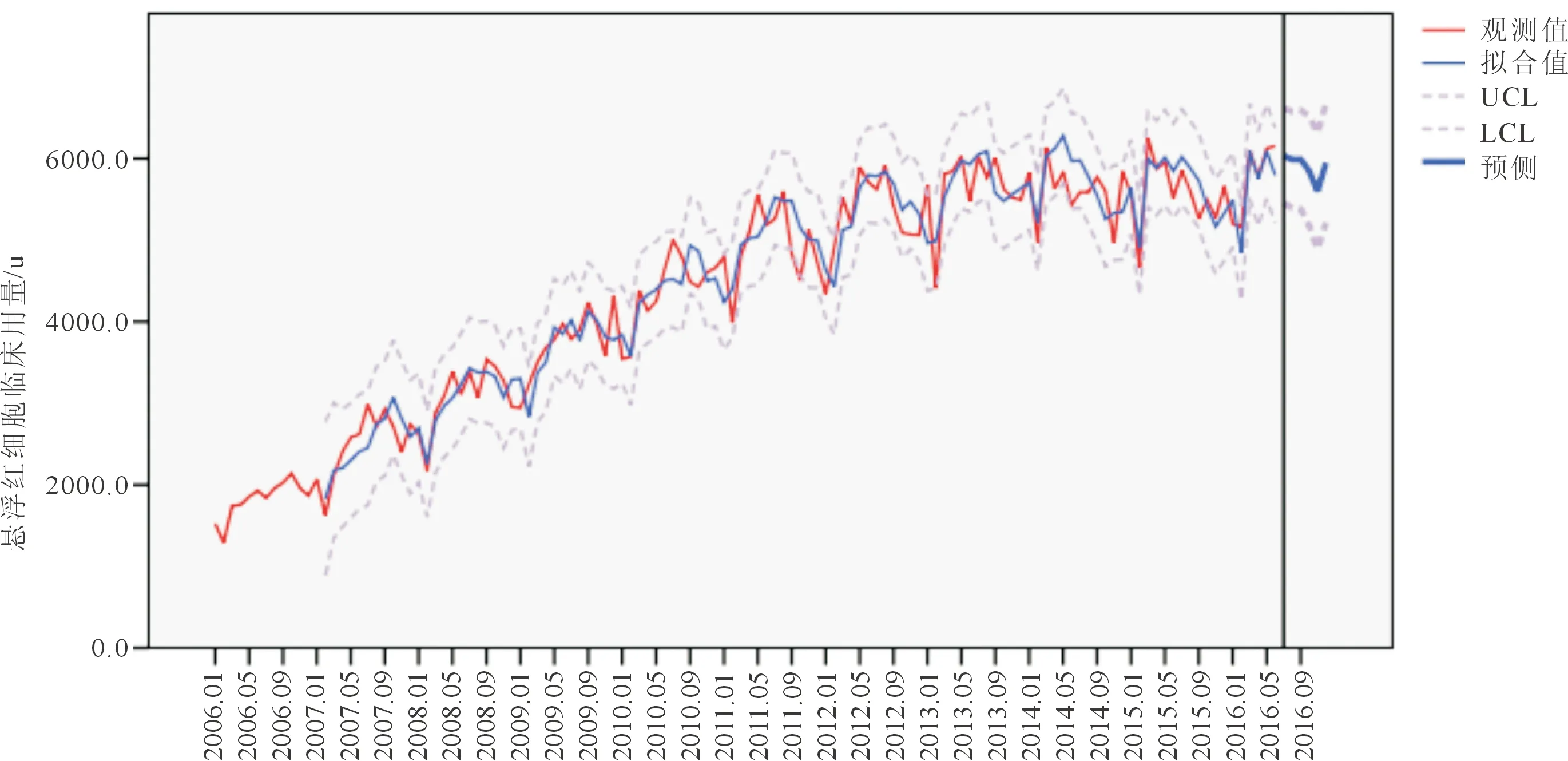
图4 悬浮红细胞临床用量ARIMA(3,1,0)(0,1,1)12模型拟合效果图

3 讨论

时间序列是指对于随时间变化的某种现象，根据时间间隔顺序记录下的一列有序数据；时间序列分析是探究包含在这组按时间间隔顺序记录下的真实数据中的所有信息，研究其在长期变动过程中所存在的统计规律性，并通过建立统计模型实现预测和控制将来事件的目的[8]。时间序列分析方法主要有两大功能：一是描述功能，通过建立模型来描述某种现象随时间推移的变化规律；二是预测功能，利用某现象过去和现在的数据资料预测将来事件[9]。ARIMA模型是时间序列分析中最重要和常用的方法之一，它针对随时间变动的序列建模，对每个季节周期中同时间点的序列值进行分析，提取季节趋势，并对每个季节周期内部序列值的变化提取非季节性成分来做预测[10]。近年来ARIMA模型在医疗卫生领域中的应用已较为广泛，主要集中于发病趋势的预测[11-13]，如梅毒发病率预测、乙肝发病数预测等。有文献[14]报道，ARIMA模型在预测医院临床血液需求量方面优于其他时间序列模型。

悬浮红细胞是一种红细胞成分血，是将采集的全血中绝大部分的血浆分离之后，向剩余的部分加入红细胞添加液而制成，它有减少输血不良反应发生、增强运氧能力等优点，但保存期限较短(低于35 d)。本研究将近些年血液供需矛盾较为突出的中心血站纳入研究视野，以重庆市采供血量最大的中心血站万州中心血站为研究对象，利用该血站2006年1月～2016年6月每月悬浮红细胞临床用量建立ARIMA模型，经模型识别、参数估计与检验，得出ARIMA(3,1,0)(0,1,1)12模型为最优模型；然后，运用该模型对万州中心血站2016年7～12月每月悬浮红细胞临床用量进行预测，结果显示预测值均在95%CI内，且预测值和实际值的动态趋势基本一致，平均相对误差较小(4.27%)，说明该模型的预测精度较高，可以用于该中心血站未来悬浮红细胞临床用量的预测。

建立悬浮红细胞临床用量数学模型，不仅有助于血站科学地制定招募采血计划，为加大团体献血的宣传力度、构建稳固的献血队伍、提高血液供给及需求之间的契合度提供科学的依据；同时也能帮助医院在模型预测的、采供血机构可以提供的悬浮红细胞用量的基础上，科学合理地进行输血治疗和手术安排，这对指导临床工作具有极其重要的作用。然而，ARIMA模型也具有一定的局限性，它是依靠历史数据建立的数学模型，是基于数据本身规律进行的预测，并未考虑国家重大政策改变和调整、突发事件等外部因素的影响[15]。因此，ARIMA模型仅适用于短期结果预测，在悬浮红细胞未来临床需求的预测中，预测时间不宜过长，以1 a较为恰当[16]。预测时间过长会增大预测误差，影响预测精度。近年来，健康中国战略的实施、二孩政策的推行、人口老龄化的加速等都促发了临床用血刚性需求的增长，尤其是2018年互助献血取消以后，临床用血的缺口加大，这些均可能对预测效果产生影响。因此，每年应及时更新悬浮红细胞临床用量信息，根据最新数据重新选定ARIMA模型，以确保预测的精度。