利用迭代加权模糊度函数法的单历元模糊度固定

高 迪，何文涛，蔺晓龙

(1. 中国科学院大学，北京 100049； 2. 中国科学院微电子研究所，北京 100029)

卫星定姿技术具有成本低、精度高、无累计误差等优势，广泛应用于汽车、船舶、航天器等的姿态测量中。为了快速持续地获取载体的精确姿态，整周模糊度需要快速精确地固定。模糊度固定方法可以分为3类：第一类是基于观测域的解算方法，代表方法为双频P码伪距法。第二类是基于模糊度域的解算方法，代表方法为最小二乘模糊度去相关算法(LAMBDA)。在LAMBDA的基础上，继而发展的带基线长度约束的最小二乘模糊度去相关算法(CLAMBDA)，进一步提高了模糊度固定的成功率[1]。但CLAMBDA的固定成功率依赖于浮点解的精度，没有解决在低精度浮点解情况下模糊度固定率降低的问题[2-4]。第三类方法是基于坐标域的解算方法，代表方法为模糊度函数法(ambiguity function method,AFM)[5]。相比于LAMBDA，其优势在于不需要浮点解，并且可以忽略周跳带来的影响，但其缺点是搜索空间巨大，计算量过大，无法满足实时性的要求。

近年来，随着微型惯性测量单元(MIMU)的发展，其精度不断提高，成本不断下降，利用MIMU辅助提高整周模糊度求解速度和成功率的算法不断被提出。文献[6—8]提出PCAFM算法，利用MIMU提供的俯仰角约束及基线长度约束对AFM算法的搜索空间进行压缩，满足了实时性需求。由于在复杂环境中，当发生多路径效应或测量噪声过大时，AFM算法可能会无法正确固定模糊度，因此文献[9]设计了基于MIMU的平滑模型对载波相位观测值噪声进行抑制。针对观测噪声的问题，文献[10]重新设计了模糊度函数法中的适应度函数，提出了能够对观测噪声自适应的滤波适应度函数。

上述基于AFM的优化算法都没有改进由于AFM算法忽略载波相位观测值整周部分带来的历史信息丢失而导致的性能易受到干扰的问题[11-12]。因此，在PCAFM的基础上，本文提出迭代加权模糊度函数法(iterative weighted AFM，IWAFM)，实现对载波相位测量值误差较大的卫星的抑制，在满足实时性的基础上，提升AFM算法在复杂环境中的模糊度固定成功率。

1 PCAFM算法简介

AFM算法的原理是在已知一个基准天线的地心地固坐标系(ECEF)的条件下，以基准天线为中心建立站心坐标系(ENU)，坐标系下模糊度函数值最大的点就是最佳匹配点[13]。双差载波相位观测值的模型定义为，b是天线间的基线矢量，pitch角用θ表示，yaw角用φ表示。两个天线可以同时接收卫星i和卫星j发播的信号，并获取卫星的坐标，ei和ej是在ENU坐标系下天线指向卫星的单位矢量。假设卫星i是进行双差的基准卫星。在短基线条件下，双差载波相位观测方程为

(1)

(2)

(3)

AFM算法的搜索过程可以用式(4)表示，根据文献[14]提出的适应度函数计算模糊度函数值

(4)

式(4)充分利用了双差模糊度的整数特性，借助余弦函数的周期性忽略了双差载波相位的整周部分，当估计值与观测值的小数部分完全匹配时，适应度函数取最大值。从上式可以发现，由于忽略整周部分，当观测噪声过大时，在搜索空间上可能有多个匹配度较高的峰值[15]。

2 迭代加权模糊度函数法

迭代加权模糊度函数法(IWAFM)在PCAFM的基础上，做出了两个较大改进，一个是设计了新的适应度函数，另一个是将迭代加权的思想引入到AFM算法中，通过迭代加权引入历史信息，一定程度上弥补了由于AFM算法忽略双差载波相位值整周部分而丢失的历史信息。

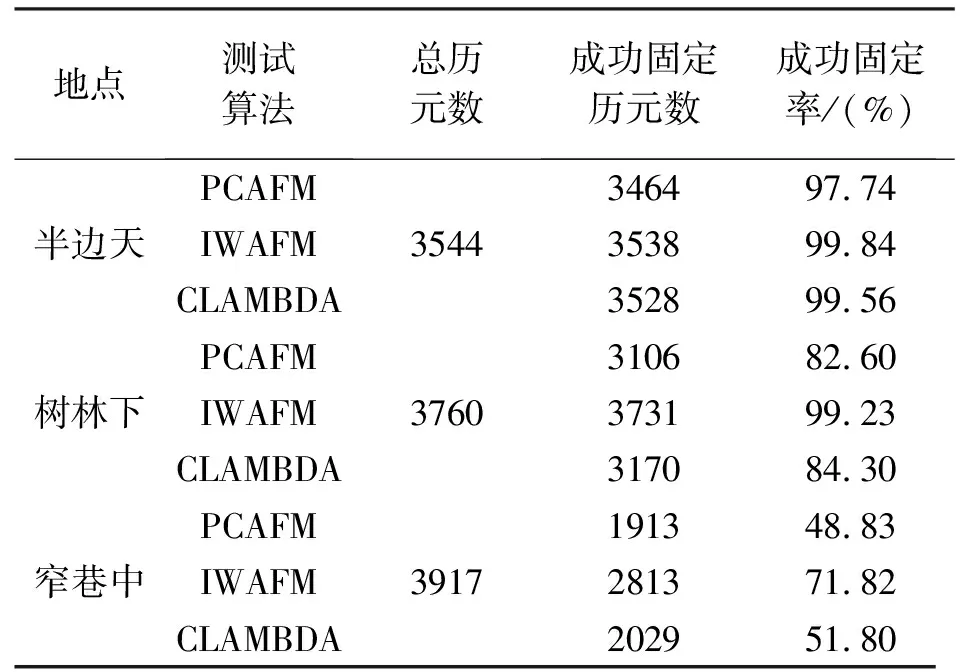
算法分为初始化阶段、迭代阶段。在算法初始化阶段，由传统的PCAFM进行搜索，重置所有卫星的置信值为相等，不更新置信值。设置一个亚阈值比例检验(ratiosub

2.1 适应度函数设计

经典的AFM算法中的适应度函数为余弦函数。当观测噪声较大时，遍历搜索空间得到的适应度函数值组成的曲面较为平滑，真值所在峰值不明显，与错误值的峰值难以区分。本文根据AFM算法只利用小数部分做匹配的特点，提出一种新的适应度函数，能够提高在不同坐标点上适应度函数值的区分度。

(5)

式中，利用round函数对双差载波观测值与双差载波估计值的差值进行四舍五入取整得到整周部分。在基准卫星为i的情况下，卫星j的双差残差定义为

(6)

在复杂环境中，由于多路径效应及测量噪声等的影响，在适应度函数值曲面除了真值以外的区域依然有许多峰值，对搜索真值带来很多干扰。使用了新的适应度函数后，相比于余弦函数，新的适应度函数值曲面的峰值更加陡峭，真值点的峰值更加突出。

2.2 迭代加权方法

(7)

(8)

式中,参数a和b，本文给出一组典型值，a=32.693 7，b=0.203 3。本文提出的置信值函数在迭代加权的过程中能够满足本算法对置信值函数的要求，并具有数值计算稳定性。将加权的过程融入适应度计算过程中。对rest代入到适应度函数计算时，每一项残差乘上相应的归一化权重为

(9)

2.3 权重正则化方法

算法实际测试过程中发现，如果对权重的计算不加以正则化，权重分布往往会陷入局部最优中。为避免少数卫星权重占比过大，本文给出一组正则化方法,包括抗积分饱和:根据选择的权重函数的数值特点，设定一个置信值积分上限值，当某一颗卫星的置信值触碰到积分上限时，所有卫星的置信值减半；限幅:当某一卫星的权重除以平均值大于某一阈值时，停止对它的继续累加；短时修复:每一颗卫星都有一个中断计数，在中断历元数的容忍度内的卫星置信值不重置。

3 试验结果及分析

在本文采用低成本的GNSS接收机和MIMU组成的组合导航系统中，GNSS接收机采用某公司的AT6558；采用MIMU的型号为博世BMA280。为验证IWAFM算法在复杂环境下的性能，试验地点为某大厦附近。在试验地点附近选择了3个典型城市环境地点：半边天、树林下、窄巷中。在静态试验条件下，GNSS接收机采用GPS+BDS单频双模模式，两个天线与GNSS接收机、MIMU放置在同一测量臂上，保存GNSS接收机和MIMU采集的数据，并对数据时间戳进行同步。对同一组数据分别运用PCAFM、IWAFM、CLAMBDA进行测试，算法中的模糊度确认步骤都采用比例校验法，ratio设置为3。试验结果见表1。

表1 3种算法计算结果

通过对试验结果进行统计分析，IWAFM算法相比于PCAFM和CLAMBDA算法能够在复杂环境下有效提升模糊度固定的成功率。在极端复杂环境下，IWAFM算法模糊度固定的成功率优于CLAMBDA算法。

图2展示了3种算法在树林下的航向角定向结果。通过图2(d)可以发现，在树林下的观测期间，卫星信号质量不佳，跟踪卫星数目变化频繁，接收机对卫星无法稳定保持锁定。同时在1000、2500和3000 s等附近，卫星数目变化剧烈的观测历元区间，PCAFM和CLAMBDA的算法性能下降，出现了很多无法模糊度固定的情况，但IWAFM在这期间，仍能保持稳定的性能。进一步分析3种算法最后固定的模糊度质量，根据IWAFM固定的模糊度最终计算出来的航向角波动更小，分布更为集中。

4 结 语

本文提出了一种利用MIMU信息辅助GNSS求解整周模糊度的迭代加权模糊度函数法。利用MIMU传感器系统给出的Pitch角缩小了搜索空间，极大地减少了IWAFM算法的计算量，使得该算法满足了实时性要求。定义了新的适应度函数，并引入迭代加权的思想，使得当GNSS接收机处在复杂环境中时，IWAFM算法能够对不同卫星的信号的权重进行自动调节。试验结果表明，IWAFM算法相比于PCAFM和CLAMBDA算法，能够在复杂环境中有效提高模糊度固定的成功率。未来的工作将在以下两个方面展开：①提升IWAFM算法在复杂环境中的精度和稳定性;②研究将利用双频信息进一步提升IWAFM算法的模糊度固定成功率。