利用GLAS激光测高数据评估DSM产品质量及精度优化

胡柳茹，唐新明，李国元，付冬暇，窦显辉，赵世湖

(1. 山东科技大学测绘科学与工程学院，山东 青岛 266590； 2. 自然资源部国土卫星遥感应用中心，北京 100048； 3. 自然资源部第一地形测量队，陕西 西安 710054)

激光雷达与成像光谱、合成孔径雷达一起被列为对地观测系统(earth observing system，EOS)计划最核心的信息获取技术[1]。美国发射于2003年搭载着GLAS(geosciences laser altimeter system)系统的冰、云和陆地高程测量卫星(ice cloud and land elevation satellite,ICESat)是资源三号02星之前唯一一颗对地观测的激光测高卫星[2]。星载LiDAR能够穿透云层、植被,具有高精度、全天时、覆盖广等特点,是全球高程控制点采集的有效方法[3-4]，是评估和验证数字表面模型(DSM)高程精度的重要手段，并为提高立体卫星无控测量高程精度提供可行性。文献[5]用公开地形数据、激光测距属性参数和回波波形特征参数的多准则约束筛选高程控制点，并利用高精度机载LiDAR成果数据验证筛选后的激光足印点的精度。文献[6—8]用ICESat建立了全球大地控制数据库，评估全球地形数据精度，并作为高程控制点以提高ASTER(advanced spaceborne thermal emission and reflection radiometer)GDEM(global digital elevation model)的高程精度。文献[9]初步验证了筛选后的GLAS激光点作为高程控制点提高资源三号立体卫星无控测量高程精度的可能性。

已有的研究主要是对高程控制点的筛选和对DSM的验证，较少讨论筛选后的高程控制点针对不同地形地貌的应用和DSM模型改正。本文针对星载激光测高技术在高程控制点的应用开展研究，以期拓展星载激光测高技术获取高精度高程控制点的应用。针对大范围、不同地形地貌的DSM进行精度验证和模型改正，提出境外DSM优化技术流程，为后续GF-7(高分七号)激光测高数据在DSM上的应用提供借鉴作用。

1 优化境外DSM技术的原理

由于境外地区外业像控点稀少，获取非常困难，因而缺乏有效的控制数据[10]。传统的境外DSM技术难以监测区域网平差的精度质量，对生成DSM的绝对高程精度缺乏有效的质量评估方法。激光测高可以快速、直接地获取地物三维空间信息，而且分辨率高、抗干扰能力强、低空探测性能好、穿透性强，是一种有效、快速地获取高程控制点的方法[11]。优化境外DSM技术的原理是利用激光测高数据作为高程控制点对DSM进行模型改正，有效提高无控测量高程精度，并对最终DSM进行质量评估。优化境外DEM技术流程如图1所示。

质量评估过程中对筛选后的GLAS点与DSM的高程求差ΔH=HGLAS-HDSM。DSM相对于高精度检查点的精度要求见表1。通过对ΔH进行统计分析，若ΔH的统计结果满足表1中DSM相对于高精度检查点的精度要求，则说明境外DSM的精度满足生产所需的要求。

1.1 GLAS测高数据筛选和精度验证

激光测高卫星发射的激光脉冲在往返大气传输过程中，激光测距值易受大气、云层、地表反射率、硬件动态响应范围等因素影响，导致其测距精度下降[12]。文献[5]研究发现，利用30 m分辨率的SRTM DEM数据(SRTM-GL1)作为限制条件[12]和GLA14标准数据记录的质量评价参数进行筛选，筛选后的GLAS点可以满足1∶50 000高程控制点精度要求。

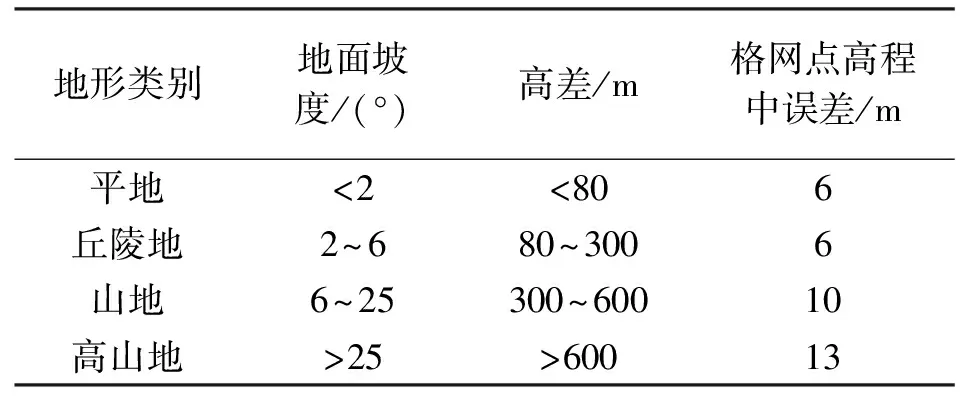
表1 DSM相对于高精度检查点的精度要求

此次GLAS精度验证区域位于陕西省中东部，地处关中盆地，地势平坦。经过GLAS高程控制点筛选后，共保留了431个激光高程点。利用机载LiDAR数据对激光高程点进行检验，试验结果见表2，高程差平均值为-0.249 m，中误差为0.776 m，其中高差绝对值小于1.0 m的点占89.79%。剩下10.21%的点误差大于1 m，主要是由于GLAS点的获取时间和LiDAR数据的获取时间不一样，高程已经发生变化。上述试验验证了筛选后的GLAS高程控制点满足精度要求，可以作为控制资料评估境外DSM的高程精度。

表2 高程差绝对值在各区间段内的占比

1.2 DSM精度优化模型

DSM模型改正中主要采用的方法是点对面模型[9,13]，首先利用筛选后的控制点求解DSM与控制点之间的高差Δh；利用最小二乘法拟合Δh与DSM经纬度x、y之间的系数，即Δh=f(x,y)；然后，将x、y代入f(x,y)中求得改正后的Δh′。本文针对f(x,y)提出线性和二次多项式改正模型。试验发现，个别试验区域存在正数个数和负数个数明显相差甚远的问题，因此提出偏度和中值改正模型。

1.2.1 偏度优化模型

试验中分别以原始高差Δh、Δh个数为横轴和纵轴，频数呈正态分布，偏度(skewness)是反映高差和高差个数之间非对称程度的指标[14]，偏度可以有效地度量高差分布对称性的偏移程度。本次试验以偏度skewness作为改正值，具体优化模型如下

(1)

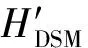
1.2.2 中值优化模型

中值能将数据集划分为相等的上下两部分，代表离散数列的分布状态，在不受极值的影响下反映数列的偏态。本试验将高差按大小顺序进行排列，取中值median作为改正数，具体优化模型如下

(2)

1.2.3 线性优化模型

统计回归模型是刻画变量间依赖关系的模型[15]，本试验用线性改正模型对Δh与(x,y)进行回归分析，模型假设如下所示

(3)

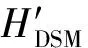
1.2.4 二次多项式优化模型

用二次多项式对Δh与(x,y)进行回归分析，改正模型如下所示

(4)

2 分析与讨论

试验区哈萨克斯坦地形复杂，特点是东南高、西北低。试验地区的图幅编号分别为M43、M44、M45，位于哈萨克斯坦的中东部，M43为整体地势平坦的平地地貌，M45为崇山峻岭、地势陡峭的高山地貌，M44为过渡地带的丘陵地貌，从东往西地势逐渐趋于平坦。

2.1 境外DSM高程精度验证试验结果

由于试验区域水系众多且变化无常，无法将所有水域点进行人工删除，因此本文仅除去落入大面积水域、海域和境外的GLAS点，原始激光点不做其他人工筛选，对GLAS和DSM之间的高程差进行统计分析，结果见表3，GLAS点位空间分布如图2所示。根据表1高精度控制点检查需满足的精度要求，得出以上区域DSM误差均在限差范围内。研究发现，M43和M45均值和中误差都较大。M45区域主要以高山区为主，存在大面积常年积雪，会出现高反射率[16]，因而导致信号饱和或异常，同时激光经过地面反射返回卫星过程中，一部分激光脉冲会受到云、雾的影响出现前向散射，造成脉冲回波存在展宽和拖尾效应，影响高程测量误差[17]。M43是由于小面积水域众多，而且水域范围逐年变化，试验中无法删除，在DSM匹配时发现粗差点较大，说明水域对DSM匹配精度影响较大。虽然通过筛选能满足精度要求，但仍存在一定系统误差，可通过模型改正提高DSM绝对高程精度。

表3 哈萨克斯坦原始数据和筛选后数据统计结果

2.2 DSM改正模型试验结果

首先对各个试验区做高程差和个数的频数分布图，如图3所示。

统计各个区域的正数个数和均值、负数个数和均值、偏度、中值，见表4。

正数个数正数均值/m负数个数负数均值/m偏度/m中值/mM43615742.5776731-1.0702.252.180M44355841.66412683-0.9470.500.857M4519192.624157-2.4013.002.614

M43拟合得到的线性和二次多项式模型为

(5)

M44拟合得到的线性和二次多项式模型为

(6)

M45拟合得到的线性和二次多项式模型为

(7)

由上述试验可得，不同区域的平均值在改正后都小于1 m。各个区域都存在正负个数相差甚远的情况，M43正数个数是负数个数的9.148倍，M44正数个数是负数个数的2.806倍，M45正数个数是负数个数的12.223倍，M43和M45在频数分布图上存在明显的偏度。通过模型改正后，4种模型均能有效减少系统误差，平地地貌M43和丘陵地貌M44利用二次多项式改正后效果最优，而高山地貌M45利用线性模型改正后效果最优。

表5 不同模型改正后统计结果 m

3 总结与展望

本文利用机载LiDAR数据验证了筛选后的星载激光测高数据(GLAS)的精度，然后利用GLAS星载激光测高数据优化了DSM的高程精度，并提出了优化境外DSM的技术流程。由于高山区和水域对DSM高程匹配产生较大影响，使得试验区M45和M43的中误差和均值较大。本次试验选用的改正模型分别为偏度、中值、线性和二次多项式改正模型，4种模型对试验区都有较大的改善，其中二次多项式改正模型适合于平地地貌和丘陵地貌，线性模型适合于高山地貌。

希望本研究能对国产星载激光卫星的应用提供一些参考与借鉴。在未来境外DSM生产中，采用卫星激光高程控制点可用于前期发现系统误差和大规模DSM产品的精度优化提升。