基于混凝土细观骨料模型的SHPB仿真模拟研究
郭瑞奇, 任辉启, 张 磊, 龙志林, 吴祥云, 李泽斌
(1. 湘潭大学 土木工程与力学学院,湖南 湘潭 411105; 2. 军事科学院 国防工程研究院,河南 洛阳 471023)
混凝土是常见的工程材料,对防护工程而言需要考虑其动态力学性能。分离式Hopkinson压杆(Split Hopkinson Pressure Bar,SHPB)实验系统是广泛应用于测试材料动态力学性能的装置,可实测材料在高应变率(102~104s-1)下的应力应变曲线,也是研究混凝土材料动态力学性能的最基本的实验手段。现今已有诸多学者利用不同直径的SHPB装置对混凝土材料进行了实验研究[1-4]。
而随着数值分析技术以及高速计算机的快速发展,有部分学者开始利用有限元分析技术来取代部分实验,并利用数值仿真的方法来模拟SHPB实验过程,从而定性地研究混凝土材料的动态力学性能,如巫绪涛等[5-6]模拟了用于混凝土冲击试验的O/100 mm的SHPB装置,并讨论了应力波在该装置中的传播特性以及罚函数算法中罚因子合理数值的选取问题;贾彬等[7]模拟了中国工程物理研究院结构力学研究所O/50 mm的SHPB实验系统,确定了一套混凝土HJC(Holmquist-Johnson-Cook)模型参数确定方法;余道兴等[8]分别运用了K & C(Karagozian and Case),HJC和CSC(Continuous Surface Cap)三种材料模型对混凝土的SHPB试验进行模拟。然而大多数研究都是从宏观水平上将混凝土试件视为均匀材料,典型的如图1所示。

图1 将混凝土试件视为均匀材料的数值模拟[9]Fig.1 Uniform numerical model of concrete
由于混凝土是一种非均匀材料,其内部含有大量随机分布的粗骨料颗粒,用SHPB对混凝土进行实验时不可避免地要面对非均匀性问题。这种非均匀性问题主要来自于两个方面:一方面是由夹杂颗粒导致的材料非均匀性;另一方面是应力波效应,SHPB实验不考虑试件中波的传播,也就是两个基本假定之一——“短试件的应力/应变沿其长度均匀分布(动态平衡)[10]”,这对于常规的金属材料是易于满足的,而对混凝土材料而言,波在“骨料——砂浆基体”界面传播时会存在复杂的反射和透射,因此使用均匀的混凝土模型来模拟SHPB实验或许与真实实验结果有些偏差。
本文将混凝土视为由砂浆基体和粗骨料组成的双相复合材料,将骨料简化为球形,建立了圆柱状三维混凝土随机骨料模型。以O/100 mm的SHPB实验装置为例,建立了整体实验装置的有限元模型,并通过数值模拟的方法从细观层次上研究非均匀模型在SHPB仿真模拟中的有效性。通过五种不同的梯形波加载以及五种不同骨料含量模型的计算研究了应变率及骨料含量对混凝土动态强度和应力均匀性的影响。最后建立了四种不同骨料尺寸的混凝土模型,并分析了骨料尺寸对模拟结果的影响。
1 混凝土细观骨料模型的建立
近十几年来,从Wittmann等[11]提出的二维多边形骨料模型到Sheng等[12-13]提出的三维凸多面体随机骨料模型,逼近真实混凝土材料的高含量细观骨料模型的建模方法已经较为成熟,作者也对混凝土细观骨料模型的建立、求解算法和求解效率进行了相关研究[14-16]。近年来,已有学者开始利用细观模型对钢筋混凝土梁的抗冲击性能[17]、混凝土的抗侵彻性能[18]以及钢纤维混凝土的动态强度[19]进行了数值模拟研究。
本文采用郭瑞奇等研究中的方法,建立了二级配圆柱状三维混凝土骨料模型,其中小石粒径为5~20 mm,中石20~40 mm,体分比为55∶45。为了保证所生成的骨料颗粒不超过给定的圆柱区域,需要对球心坐标公式进行修正
(1)
式中:R为圆柱底面半径;Ri为第i颗骨料的半径;ZB和ZT分别为圆柱体底部和顶部边界坐标值;rdm1,rdm2,rdm3分别为位于(0,1)之间的三个独立随机数。
首先在Fortran程序中随机生成ANSYS参数化建模所需要的命令流,建立几何模型以后使用Hypermesh进行有限元网格剖分,最后使用LS-DYNA进行有限元计算,整个模型建立的流程如图2所示。

图2 混凝土细观骨料模型建立流程图Fig.2 Flow chart of the concrete aggregate model
以简单的球形骨料为例,建立了骨料含量为46.06%的混凝土模型,整个试件厚度为50 mm,底面半径为50 mm,由于细观骨料模型的高度几何复杂性,选用solid168十节点四面体单元进行网格剖分。入射杆长5 m,透射杆长3 m,直径均为100 mm,对于这种规则形状采用solid164六面体单元映射网格划分。有限元模型建立的各个阶段如图3所示,依次是几何模型、骨料颗粒网格剖分、砂浆基体网格剖分和整体有限元模型x=0 mm(中心轴线处)截面示意图。

图3 数值模型建立过程Fig.3 Modeling procedure of the numerical model
2 混凝土细观骨料模型有效性验证
为了验证混凝土细观骨料模型用于SHPB仿真实验的有效性,以上文建立的骨料含量46.06%的混凝土试件为例,进行动力学模拟分析,并将结果与实际实验数据进行比较。
2.1 材料本构模型及参数选择
HJC本构模型常用于混凝土材料的动态力学仿真中,使用特征化等效应力对HJC强度模型的描述为
(2)

HJC模型状态方程分为弹性压缩(OA段)、压实变形(AB段)和密实后变形(BC段)三个阶段,如图4所示。

图4 HJC材料模型状态方程曲线Fig.4 Equation of state curve for HJC model
方秦等[20]从塑性屈服面理论出发,合理确定了岩石材料的HJC本构模型参数,因此本文首先由文献[21]中的数据分别确定骨料和砂浆基体的HJC材料参数,然后根据方秦等研究中对花岗岩材料的研究对骨料参数进行修正,砂浆的模型参数和骨料的修正数据分别如表1和表2所示,计算时统一换算成cm-g-μs单位制。

表1 砂浆HJC模型参数Tab.1 HJC model parameters for mortar

表2 花岗岩HJC模型参数修正值Tab.2 HJC model parameters revised for moorstone
本文并未引入额外的失效准则来控制单元失效,仅使用HJC模型中自带的失效类型参数作为单元的破坏准则,即FS=0.002。 入射杆和透射杆采用线弹性模型,取弹性模量E=200 GPa, 密度ρ0=7.8×103kg/m3, 泊松比ν=0.3。在三种材料之间分别设置三对接触,其中骨料与砂浆之间采用面面固连接触,接触刚度罚因子取默认值。另外两种采用自动面面接触,罚因子参照巫绪涛等的研究取为“2.0”。
2.2 加载计算及试件应力均匀性分析
由于混凝土细观骨料模型的几何复杂性,无法采用对称模型。在SHPB仿真模拟中为保证求解精度,整体模型单元数量较多,计算规模较大,因此本文采用直接在入射杆端部施加应力脉冲的方式加载。
在杆端z=0处分别作用图5所示的五种不同梯形脉冲,分作两组对比实验。第一组为加载时间相同但应力幅值不同的三种梯形荷载,分别为σ1=100 MPa,σ2=150 MPa,σ3=200 MPa, 其上升沿为60 μs,总加载历时为240 μs。第二组为应力幅值均为100 MPa但加载时间不同的三种梯形载荷σ1,σ′1,σ″1中上升沿分别为60 μs,80 μs,120 μs,总加载历时分别为240 μs,360 μs,480 μs,程序总计算时间2 400 μs。

图5 五种不同的梯形载荷Fig.5 Five kinds of trapezoidal loads
在Hopkinson杆实验中,试件内部的应力均匀与否是影响实验结果有效性的一个重要因素。应力均匀性假定对于金属类均质材料往往是易于实现的,而对于混凝土材料而言,其试件厚度比一般金属类材料大了一个量级,且具有破坏应变小、含有粗骨料夹杂颗粒、波速较低等特点,因此必须对其在实验过程中的应力均匀性进行分析,以验证实验结果的有效性。通过比较试件两端的应力历史即可检测其应力平衡过程,因此研究人员先后提出了类似的应力差之比的公式作为试件应力平衡的准则[22-23]
(3)
式中:σ1(t)和σ2(t)分别为试件前后端面的应力历史, 应力平衡因子δ(t)已经被一些学者用于评估SHPB实验中试件的应力均匀性问题[24], 通常认为δ(t)<0.05时试件达到了较好的应力平衡状态。
相对于均匀的混凝土模型而言,细观骨料模型更能逼近真实的试件结构。本文在对混凝土细观骨料模型用于SHPB仿真实验的结果分析之前,首先对试件在应力波作用过程中的应力均匀性进行研究。
在试件前后端面取三对单元,它们与中轴线的距离分别为0 mm,25 mm,50 mm,三种载荷作用下的应力平衡因子—时间曲线如图6所示。可以看到在100 MPa的梯形载荷作用下试件的整体应力均匀性相对较好,在1 070 μs左右达到应力平衡最低点以后,δ(t)处于小幅震荡状态。同时从“3.1”节的相关结果中可以看到,在1 200 μs左右时由于试件表面开始出现宏观裂纹,最外侧单元的δ(t)出现了波动。除此之外,在应力波作用的大部分时间里,试件内外单元的应力平衡因子变化趋势都相对稳定。而在另外两种较高幅值的梯形载荷作用下,试件的应力均匀性相对较差,由于宏观裂纹的过早出现,整个试件难以保持稳定的应力平衡状态,内外单元的应力平衡因子到达最低点以后便开始剧烈震荡,而且试件破坏越严重,这种震荡就越剧烈。
此外,无论哪种载荷作用下,试件达到应力平衡状态(δ(t)≤0.05)或应力平衡因子到达最低点都需要一段较长的时间(不低于100 μs)。这表明在实际实验中,应该在保证达到目标应变率的前提下,适当延长应力脉冲升时,从而使混凝土试件有充足的时间达到应力平衡状态。

图6 不同幅值载荷作用下试件的应力平衡因子Fig.6 Balance factor of the concrete specimen under different loads
2.3 模型有效性验证
取入射杆和透射杆中部单元作为数据采集点,由LS-DYNA计算出的五种轴向应力波形如图7所示。
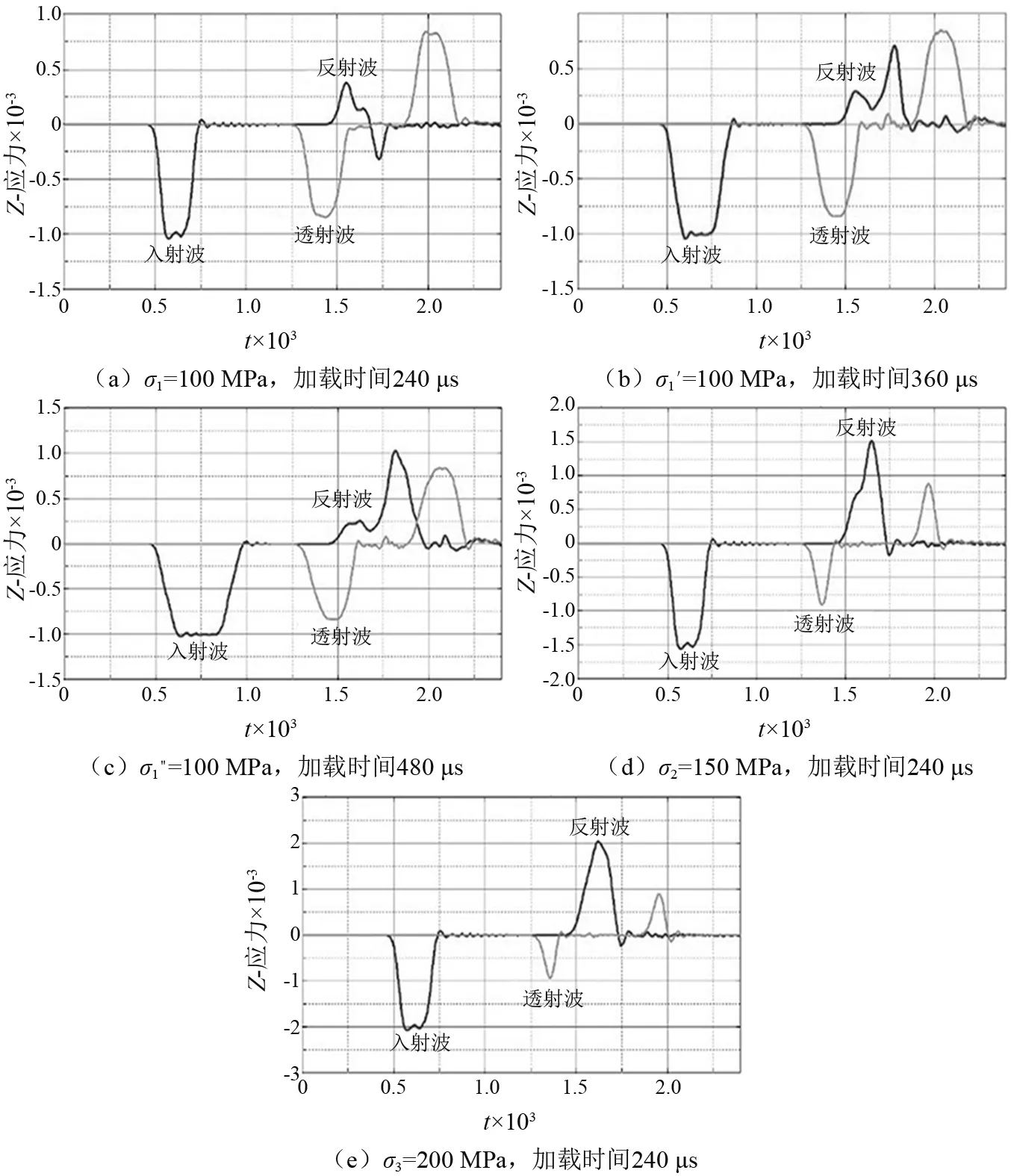
图7 五种不同的梯形载荷作用下入射杆和透射杆 中部单元轴向应力波形Fig.7 Axial stress wave of the middle elements in incident bar and transmitted bar under five kinds of trapezoidal loads
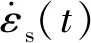
(4)
(5)
(6)
式中:A0为杆的横截面积;As和ls为试件的横截面积和长度;E0和c0分别为入射杆的弹性模量和波速。首先通过式(5)求得试件在五种载荷作用下的应变率—时间曲线,如图8所示。
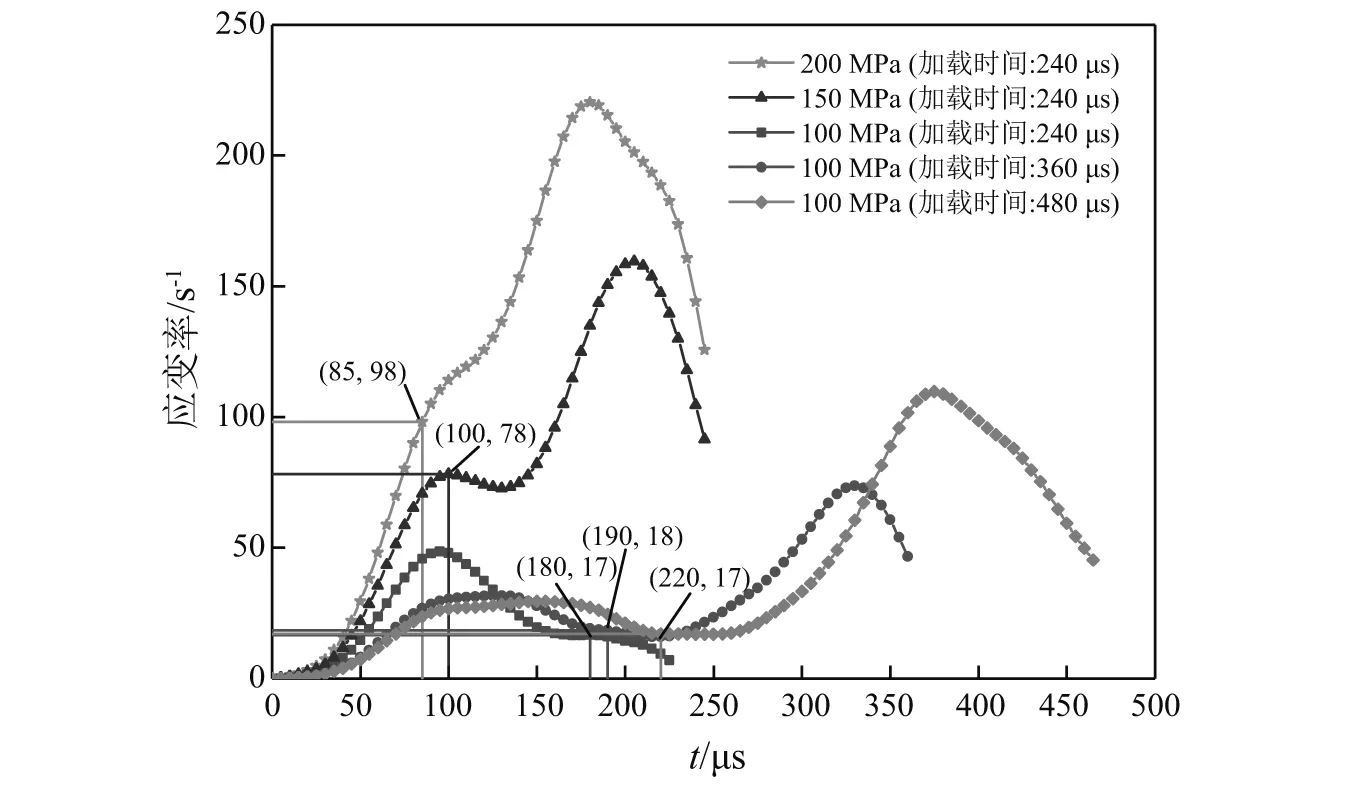
图8 混凝土试件的应变率-时间曲线Fig.8 Strain rate-time curve of concrete specimen
从图7和“3.1”节内容中可以看到,随着应变率的提高,混凝土破坏后反射波信号会快速增加,直接处理得到的应变率曲线将不正确。因此,我们在图8中标注了混凝土细观骨料模型细小损伤出现的时间点,在混凝土破坏之前的应变率才是混凝土试样的主要加载应变率。使用幅值为100 MPa的三种梯形脉冲加载时,试件在应力波作用阶段其应变率主要位于20~50 s-1,随着载荷作用时间的增加,试件的应变率相对而言更加稳定。而当加载脉冲幅值为150 MPa及200 MPa时,试件的应变率主要位于50~100 s-1,虽然这两种载荷升时均为60 μs,但应力幅值越高,加载脉冲上升沿越陡,应变率曲线的平台段也越短,难以实现恒应变率加载。通过式(4)和式(6)分别求出试件的应力—时间曲线和应变—时间曲线后,消去时间轴即可得到试件的平均应力—应变曲线。巫绪涛等和吕太洪等[26]给出了混凝土材料在SHPB实验中得到的4个应变率下的应力—应变曲线,刘传雄等[27]也对骨料尺寸为15~20 mm的混凝土材料试样进行了应变率范围30~180 s-1的动态压缩实验。本文首先将加载时间为240 μs而应力幅值不同的三种波形作用下混凝土试件的动态应力应变曲线进行比较,然后参考文献中对应应变率范围内的应力应变曲线,将实验数据与数值模拟的结果进行比较分析,如图9所示。

图9 仿真模拟结果有效性验证Fig.9 Validation of analog simulation results effectiveness
由于应力波的传播速度远高于裂纹扩展的速度,会使混凝土试件表现出“应变滞后效应[28]”,在图9(a)所示的三种不同应变率下混凝土试件的应力应变曲线上表现为应力相同时试样的应变随着应变率的提高而降低,也就是材料动态弹性模量随应变率的提高而逐渐增大(应变率效应)。幅值为150 MPa的梯形波作用下试件的应力应变曲线与100 MPa的结果相比,应力峰值没有明显变化,但是试件的动态弹性模量有所增强,且卸载段由黏弹性回滞现象变为应变软化现象。在冲击荷载作用下,混凝土材料内部同时出现应变率硬化和损伤软化效应,从这两种载荷作用下试件应力应变曲线的比较可以看到,应变率的提高使得软化效应更为明显,损伤效应和应变率硬化效应达到平衡,这种饱和现象在这里表现为应力峰值并没有明显地随应变率的提高而增加,王道荣等[29]对骨料颗粒较大的混凝土材料进行SHPB实验时也发现了同样的现象。幅值为200 MPa的梯形波作用下试件的应力应变曲线与150 MPa的结果相比,试件的动态弹性模量和应力峰值都有所提高。
通过实验数据与仿真结果的比较可以看到,由于不同研究人员所采用的实验装置各不相同,而且制作的混凝土试件其骨料类型、骨料含量等都具有一定的随机性,所以实际的试验数据本身也有一定的区别。与刘传雄等研究中的结果相比,本文通过仿真模拟所得的应力应变曲线在弹性阶段和卸载段都相对较陡,我们认为前者的主要原因是混凝土试件在实际加工制作中必然会存在一定的平行度公差,这样会导致实验测得的弹性模量较低,而模拟中试样两端是理想状态下绝对平行的,因此曲线在弹性阶段相对较陡。后者是由于在仿真模拟中,当单元达到破坏应变后被删除,所形成的孔洞和裂纹不会被填补,而实际实验中混凝土存在一个压紧密实的过程,因此其曲线在卸载段相对缓和。除此之外,尽管数值模拟中的加载波形、材料参数及实验装置与实际实验有所不同,但使用混凝土细观骨料模型仿真所得到的应力—应变曲线,其体现的动态力学行为与实验结果是十分相近的,包括应变率较低时出现的黏弹性回滞现象(见图9(b))和应变率较高时的损伤软化现象(见图9(c)),因此使用混凝土细观骨料模型可有效模拟SHPB实验并反应材料的动态力学性能。
3 不同应变率及骨料含量对模拟结果的影响与分析
3.1 不同应变率下混凝土细观骨料模型的破坏描述
图10和图11给出了幅值为100 MPa的梯形载荷作用下应力脉冲由入射杆末端穿过短试件进入透射杆的整个过程:t=980 μs时,应力波到达入射杆末端,即将进入混凝土试件;t=1 020 μs时,应力波刚刚穿过混凝土试件,由于材料的不均匀性,可以看到整个试件轴向应力的不均匀分布,且透射波波阵面已不再保持为平截面;t=1 060 μs时,试件两端面开始出现应力集中现象,且端面有部分损伤出现;t=1 160 μs时,试件表面开始出现应力集中现象,试件与入射杆和透射杆接触面出现明显损伤;t=1 200 μs时由于骨料与砂浆之间的相互作用,试件表面出现应力集中现象的部位开始出现条状锯齿样裂纹;t=1 380 μs时,应力脉冲已经穿过试件。

图10 应力波作用于混凝土细观骨料模型过程的应力云图Fig.10 Stress nephogram of concrete model with mesoscopic aggregates subjected to stress wave
随着加载幅值和应变率的升高,混凝土细观骨料模型表面裂纹的演化更加明显,细观骨料模型的破坏过程主要表现为试件两端和表面出现的细小损伤沿粗骨料间隙的扩展与延伸。幅值150 MPa和幅值200 MPa梯形载荷作用下1 200 μs时试件与粗骨料的轴向应力云图分别如图12和图13所示,可以看到,加载幅值越高,损伤演化越迅速,同一时间下高幅值加载时试件表面的裂纹已经开始融汇贯通,破坏更严重。同时从图7中也可以看到,试件的迅速破坏会导致波阻抗降低,透射波随之减小,相应的反射波会快速增加。

图11 不同时间下混凝土细观骨料模型的应力云图Fig.11 Stress nephogram of concrete model with mesoscopic aggregates at different times

图12 幅值150 MPa梯形载荷作用下混凝土试件应力云图Fig.12 Stress nephogram of concrete specimen subjected to trapezoidal load with the amplitude of 150 MPa

图13 幅值200 MPa梯形载荷作用下混凝土试件应力云图Fig.13 Stress nephogram of concrete specimen subjected to trapezoidal load with the amplitude of 200 MPa
3.2 不同骨料含量对试件应力均匀性及动态强度的影响
为了研究粗骨料含量对混凝土试件的应力均匀性及动态强度的影响,建立了四种不同骨料含量的混凝土细观骨科模型(见图14),模拟过程中统一施加σ1=100 MPa的梯形载荷,按照上文所述的方式计算出每种试件的应力平衡因子,结果如图15所示。

图14 四种不同骨料含量的混凝土模型Fig.14 Four concrete models of different aggregates content

图15 骨料含量对试件应力平衡性的影响Fig.15 Effects of aggregates content on stress uniformity of concrete specimen
由于每种模型中的骨料为随机分布,在试件两端面所取单元应力时程计算出的应力平衡因子只能反映出局部的平衡状态,从图15中可以看到试件内外单元的应力平衡性好坏并没有明显的规律性。但是结合图6(a)可以发现,随着骨料含量的增加,混凝土试件越来越密实,试件内外的应力平衡变化逐渐趋于一致,试件整体的应力均匀性更好。
除了一些轻骨料混凝土和珊瑚骨料混凝土,通常粗骨料的强度要高于水泥石的强度以及混凝土的系统强度,这种情况下适当增加骨料含量能够起到提高混凝土整体强度的效果。取入射杆和透射杆中部单元的应力波形做出每种试件的应力应变曲线,如图16所示。结果表明,随着骨料含量的增加,试件的动态弹性模量和峰值应力都有所提高。随着试件整体动态强度的提高,产生单位变形所需要的能量增加,在图16中表现为同一载荷作用下,骨料含量越高则试件所能达到的最大应变逐渐减小。

图16 骨料含量对混凝土试件动态强度的影响Fig.16 Effects of aggregates content for dynamic strength of concrete specimen
3.3 骨料尺寸对试件应力均匀性及动态强度的影响
为了研究粗骨料尺寸对混凝土试件的应力均匀性及动态强度的影响,建立了四种不同骨料尺寸的混凝土细观骨料模型(见图17)。为了避免骨料含量对结果的影响,将骨料体积率控制在30%左右,四种试件的相关参数见表3。

图17 四种不同骨料尺寸的混凝土模型Fig.17 Four concrete models with aggregates at different size

试样编号骨料粒径范围/mm最小粒径最大粒径骨料含量/%骨料个数a51030.02472b101530.09119c152030.1245d202530.7321
从上面可以看到骨料尺寸越小,在体积率相同的情况下其颗粒数量大大增加,在试件内部的分布就越近似于均匀状态。四种试件的应力平衡因子—时间曲线如图18所示,随着骨料尺寸的减小,试件的应力平衡因子在到达低点以后变化更趋于稳定。而且相对于大尺寸骨料的混凝土模型而言,小尺寸骨料混凝土模型内外应力平衡因子趋势的一致性更好,表明其整体应力均匀性更好。
四种模型的应力应变曲线如图19所示,可以看到骨料粒径在10~25 mm内的三个试件动态强度没有明显区别,而且与图16中骨料含量30.25%的二级配混凝土模型的动态应力应变曲线重合度较高。但是当骨料尺寸在5~10 mm内时,含量为30.02%的混凝土动态弹性模量已经相当于骨料含量40.78%的二级配混凝土,所能达到的应力峰值相当于骨料含量为46.06%的二级配混凝土。

图18 骨料尺寸对试件应力平衡性的影响Fig.18 Effects of aggregate size on stress uniformity of concrete specimen

图19 骨料尺寸对混凝土试件动态强度的影响Fig.19 Effects of aggregate size for dynamic strength of concrete specimen
我们对骨料尺寸为5~10 mm内的混凝土模型以及20~25 mm内的混凝土模型进行比较分析,做出1 200 μs时沿试件中心轴线处的截面图以及对应的轴向应力云图,如图20所示。由于本文采用了较为坚硬的花岗岩骨料,混凝土的破坏形式表现为裂纹全部绕骨料与砂浆的界面进行扩展,而骨料本身没有破坏。这种情况下骨料尺寸的增加会引起骨料周围较为严重的应力集中现象,在应力波作用过程中会产生更多的微裂纹,从而降低混凝土的整体强度。而骨料尺寸较小的情况下,数量较多的骨料在试件内部的分布更均匀,这样能够使骨料充分受力从而更好地发挥其强度以及骨架作用。
除此之外,实际实验中混凝土材料在养护时由于骨料和砂浆的收缩不同会产生大量的微裂纹。随着骨料尺寸的增加会导致其与砂浆模量的差别更加明显,产生更多的初始裂纹,从而进一步降低混凝土材料的整体强度[30-31]。

图20 1 200 μs时不同骨料尺寸的混凝土模型应力云图Fig.20 Stress nephogram of concrete models with different aggregate size at 1 200 μs
4 结 论
本文建立了圆柱状三维混凝土细观骨料模型,并将其应用于SHPB的仿真实验中。通过五种不同梯形载荷的加载计算,得出了试件不同应变率下的应力—应变曲线,并将模拟结果分别与相应应变率下的试验结果进行对比分析,验证了本文所建立的混凝土细观骨料模型用于SHPB仿真实验的有效性。
通过对比试件在三种不同幅值载荷作用下的应力平衡因子发现,在较低幅值梯形载荷作用下试件的整体应力均匀性相对较好,在应力波作用的大部分时间里,试件内外单元的应力平衡因子变化趋势都相对稳定。而在另外两种较高幅值的梯形载荷作用下,试件的应力均匀性相对较差,由于宏观裂纹的过早出现,整个试件难以达到应力平衡状态,内外单元的应力平衡因子到达最低点以后便开始剧烈震荡,而且试件破坏越严重,这种震荡就越剧烈。在实际实验中,应该在保证达到目标应变率的前提下,适当延长应力脉冲升时,从而使混凝土试件有充足的时间达到应力平衡状态。
对五种不同骨料含量混凝土模型的计算分析结果表明,在一定的范围内随着骨料含量的增加,试件内外的应力平衡变化逐渐趋于一致,试件整体的应力均匀性更好;骨料含量越高,混凝土试件整体的动态强度越高,但同时所能达到的最大应变也逐渐减小。
对四种不同骨料尺寸混凝土模型的计算分析结果表明,当骨料尺寸减小到一定程度时,相同体积率下骨料数量大大增加,分布更加均匀。试件的应力均匀性更好,强度更高。
此外,本文所建立的基于细观骨料模型的SHPB整体试验装置有限元模型,只需改变相应的材料类型和相关参数,其同样适用于泡沫铝、珊瑚砂、礁灰岩等多孔材料和含夹杂颗粒的非均质材料的仿真实验研究,为多种材料的SHPB细观数值模拟提供方便。

