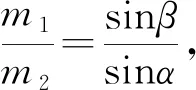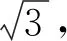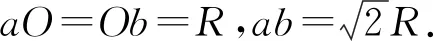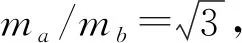等效转换 举重若轻——例谈一类静力学试题的巧解

罗春焱 傅 礼

(重庆市綦江区三江中学,重庆 401431)

通常处理轻绳、轻杆、球连接体静力学平衡问题都是应用相似三角形知识来解决的．在新一轮高三物理复习中,笔者用等效方法,借助杠杆平衡条件等知识进行分析,取得了良好的教学效果.下面列举几例与大家分享.

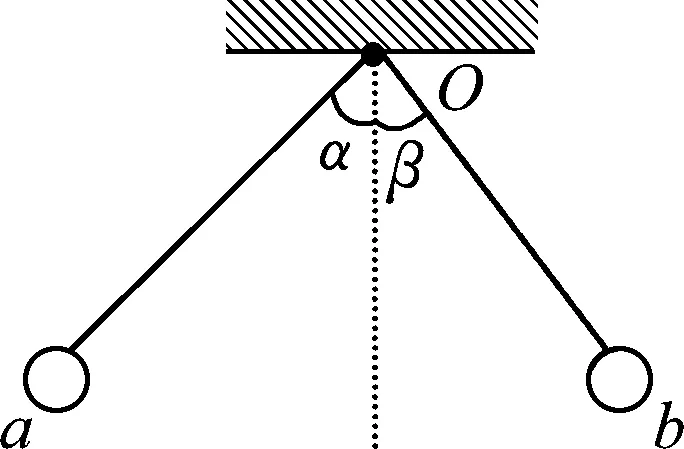
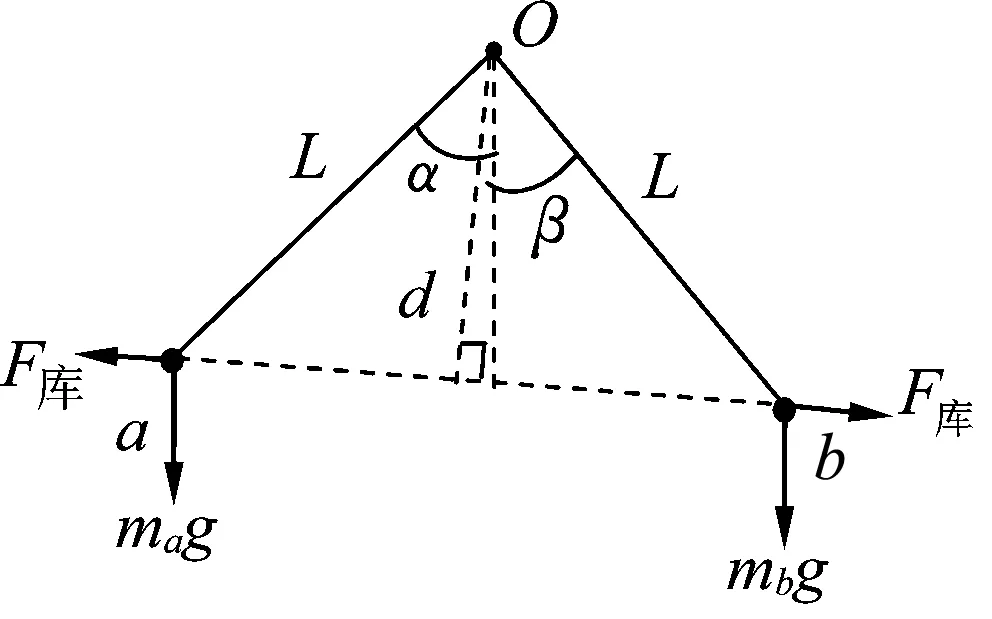
图1

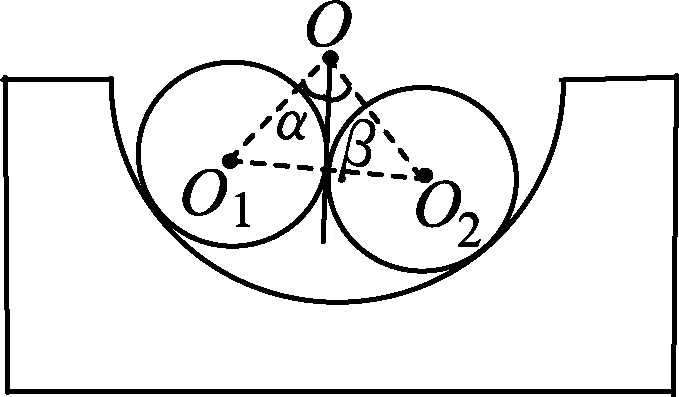
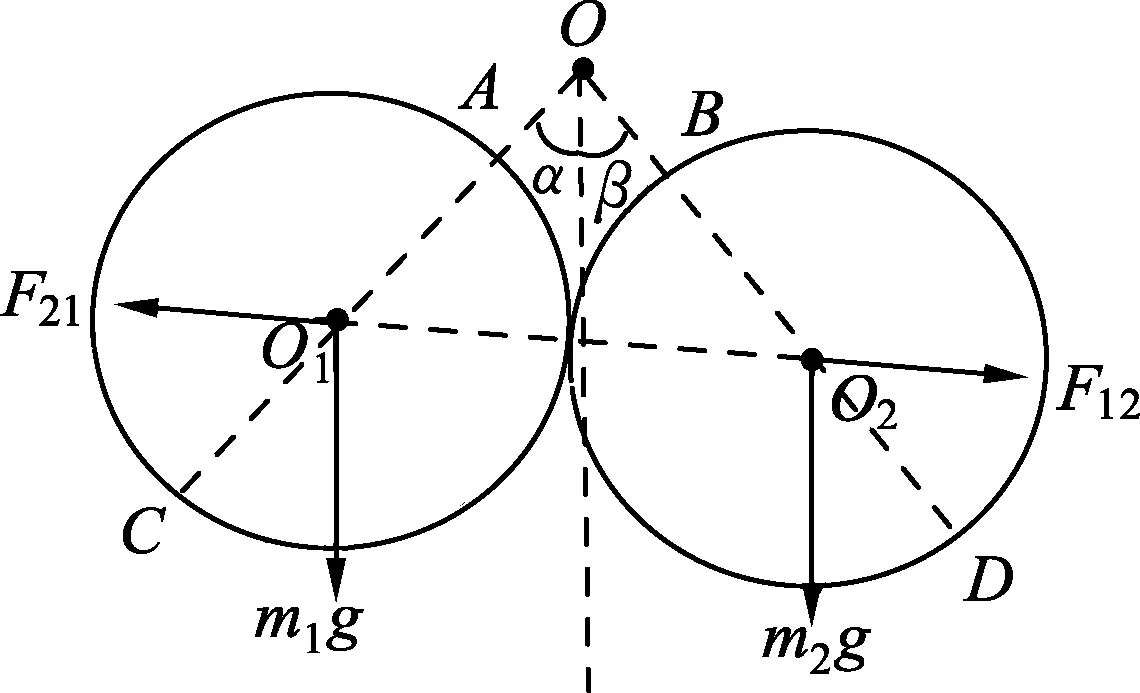
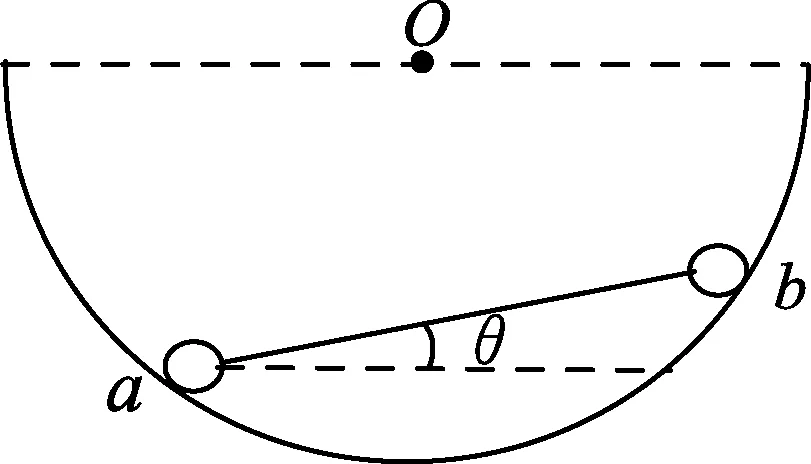
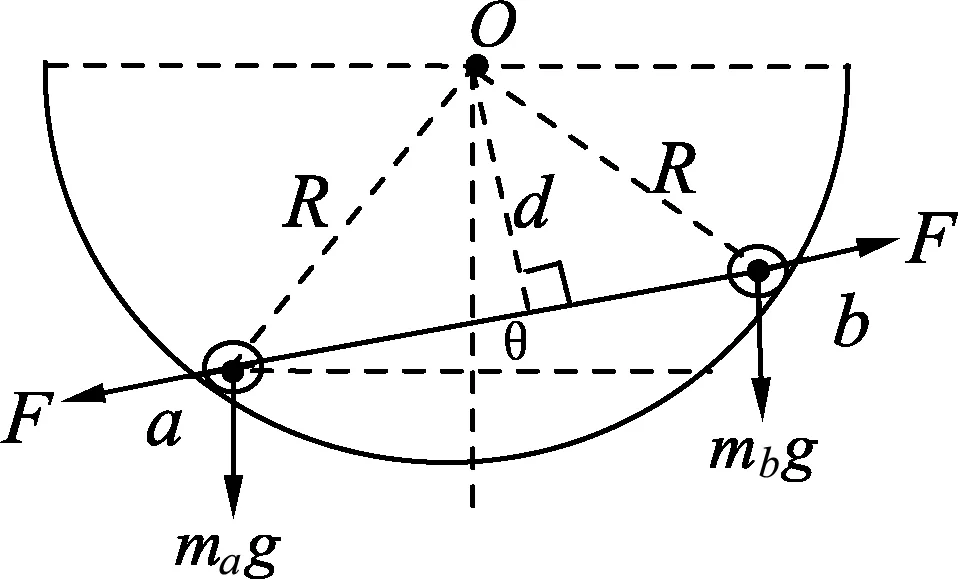
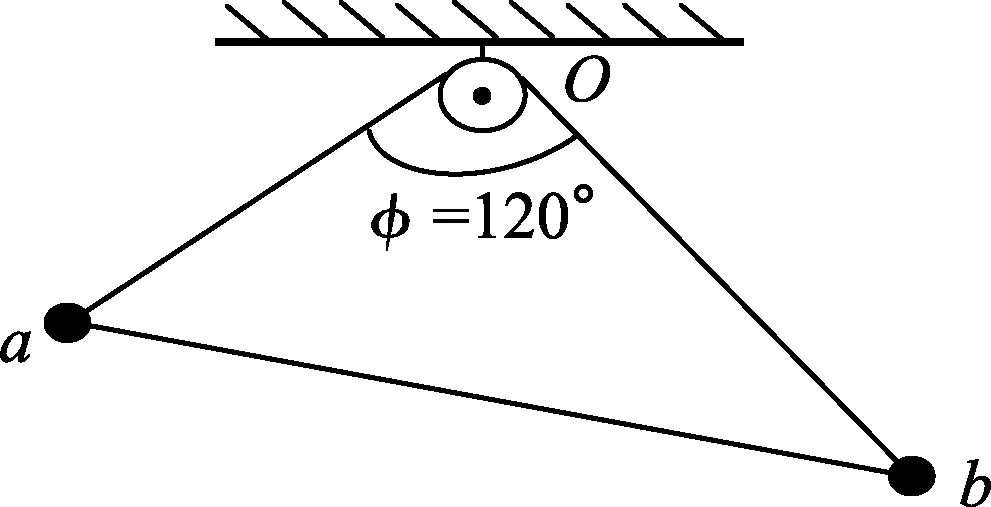
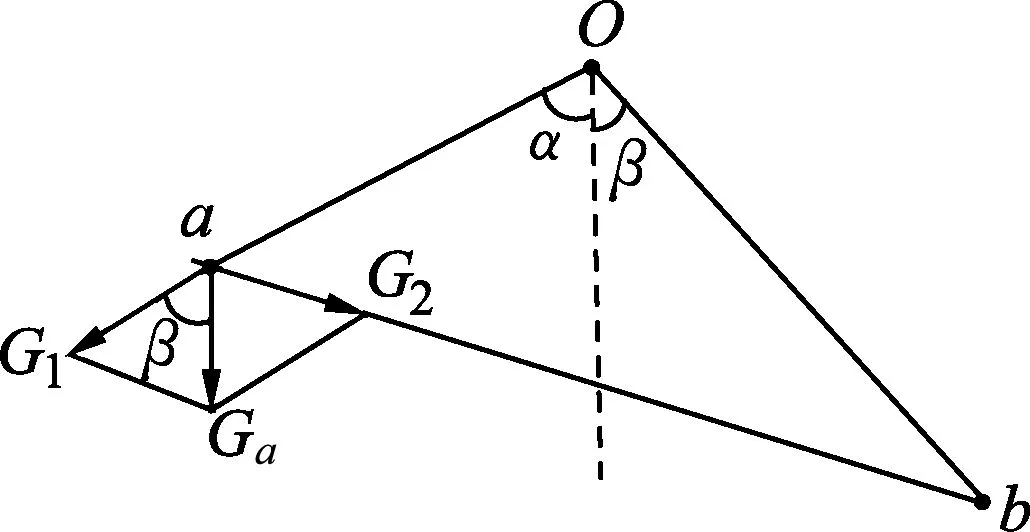
例1.用等长的丝线把两个带电小球挂在同一点O上,小球a的质量为ma,小球b的质量为mb,ma

(A)α>β. (B)α=β.

(C)α<β. (D) 无法确定α与β的大小.

图2

解析:对a、b两小球进行受力分析知,aO、Ob是两拉直的丝线,我们可以把aOb整体视为一根可绕O转动的硬棒．即aOb就是以O为支点的杠杆，等效图如图2所示.设O到a、b两球连线的距离为d,线长为L.由于两球之间的库仑斥力大小相等、方向相反且力臂d相同,对杠杆的转动无力矩贡献．

由杠杆平衡条件,有magLsinα=mbgLsinβ．

点评:学生见到此题后,大多数用隔离法分别对a、b进行受力分析,然后用相似三角形建立方程加以解决,显得非常繁琐．利用等效转换,借助杠杆平衡条件求解则轻松自如．

图3

例2.如图3所示,在圆弧形凹槽里放两个大小相同的光滑金属球O1、O2,它们的质量分别为m1、m2,O点是圆弧槽的球心,静止时,O1O连线与竖直线夹角为α,O2O连线与竖直线夹角为β．试证明:

解析:如果我们将O1OO2连线整体虚拟成一根可绕O点转动的硬棒,则这个平衡系统可以用等效杠杆O1OO2来替代．如图4所示,假设O1、O2两球与凹槽的接触点分别为C、D,连接CO、DO.

图4

分别对O1、O2两球进行受力分析知:C、D两点受到凹槽对球的支持力必指向球心O1、O2以及凹槽中心O．故C、O1、A、O必在同一直线上;D、O2、B、O也在同一直线上(A、B分别是CO、DO连线跟球O1和球O2的交点).设球O1对O2的作用力为F12,球O2对O1的作用力为F21,球O1、O2半径为r,O到O1O2的连线的距离为d,凹槽半径为R．由牛顿第三定律知:F12=F21.由于两球之间的作用力大小相等、方向相反且力臂d相同,对杠杆的转动无力矩贡献．

以O为支点,由杠杆平衡条件,得

m1g(R-r)sinα=m2g(R-r)sinβ.

点评:本题若用相似三角形知识证明,比较复杂,改用以上方法,更简洁．

图5

(A) 45°. (B) 30°. (C) 22.5°. (D) 15°.

解析: 对a、b两球进行受力分析,半球面对a、b两球的支持力指向球心O．因此,若将a、b两球用细线与悬点O连接并悬于O点,移开半球面后,则整个系统仍在原空间位置保持平衡．我们可将aOb虚拟成一根硬棒(等效杠杆),支点为O.

图6

由杠杆平衡条件,得

magRcos(45°+θ)=mbgRcos(45°-θ).

点评:本题是2018年四川课标卷第21题,既是一道难题,更是一道好题．应用上述解法可为考生节约有限的考试时间,缓解考生的紧张情绪．

图7

例4.轻杆两端固定两小球a和b,其质量分别为4m和3m,绕过光滑的小定滑轮连接．已知连接a、b两球的绳长为L,当AO、OB之间的夹角φ=120°时(O为小定滑轮跟绳的接触点),整个系统处于如图7所示的位置平衡．

试求: (1) 绳aO、Ob的长度;

(2) 绳子张力的大小;

(3) 杆上弹力的大小．

图8

解析: 设aO、Ob的长度分别为x、y,与竖直方向的夹角分别为α、β; 小滑轮对绳上O点向上的支持力为F,绳子张力T,杆对球的作用力大小为N,O点到杆的距离为d．如图8所示,则有

x+y=L.

(1)

对点O进行受力分析,由正交分解法易得α=β(过程略).因为α+β=φ=120°，所以α=β=60°.

将拉直的细绳aOb虚拟成等效杠杆,O为支点．由于杆对两球的作用力大小相等方向相反且力臂d相同,对杠杆的转动无力矩贡献．

由杠杆平衡条件,有magxsinα=mbgysinβ.故

4x=3y.

(2)

又假设取消小滑轮,用弹簧秤拉住绳上O点,系统仍处于原空间位置平衡,则弹簧秤的读数一定等于力F的大小．而此时弹簧秤所称的重量就是整个系统重力的大小,故有

F=(ma+mb)g=7mg.

(3)

因力F与两绳0a、Ob的张力T的夹角均为120°,由互为120°角的三力作用使O点静止的结论,3个力的大小必然相等．于是有

T=F=7mg.

(4)

图9

按照力的平行四边形定则,将a球的重力Ga分解为G1和G2,如图9所示,a球静止．则有

G1=N,G2=T=7mg.

在△aG1Ga中,由余弦定理,有

G22=Ga2+G12-2GaG1cosα.

(5)

(6)

以上(4)、(6)两式就是(2)、(3)问的答案．

点评:本题是我校2019年3月份高三诊断检测(理综卷)第24题．从考试统计情况看:大多学生由于第(1)问用相似三角形知识求解,花费了较多时间,以致造成第(2)、(3)问没有时间作答;部分优秀学生虽然能得到第(2)、(3)问的结果,却不知道用等效方法进行替换和用互成120°角的三力作用使O点静止的结论,解题步骤冗长,走了不少弯路．