基于切换系统理论的伺服转台摩擦建模与补偿

崔宁豪，张 倩，李国丽

(1.安徽大学 电气工程与自动化学院，合肥 230601；2.高节能电机及控制技术国家地方联合实验室(安徽大学)，合肥 230601；3.教育部电能质量工程研究中心(安徽大学)，合肥 230601)

0 引 言

伺服转台系统是雷达[1]、射电望远镜[2]、激光通信端机[3]和光电云台[4]的重要组成部分。在空间探测领域需要搭载对星敏感器转台的地面标定与检测系统在低速状态下的高跟踪精度[5]；光通信领域为了保障跟瞄转台低速下的快速捕获、精确瞄准及精密跟踪需求，需要满足10”/s的跟踪精度和稳定性条件的跟瞄转台[6]；望远镜转台伺服控制系统中，系统低速区域的精确检测转台位置和速度对实现恒星、卫星稳定跟踪至关重要[7]。摩擦带来的跟踪不精确，极限环等问题会使得转台在运行过程中定位不精确，出现抖动等。

基于模型的补偿方法能更直观、精确地描述摩擦特性， 易于实现补偿控制，已经成为常用的控制方法[8]。文献[9]中基于观测器与前馈控制技术对动态转台进行控制；文 献[10]采用经过线性化处理的Stribeck模型来估算摩擦力的变化趋势；文献[11]提出一种带干扰补偿的模糊积分滑模控制策略，但滑模控制易引起系统“抖振”；文献[12]中使用小波神经网络解决转台伺服系统的跟踪控制问题，但因总结模糊控制的模糊规则困难以及神经网络的计算量较大等因素，使得该算法很难推广。现在迫切需要寻求一种更为有效的方法来补偿摩擦带来的扰动，实现对转台的高精度跟踪。

本文提出了一种基于切换理论的伺服转台补偿和控制方法。首先，通过多组不同速度下的匀速运动实验数据预估静态参数范围，采用遗传算法辨识静态参数；然后，通过预滑阶段的实验数据预估动态参数范围，采用遗传算法辨识动态参数；然后以转台速度和刚鬃形变的程度作为模型切换条件；基于建立的切换模型，使用PID反馈调节和摩擦补偿相结合的控制策略，在此基础上，建立了转台伺服系统实验平台的仿真平台。对比分析了转台伺服系统摩擦补偿前后的实验结果，验证了基于切换摩擦模型理论的伺服转台复合控制策略的有效性。

1 摩擦建模

1.1 基于切换系统理论的摩擦模型

图1 摩擦切换模型

(1)

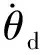
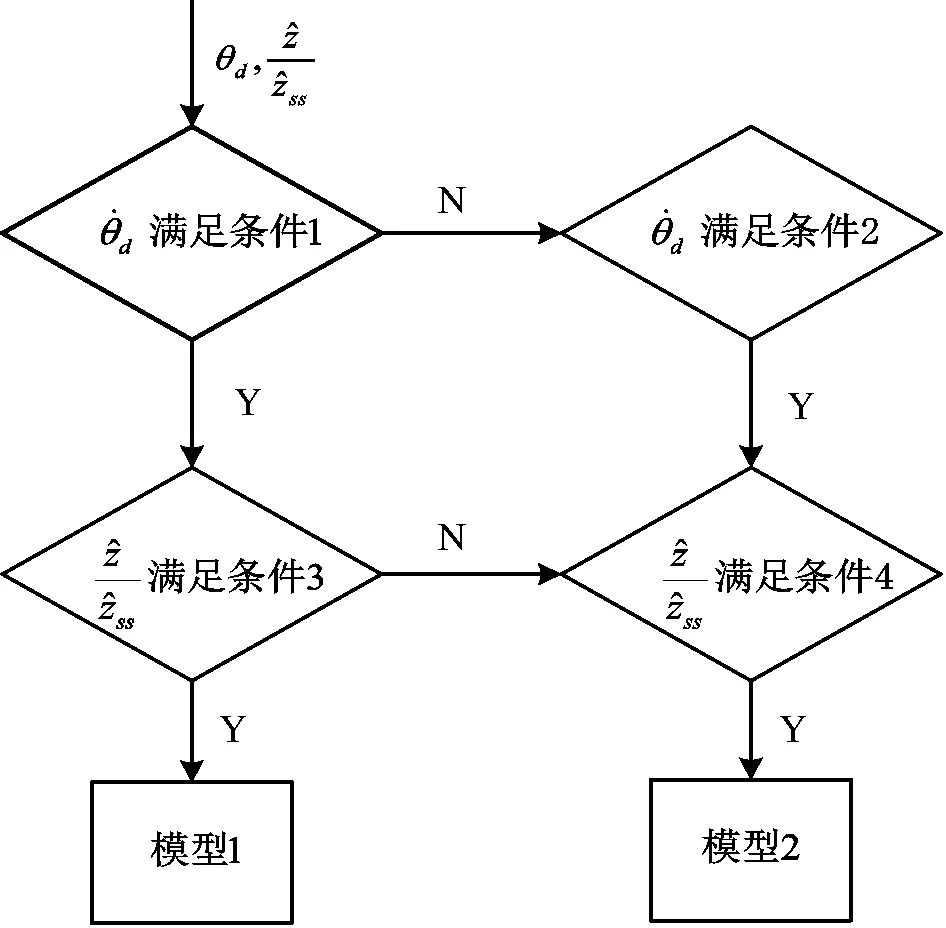
图2 摩擦切换条件流程图模型

1.2 LuGre摩擦模型

LuGre模型假定刚体表面是通过弹性刚鬃相接触，当刚体被外力作用进行相对位移时，刚鬃产生弹性形变，产生摩擦力，当刚鬃形变量达到最大时，物体便产生相对滑动，假设状态量 来表示相互接触面的刚鬃平均形变量，模型图如图3所示。

图3 摩擦力模型

伺服转台系统上的力矩关系可用下面的微分方程表示：

(2)

式(2)中Tfriction在LuGre模型中可表示如下：

基于文献计量学的国内人血白蛋白临床合理应用水平分析…………………………………………………… 黄晓倩等（19）：2688

(3)

(4)

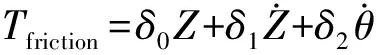
(5)

式中，δ0为刚鬃刚度系数，δ1为微观阻尼系数；Fc为库伦摩擦力矩，Fs为最大静摩擦力矩，vs为Stribeck角速度，Fc、Fs、vs、σ2为模型静态参数，σ0和σ1为模型动态参数。

Stribeck模型展示了速度与静摩擦力之间的函数关系:

(6)

2 参数辨识

模型的动静态参数由以下方法进行辨识:首先， 通过多组不同速度下的匀速运动实验数据，用遗传算法估算静态参数；然后，通过预滑动阶段的实验数据预估动态参数范围，再用遗传算法辨识动态参数[8]。本文以实验平台恒定转速[-1，1](rad/s)区间的电机正反向转动为例， 求得此转台模型的动静态参数。

2.1 静态参数辨识

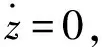
(7)

由式(2)可知，当转台转速保持恒定时，总摩擦力矩Tmotor与驱动力矩Tfriction相等。因此，转台伺服系统设定N组正反方向转速运动，可测得系统稳定状态下相应的驱动力矩Ti，由此得出转台转速与摩擦力矩的Stribeck曲线，如图4所示。

图4 转速与摩擦力矩的Stribeck曲线

(8)

设遗传算法中每一步迭代得到的辨识值为

(9)

(10)

取目标函数为

(11)

取N组转台伺服系统做匀速运动转速指令信号，根据参数搜索范围Fs∈[0，1]，Fc∈[0，0.1]，vs∈[0，0.1]，σ2∈[0，0.1]。使辨识目标Jm极小化，将实际的摩擦力矩值与通过遗传算法得到的摩擦力矩值作比较，最终得出在转速[-1，1] rad/s范围内电机正反转的动静态摩擦参数值，表1是辨识的参数值，因电机正反转状态不一样，得出的参数值会有略微差异。

表1 辨识的参数值

2.2 动态摩擦参数辨识

由于LuGre摩擦模型内部的不确定状态变量z不可直接测量，可在预滑动阶段按以下公式近似计算δ0，δ1的值：

(12)

(13)

J=0.5 kg·m2为转台的转动惯量，ΔFmotor和Δθ为总力矩和转台转角的变化量，由此可得σ0=252 Nm/s，σ1=4.6 N/m。

3 伺服转台系统的结构

转台伺服系统由上位机，STM32控制板，编码器，交流伺服电机等组成。系统以STM32控制板为核心，完成对控制信号的发送，干脉冲信号的采集，转台伺服系统平台的机械结构图如图5所示，转台伺服系统内部的伺服电机通过皮带与转台相连，通过控制伺服电机的旋转，带动转台的转动。实验转台采用闭环控制，该控制器采用PID转速反馈和摩擦补偿对位置环进行控制，伺服转台系统的控制方框图如图6所示。

图5 转台伺服系统机械结构图

图6 伺服转台系统的控制方框图

3.1 PID补偿设计

针对转速误差，本文使用PID反馈调节构成控制器：

(14)

式中，KP为比例增益，KI为积分增益，KD为微分增益，本文中的KP=50，KI=12，KD=5。

3.2 摩擦补偿

由以上分析得知伺服转台系统在刚启动和平稳运行两种工况下摩擦力的性质不同，并且在不同的工况下摩擦力的变化具有明确的特性。因此，可以假定在伺服转台系统整个运行的过程中可以由不同的摩擦模型来表征，针对这一事实，在已研究的LuGre模型的基础上，结合Stribeck模型和PID反馈调节建立基于切换摩擦模型理论的摩擦力辨识及补偿系统，对系统的摩擦力实时估计与补偿。

4 实验结果分析

基于上述的摩擦参数的辨识方法，获得伺服转台系统摩擦模型的参数，在得到的模型基础上利用PID反馈调节和摩擦补偿相结合的策略对摩擦造成的转速波动进行反馈补偿。

4.1 基于转台的Simulink仿真

在转台伺服系统中转台G(s)为被控对象，通过粒子群算法线性辨识程序对系统的输入输出进行辨识，得到系统的闭环传递函数，具体的参数式为

(15)

将含摩擦扰动的转速量作为反馈信号分别传递到摩擦补偿模块进行摩擦补偿和PID调节模块进行转速调节，从而做到系统速度的稳定控制。基于Simulink 建立的模拟上述伺服转台系统的仿真平台，其结构如图7所示。

图7 基于Simulink的伺服转台系统仿真平台

其中条件判断模块是由s函数编写，结构图如图8所示。

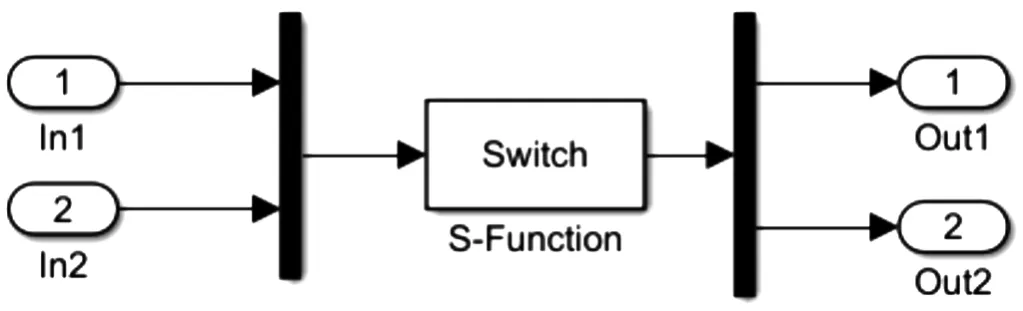
图8 条件判断模块子程序

4.2 实验结果分析

利用转台伺服系统仿真平台对正弦运动进行研究，运动的信号指令为y=sin(t)，未进行摩擦补偿时，得到如图9的转速和跟踪曲线进行摩擦补偿时得到如图10的转速和跟踪曲线，图11为补偿前后的误差跟踪曲线，图12为转台补偿前后的残差数据图。

图9 未进行补偿时的转速跟踪曲线

图10 补偿后的跟踪曲线

图11 跟踪误差曲线

图12 补偿前后的残差图

由图9和图10可知，当仿真平台未进行摩擦补偿时，转速在过零点左右会发生波动，速度跟踪会出现误差过大的情况，对摩擦补偿后，转台转速曲线在过零点的时候抖动现象明显减小。由图11可知，对摩擦进行补偿前后，系统的动态跟踪误差由最高的0.2817 rad/s降到了0.0741 rad/s，未加入补偿时的动态跟踪误差平均值约为0.01425 rad/s，而加上补偿之后速度跟踪误差平均值降低为0.00192 rad/s。同时本文对补偿前后的转速的残差值进行分析，如图11所示，在未进行摩擦补偿时，部分数据残差的置信区间不包含零点，说明部分实际数据与理论数据相差较大，会导致系统出现跟踪性能不高的问题，而经过摩擦补偿后的数据残差的置信区间均包含零点，说明实验数据能较好的符合理论数据。实验结果证明了基于切换理论建立的摩擦模型能全面精确地描述不同状态下的摩擦大小，基于该摩擦反馈补偿和PID调节的复合策略系统能提高系统的控制性能和跟踪性能。

5 结 论