考虑动态特性的模型参考自适应PMSM无位置传感器控制

朱瑞杰，陶春荣，杜仁慧，张 伟

(中国船舶重工集团公司第七二四研究所，南京 211106)

0 引 言

永磁同步电机矢量控制需要转子位置信息，传统方法通过在转子轴上安装旋转变压器等位置传感器来检测转子位置，而采用无位置传感器控制既可以应对恶劣环境(高低温、湿热等)，也能够有效降低系统成本。因此永磁同步电机无位置传感器控制的研究受到国内外学者的广泛关注[1-4]。

模型参考自适应法(Model Reference Adaptive System, MRAS)具有算法相对简单、稳态精度较高等优点，最早由C.Schauder于1989年用于异步电机转速辨识中[5]，之后又用于永磁同步电机无位置传感器控制。按照参考模型和可调模型选择的不同，主要有基于定子电流的MRAS方法[6-10]、基于定子磁链的MRAS方法[11-12]和基于无功功率的MRAS方法[13-14]。基于无功功率的方法从稳态方程出发，通过简化电机模型，使可调模型只与交轴电感有关，但其动态性能较差。文献[6-7]将电机自身作为参考模型，将估算的定子电流模型作为可调模型，实现了表贴式和内置式永磁同步电机的转子位置估算。文献[8]利用分段PI参数自适应调节器来实现永磁同步电机全转速范围无位置传感器控制，通过试凑的方法确定不同转速区域的PI参数，实验中稳态时角度观测误差可以达到10°以内，转速观测误差在5 r/min以内。文献[10]针对id=0的矢量控制，研究了一种只利用q轴电流进行无位置传感器控制的方法，并且利用调节时间来分析系统动态性能，但d轴、q轴电流都估算的模型参考自适应法更具有普遍意义。文献[11]将永磁同步电机的定子磁链方程作为参考模型，将估算的定子磁链模型作为可调模型，同时辨识转速和定子电阻，但文中没有对系统的动态性能进行理论分析。文献[12]以电压模型观测所得定子磁链作为参考模型，以电流模型观测所得定子磁链作为可调模型，利用根轨迹仅分析系统的稳定性。

已有文献中，采用基于模型参考自适应方法研究永磁同步电机无位置传感器控制时，大都只考虑稳态工况，一般不做动态分析。而电机在实际运行过程中，必然会有要求高动态响应的加速或减速运行状态。因此，研究模型参考自适应控制系统的动态特性至关重要。本文以文献[11]中基于定子磁链的参考模型和可调模型为基础，重点研究了控制系统的加减速动态特性。由于模型参考自适应系统是一个非线性系统，所以采用文献[15]中的小信号模型理论在稳态工作点附近对系统进行线性化处理，建立了小信号模型。在此基础上，利用劳斯稳定判据从理论上分析了系统的动态稳定性。结合稳态误差分析方法提出了一种自适应调节器PI参数计算方法，以适应不同的转速和转矩工况，仿真和实验结果表明，该方法能够实时准确估计电机的位置和转速状态，并且具有良好速度跟踪稳态精度和动态性能。

1 模型参考自适应转子位置估算

永磁同步电机在旋转坐标系下以定子磁链作为状态变量的数学模型为

(1)

式中，ud、uq分别为定子d、q轴电压；ψd、ψq分别为定子d、q轴磁链；Rs为定子相电阻；Ld、Lq分别为定子d、q轴电感；ψf为转子永磁体磁链；ωr为转子转速。

将式(1)用估计值的形式表示，得到可调模型为

(2)

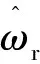
(3)

将式(3)简写如下：

(4)

根据式(4)建立状态方程为

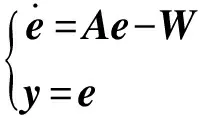
(5)

选择参考模型为

(6)

根据波波夫超稳定性理论，最终可得到转速估算表达式为[11]

(7)

(8)

转子位置角由转速积分得到

(9)

则整个MRAS无位置传感器矢量控制的结构框图，如图1所示。

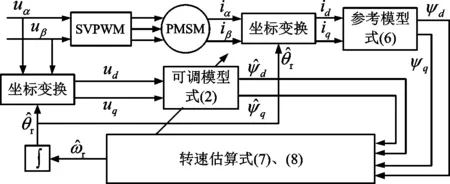
图1 MRAS无位置传感器矢量控制

2 系统动态特性分析

2.1 小信号模型

当电机实际转速由于外部干扰发生波动时，需要考虑估算转速的变化能否动态的跟踪实际转速的变化量。设永磁同步电机在稳态工作点的交直轴磁链和电压分别为ψd0、ψq0和ud0、uq0，电机转速为ωr0，则式(1)在稳态工作点的方程为

(10)

在稳态工作点施加小信号扰动，即

(11)

将式(11)代入式(1)得

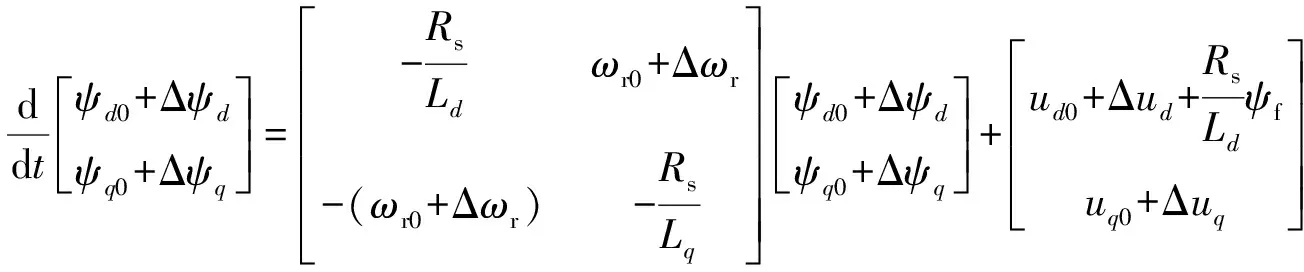
(12)

将式(12)减去式(10)，并忽略两个微小量的乘积，得到小信号状态方程为

(13)

同理，得到式(2)可调模型的小信号状态方程为

(14)

将式(11)代入(8)得

(15)

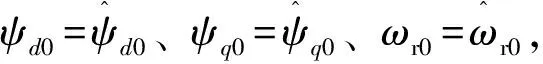
(16)

(17)

将式(13)、式(14)代入式(17)得

(18)

令

(19)

由式(16)和式(18)可得MRAS转速估算系统的小信号模型如图2所示。

图2 MRAS转速估算系统的小信号模型框图

2.2 小信号模型动态稳定性证明

根据图2可得系统闭环传递函数为

(20)

将式(19)代入式(20)，可得闭环特征方程为

D(s)=s3+a2s2+a1s+a0

(21)

式中

(22)

根据劳斯稳定判据，由特征方程(21)所表征的系统稳定的充分必要条件是劳斯表中的第一列各值为正。按劳斯稳定判据的要求，列出特征方程对应的劳斯表：

因为

(23)

所以

(24)

并且a2>0，a0>0，所以劳斯表中第一列系数为正，且与ψd0、ψq0、ωr0、Kp、Ki大小无关，说明转速估算系统在动态时也是稳定的，其估算转速的变化能够跟踪实际转速的变化。

2.3 自适应PI参数

根据波波夫超稳定性理论，式(5)和式(7)对应的误差系统结构框图[16]，如图3所示。

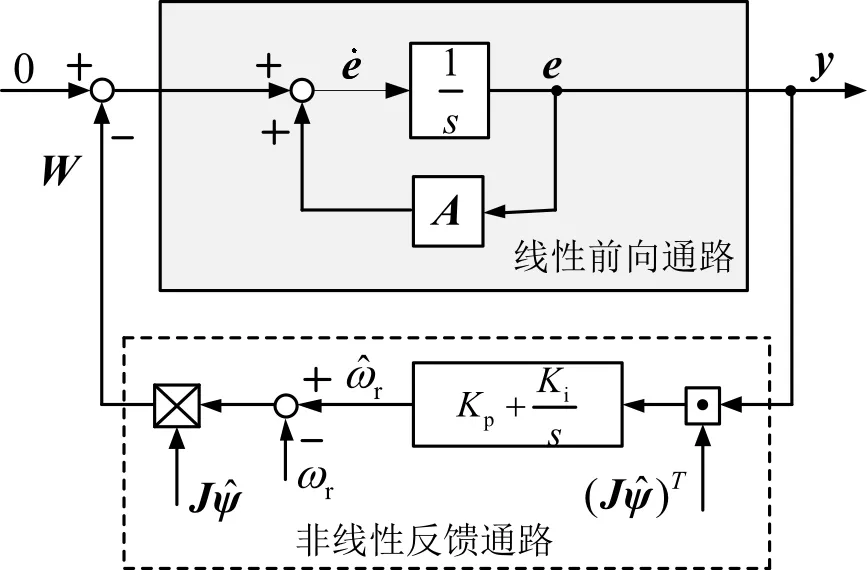
图3 误差系统结构框图

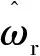
图4 转速估算误差系统结构框图

令

(25)

由图4可知，当加减速工况斜坡输入Rt作用时，转速稳态误差为

(26)

由式(26)可得

(27)

其中

(28)

理想情况下认为估算的磁链、转速与实际值相等，因此在选定转速稳态误差δ、加减速斜坡速率R的情况下，结合电机参数、交直轴电流、估算的电机转速由式(27)可以实时计算得到Ki。

传递函数H(s)的零点为

(29)

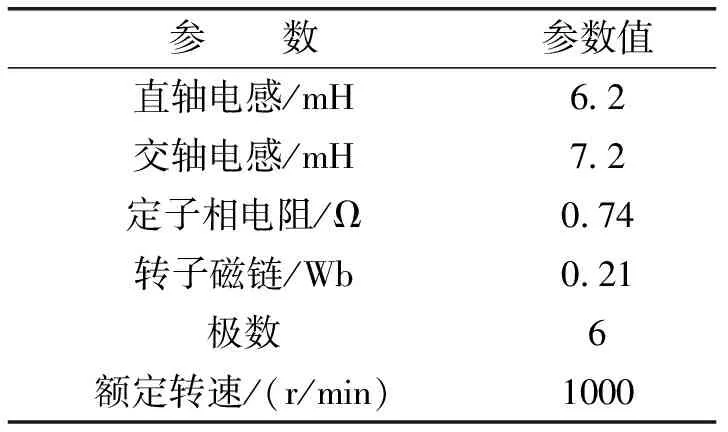
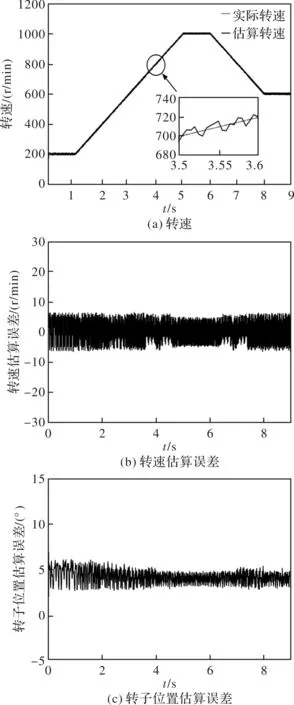
所以-Rs/Ld

(30)

为了得到较好的闭环根轨迹，Kp+Ki/s的零点-Ki/Kp应位于传递函数H(s)零点的左侧，且在开环极点的附近，同时为了确保电机的稳定性，Ki/Kp比例应足够大[17]，所以取Ki/Kp=Rs/Ld，由此计算得到Kp。

3 仿 真

采用Matlab/Simulink软件对无位置传感器控制方法进行仿真。电机参数如表1所示。仿真和下文实验都选取转速稳态误差δ=4 r/min，较快的加减速斜坡速率R为转速每秒加减200 r/min，来计算自适应PI参数(若实际工况加减速斜坡速率小于每秒加减200 r/min，则相当于可以得到更小的转速稳态误差δ)。仿真和下文实验中转子位置估算误差和转速估算误差都是估算的减去实际的。

表1 永磁同步电机参数

图5是电机按照转速每秒加减200 r/min，由1秒时的200 r/min恒加速到5秒时的1000 r/min，而后由6秒时的1000 r/min恒减速到8秒时的600 r/min，自适应PI参数、转速、转速估算误差、转子位置估算误差仿真波形，从图中可以看出估算转速始终能跟踪上实际转速，且加减速过程中误差基本在±4 r/min以内，满足自适应PI参数理论设计结果，另外转子位置估算误差也较小，在3°以内，速度较高时在零度附近波动。

图5 加减速过程仿真波形

4 实 验

为了验证理论分析和仿真结果，选用与表1中仿真电机参数相同的永磁同步电机进行实验。

图6为电机按照转速每秒加减200 r/min，由1秒时的200 r/min恒加速到5秒时的1000 r/min，而后由6秒时的1000 r/min恒减速到8秒时的600 r/min，图6(a)、图6(b)、图6(c)分别是相应的转速、转速估算误差、转子位置估算误差实验波形。从图6(a)、图6(b)中可以看出估算转速能较好的跟踪实际转速，加减速过程中误差基本在±6 r/min以内，相比于理论计算稍大一些，这主要是由于实验中逆变器死区等非理性因素影响造成的；图图6(c)中稳态和加减速过程中转子位置估算误差最大为6°。由此可见具有良好的动态性能。

图6 加减速过程实验波形

实验中由于逆变器死区等非理性因素影响，且这些因素较难完全补偿，导致转子位置估算误差不再是在零度附近波动，转速估算波动也比仿真时稍大，但比较文献[8]中的实验结果，误差尚在可接受范围内。

5 结 语

针对永磁同步电机实际工作过程中，不可避免面临加速、减速等工况，本文从理论上对动态性能进行了研究。用劳斯稳定判据证明了所建立小信号模型的动态稳定性，并提出一种自适应PI参数计算方法，通过仿真和实验验证了该方法的正确性，实现了无位置传感器控制方法良好的稳态和动态性能。