一种四足机器人伺服电机设计与优化
莫 为,莫会成,顾苗苗,李 红,郝 健,王洪彦3,,刘 康
(1.西安西微智能科技有限公司 西安 710077;2.陕西科技控股集团有限责任公司 西安 710077;3.陕西科控技术产业研究院有限公司 西安 710077)
0 引 言
永磁伺服电机是使用在各种机器人及高端工业智能装备中的核心功能部件,而高性能的永磁无刷力矩伺服电机是其中典型的代表之一。由于其控制策略灵活多样,响应速度快,转矩与功率密度大,有助于机器人做到轻量化并可节省出珍贵的空间[1-2]。随着机器人技术的飞速发展,对高性能永磁无刷力矩伺服电机的需求不断提升。四足机器人相较于工业用机器人、轮式、履带式机器人具有良好地人机协作性、运动灵活稳定、突出的环境适应性以及复杂地形机动能力,能帮助人类完成诸多危险性任务,在太空探索、巡逻、安防、救灾等甚至在军用领域有着极为广阔的应用前景[3-7]。
机器人用永磁无刷力矩伺服电机以其结构简单、性能优良、运行可靠性和维护性好以及整体性价比高获得了广泛的应用。但是,四足机器人用伺服电机相对于其他机器人用伺服电机又有所差别,譬如,在转矩波动、过载能力、转矩线性度和运行范围等方面,与其他机器人用伺服电机而言要求相对独特。本文针对某四足行走机器人的需求,优化设计了一款高转矩密度、低转矩波动、较好的转矩电流线性度永磁无刷力矩伺服电机,通过样机的使用,满足了四足机器人运行平稳,过载能力强、轻量化、宽范围运行等要求,获得了较好的效果,验证了设计的正确性,并进行了小批量试制。
1 性能指标与主要参数设计
1.1 电机性能指标
用于某四足机器人的一款永磁无刷力矩伺服电机的基本参数如表1所示,由于四足机器人结构独特,不仅有轻量化的要求,且可供安装的空间也十分有限,经结构优化设计后,采用空心无框结构,即电机仅由定子与空心转子组成,电机外径要求小于105 mm,电机总长不超过40 mm。为了简化控制,降低驱动控制成本,采取最为常见的id=0控制方式。

表1 电机基本指标要求
同时,还要求尽量保证输出转矩在0~16 N·m范围内要有较好的转矩电流线性度。从指标与要求可看出,该电机额定转矩密度为6 N·m/kg,功率密度是691 W/kg,预估反电势系数不大于34 V·kr/min,齿槽转矩小于额定转矩的1%,可见指标要求很严格,也就是说,一款电机要同时满足高的转矩密度、功率密度,较好的转矩电流线性度及转矩波动平稳度是很困难的。本文通过详细的理论分析,并借助有限元软件,利用其建模方便及强大的前、后处理能力,对影响电机性能的主要参数进行反复的充分的“场”与“路”综合分析与优化,使得解算结果更加精确,满足设计要求。
1.2 电机主要参数确定
一般情况下,电机的各参数满足下述关系:
(1)
式中,A为电机线负荷,Bδm1为气隙磁密基波幅值,P′为电机计算的功率值,n为电机转速,αi为计算极弧因数,Kdq1为基波电枢绕组系数,Lef为电枢铁心有效轴向长度,Dil为电枢铁心有效内径。
从式(1)可以看出,若要满足电机要求的指标,在有限的空间体积下,必须同时提高电机的线负荷A和气隙磁密基波幅值Bδm1,这样可以有效地提升转矩密度,但增加了铜耗,因此,综合电机的体积与长时半封闭自冷工作制,永磁体采用高性能的钕铁硼永磁材料,线负荷A不超过40 A/mm,由此可预估定子内径Dil为78 mm。
(1)槽极配合选取
永磁无刷力矩伺服电机的转速、转矩以及生产成本均与极数联系密切。极数少的电机成本比较低且更容易达到较高的转速,然而,定子和转子铁心轭部厚度与极对数pp成反比,定子齿宽度则与极对数pp成正比,假设电机空载气隙磁密相同,较高的极数使每极磁通降低,定转子铁心轭部厚度可以较薄,但定子齿的宽度将适当的变宽,这样就不会轻易地引起电机在加载特别是过载时的高磁密饱和,改善电机的力矩电流线性度[8-9]。
本设计要求在轻量化前提条件下转矩平稳性和转矩电流线性度要比较好,因此,适宜采用分数槽集中绕组槽极配合方式;由于齿槽转矩与转矩波动要小,因此极数尽可能取多,考虑到分数槽集中绕组槽极数比较接近,这样会造成每一时刻都会有磁通穿过气隙进入定子齿部但未进入定子轭部,没有形成有效的磁路闭合回路,产生无效激磁,因此,选取极数大于槽数的槽极配合方式,有助于弥补这一缺陷,提升电机的磁负荷;再次,采取多极多槽的极数大于槽数的配合方式,亦能增大电机转子旋转一周齿槽转矩变化的周期数,提高最低齿槽转矩阶数,进而从槽极配合的角度降低削弱齿槽转矩;最后,在满足线负荷和电流密度的基本要求下,尽量将电机定子铁心齿部的宽度适度加宽,定子铁心轭部厚度减薄,以降低电机过载时的高磁密饱和,从而达到转矩电流线性度较好的要求[10-11]。
(2)磁路结构与永磁磁极设计
永磁交流伺服电机一般有两种典型的磁路结构:永磁体贴于转子铁心表面的表贴式结构和嵌入转子铁心中内置式永磁结构。虽然内置式结构的转子凸极率可大于1,弱磁调速特性好,抗去磁能力也比较强,拥有磁阻转矩,但是内置永磁体结构整体漏磁系数大于表贴式结构,由于电机采用id=0控制,无弱磁调速要求,本方案选择表贴式永磁转子结构。
永磁磁极设计主要包括尺寸和材料型号选取,尺寸包含轴向长度、磁极宽度以及径向厚度,其中,转子轴向尺寸已确定,永磁体轴向长度与之保持一致,宽度与永磁体机械极弧系数相关,在永磁体粘接工艺和极间漏磁允许的情况下,尽量加大机械极弧系数,以增大有效磁通。厚度则与永磁体磁势相关,特别是不等厚度的永磁体结构,其最小厚度设计时更要以永磁体能够承受最高温度为前提条件,考虑永磁体的抗去磁能力,通常情况下,较高矫顽力钕铁硼永磁体最高工作温度在150℃左右,此时内禀退磁曲线和退磁曲线基本重合,电枢磁动势的大小决定永磁体厚度,若该温度所对应的矫顽力H′c为永磁体最大去磁点,对于分数槽集中绕组电机则电枢磁动势与永磁体磁势之间的关系如下:
(2)
式中,N为单线圈匝数,imax为最大电流,α为工艺参数,一般取0.7~0.97,hm即永磁体最大厚度,hmin为永磁体最小厚度,R为永磁体外圆半径,R1为永磁体内圆半径,bm为永磁体机械极弧系数对应的实际宽度,如图1所示。由于分数槽集中绕组电机槽极数比较接近,因而可近似看做单齿上绕制的线圈通入最大电流即是对应单极永磁体的最大去磁电枢磁动势,永磁体最小厚度hmin的基本设计只要符合上式即满足基本要求。
2 仿真分析与参数优化
针对该表贴式转子结构的永磁无刷力矩伺服电机,可采用优化永磁体厚度hm,从而增加气隙磁密和等效磁阻;优化偏心距h,实现不等气隙,进而优化空载气隙磁密,使定子齿部磁密分布均匀等,以达到减小电机齿槽转矩与转矩波动的目的。图1为表贴式永磁转子结构永磁磁极示意图,为便于永磁体粘接工艺实施以及降低加工成本,永磁体采用等宽设计,永磁体底圆紧贴转子空心轴R1,这样会造成极间气隙变大,等效极弧系数降低,总磁通量也随之下降,影响电机的力能指标,不能满足设计要求,因此需要对永磁磁极的h、hm、R1等参数借助有限元计算进行较为全面的仿真优化分析,最终确定其参数值。

图1 表贴式永磁磁极示意图
2.1 永磁体厚度的优化与选取
假设电机机械极弧系数不变,电机在1 r/min空载运行,通过仿真计算得出不同磁极厚度hm的齿槽转矩峰峰值;转速保持不变并输入额定电流,得到不同hm的额定转矩波峰与波谷值,代入式(3)得出转矩波动系数,将结果汇总如表2所示,由结果可知,齿槽转矩和转矩波动并不是随永磁体厚度hm的增大呈持续下降趋势,而是波动变化。
此外,将计算得出的空载气隙磁密Bmδ进行快速傅里叶变换,所得基波及各次谐波幅值分量代入式(4),再把电机转速调至1000 r/min空载运行,分别得出不同hm对空载气隙磁密谐波畸变率THDBmδ与线反电势基波幅值的影响,结果如图2所示,随hm的增加对谐波畸变率略有下降,反电势基波幅值有小幅提升。
(3)
式中,KTb为转矩波动系数,Tmax为实测最大转矩,Tmin为实测最小转矩。
(4)
式中,Bm1为气隙磁密基波幅值,Bmh为各阶次气隙磁密谐波分量。
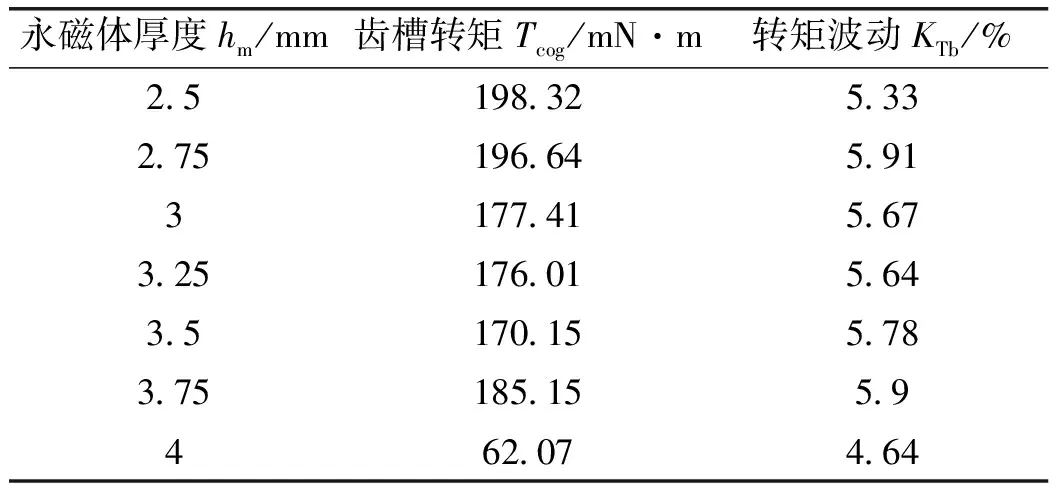
表2 永磁体厚度hm对齿槽转矩与转矩波动的影响

图2 谐波畸变率及反电势基波幅值随永磁体厚度hm的变化
2.2 偏心距的优化与选取
假定电机机械极弧系数与最小气隙不变,采用同样的仿真计算方法,对偏心距h影响齿槽转矩及转矩波动进行有限元仿真,结果如表3所示,可见,齿槽转矩随永磁体偏心距h增大逐渐减小到一定程度突然变大,而转矩波动则是随偏心距h的增大而减小。空载气隙磁密总谐波畸变率(THD%)与线反电势基波幅值随h变化如图3所示,由图可见,h的大小对谐波畸变率与反电势基波幅值有比较显著的影响。
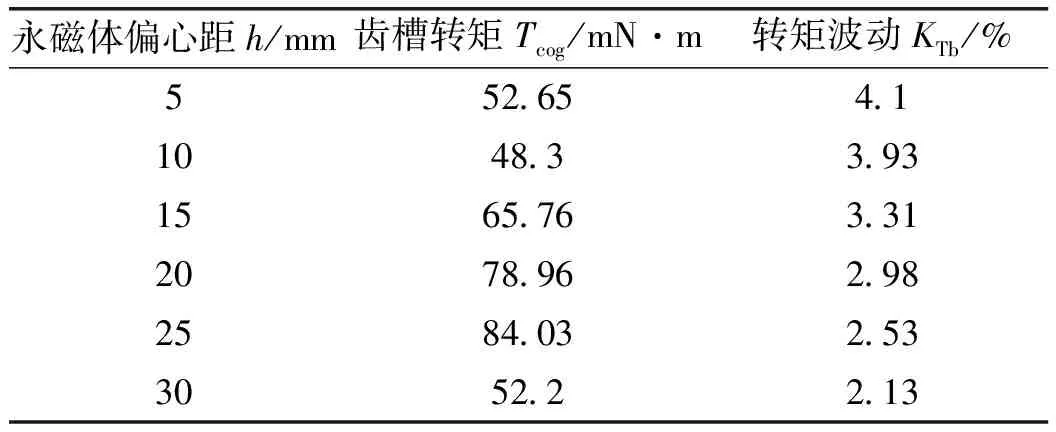
表3 永磁体偏心距h对齿槽转矩与转矩波动的影响
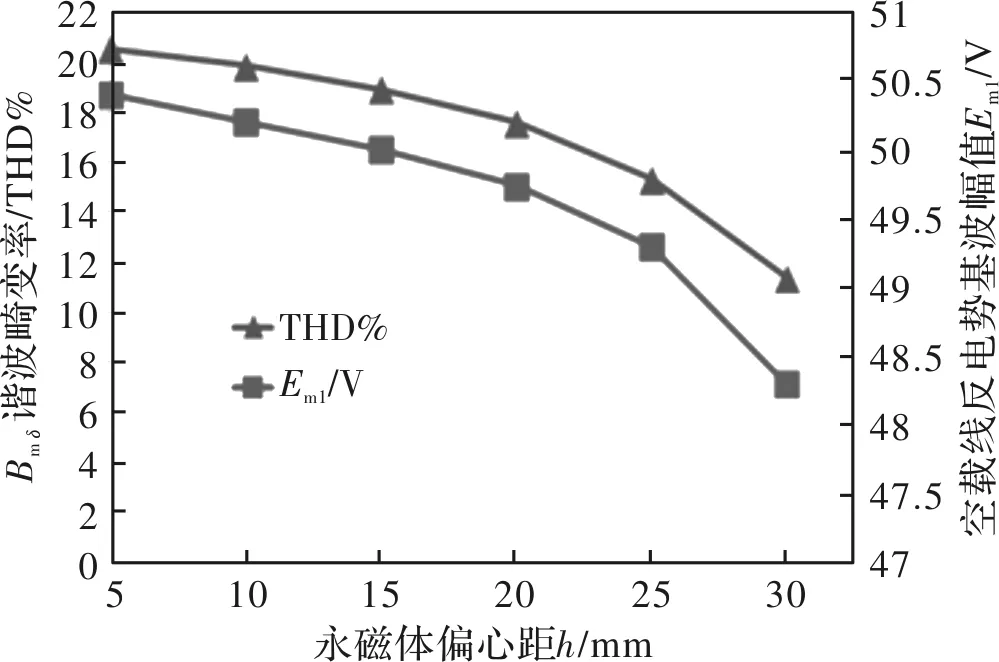
图3 不同永磁体h谐波畸变率分布
2.3 转矩电流线性度优化
影响电机转矩电流线性度的因素很多,电机铁心磁密饱和程度是重要的因素之一。通常情况下为使伺服电机性能做得更高,往往采用高性能冷轧无取向硅钢材料,冲片厚度一般为0.2、0.35 mm比较合适,根据厂商提供的数据,若两者的叠压系数均为0.95,则两种材料磁化曲线饱和点分别为1.71 T和1.68 T,也就是说当电机通入一定程度电流后定子铁心磁密会局部达到或超过该值,引起饱和,如再施加电流则转矩与电流不再呈线性关系,影响转矩与电流线性度。
电机以1 r/min转速运行,绕组通入2~38 A电流,永磁体厚度hm分别为2.5 mm和4 mm时,仿真计算电机输出转矩值与理想转矩电流曲线如图4所示,由图可知,当转矩接近2倍额定转矩时,转矩电流线性度出现非线性,电流越大线性度越差,同时,永磁体厚度越小线性度越差,电机所能输出的转矩越小。为进一步说明电流对电机定子铁心磁场饱和程度的影响,通过电机Maxwell 2D有限元模型,对比空载运行和输入38 A电流时的磁密分布云图,如图5(a)与图5(b)所示,可以看出电机齿部磁密由空载时约1.47 T增长至1.77 T,电枢反应增磁效果明显,铁心已处于饱和状态,此时从图4也可以看出,对应的转矩与理想输出转矩的差距十分显著,因此,当电机在非弱磁状态下运行,电枢反应增磁对电机输出转矩有抑制作用。
运用同样的方法,也可分析计算出永磁体偏心距h对转矩电流线性度影响,偏心距h为15 mm和30 mm时,电机输出转矩与理想转矩输出比较如图6所示。
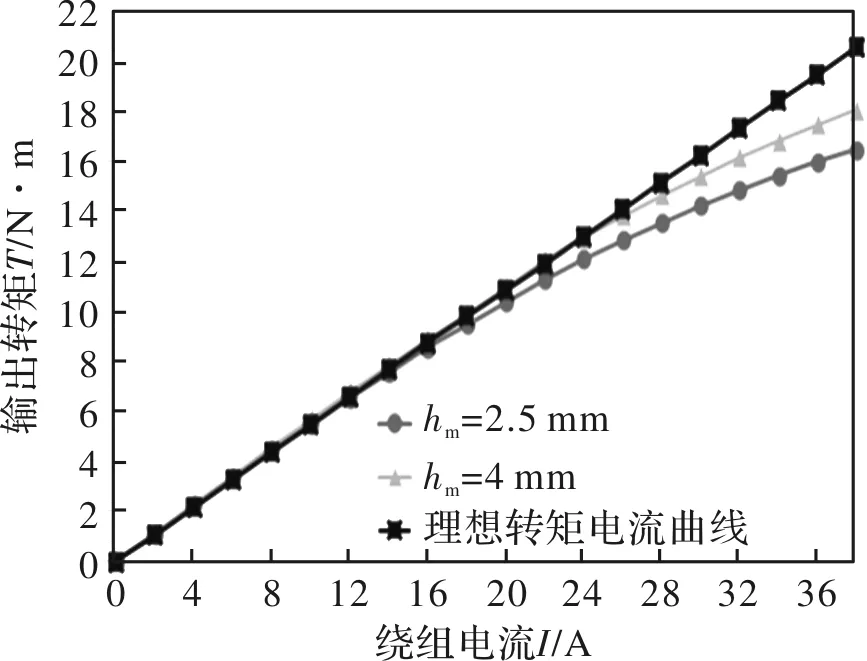
图4 不同永磁体厚度hm转矩电流曲线

图5 空载与满载运行磁密分布云图
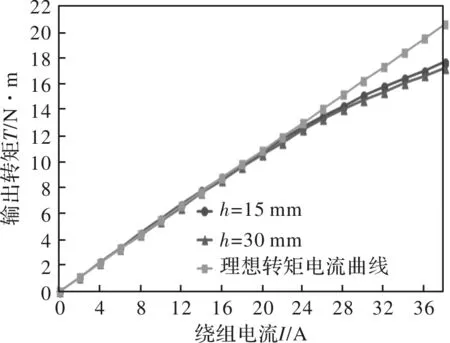
图6 不同永磁体偏心距h转矩电流曲线
通过以上对于永磁体厚度hm和偏心距h的设计与优化,并根据实际需求具体分析计算,综合考虑各种因素,本设计方案中选取相应的永磁体厚度hm与偏心距h。
3 试验验证
根据上述分析与设计优化,加工和制造样机如图7所示。图中机壳、端盖、转轴均为试验用工艺装备。

图7 永磁无刷力矩伺服电机样机实物图
系统性能测试平台及实验环境如图8所示,测试平台主要由美国Magtrol测功机、日本横河高精度功率分析仪、以色列埃莫DOUBLE Gold-Twitter 140 A/80 V伺服驱动器、示波器、电脑、激光测速器、电流钳等构成。齿槽转矩与转矩波动采用专用测试平台。

图8 系统测试平台及实验环境
测试1000 r/min转速下的线反电势幅值为48.8 V,波形如图9所示,可以看出,波形正弦度高波形平滑,基本满足要求。再将直流母线电压UDC调至74 V,上位机给定2 A的直流母线电流IDC, 通过激光测速器测得空载最高转速为1480 r/min,符合大于1400 r/min的技术要求。
齿槽转矩与转矩波动测试:将电机调至1 r/min,旋转一圈测得电机齿槽转矩如图10所示,最大转矩为0.0281 N·m,最小为-0.0256 N·m,峰峰值0.0537 N·m,单峰最大值约为额定转矩的0.47%,峰峰值约为额定转矩的0.9%,小于要求值1%,满足设计要求。
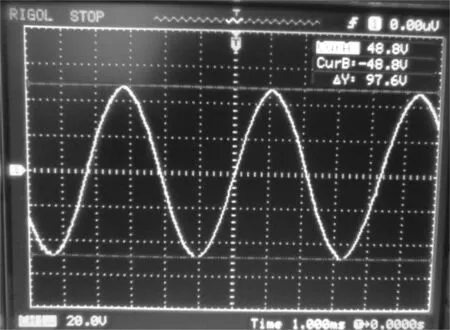
图9 实测空载反电势波形

图10 实测齿槽转矩波形
将电机转速调至1 r/min,转矩为6 Nm,旋转一圈测得电机输出最大转矩6.4861 Nm,最小为6.0742 N·m,波形如图11所示,转矩波动约为3.28%,小于5%的要求,满足设计要求。
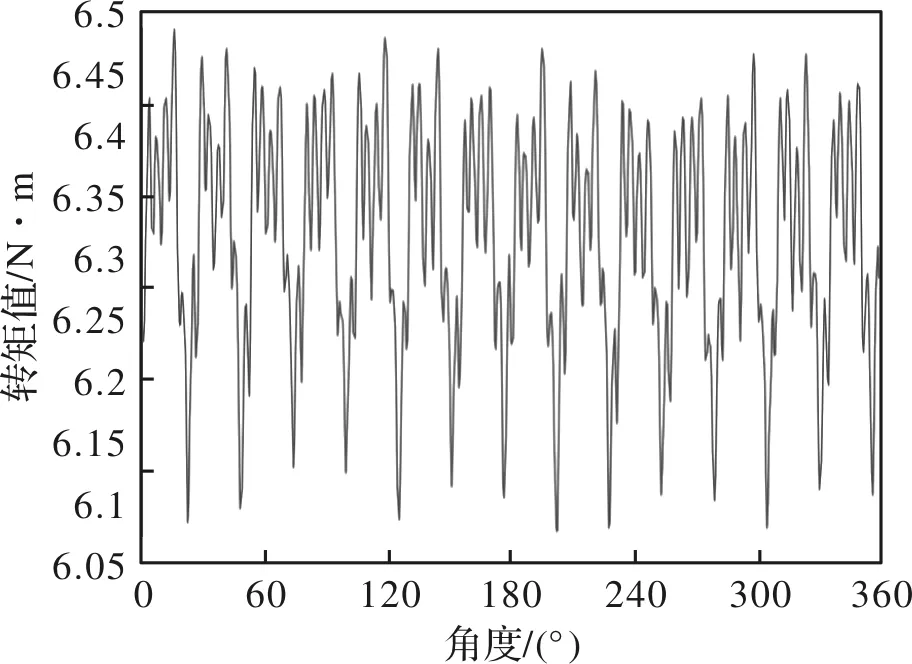
图11 实测转矩波动波形
转矩电流线性度测试:通过上位机转速设置为0 r/min,给定驱动器5~65 A不等的堵转直流母线电流IDC,得出在没有转速、铁耗及风摩擦损耗影响下的电机转矩输出,实测数据与对应的理想曲线以及仿真计算值如图12所示,仿真计算与实测数据基本一致,证明仿真计算方法合理,能够为设计提供可靠的参考,当直流母线电流大于45 A时,电机转矩电流线性度逐渐变差,但在直流母线电流为55 A时测得转矩输出16.47 N·m,基本满足输出转矩在16 N·m范围内转矩电流线性度要比较好的要求。

图12 转矩电流曲线
4 结 论
本文针对某型号四足机器人用永磁无刷力伺服电机,通过理论分析与有限元仿真,优化设计了一款高功率密度、高转矩密度、转矩脉动平稳且拥有较好的转矩电流线性度的永磁无刷力矩伺服电机。得出以下几点结论:
(1)采用多极多槽的分数槽集中绕组,且极数多于槽数的槽极比设计,既能提高气隙磁密,又能够适度增大齿宽,减小定子轭部尺寸,有效降低定子齿磁密,提高转矩电流线性度。
(2)对于等宽的永磁磁极结构,改变永磁体厚度与偏心距能够改善电机的齿槽转矩与转矩波动,但齿槽转矩与转矩波动并不是随着永磁体厚度与偏心距的减小而降低,而是波动变化,要通过详细的优化计算选取。
(3)空载反电势随着永磁体厚度的增加而增大,但对于削减气隙磁密谐波畸变率帮助有限。
(4)永磁体偏心距增大会减小空载反电势,但对于削减气隙磁密谐波畸变率很有帮助。

