水雷目标探测攻击指令正确性评判方法研究

倪世丰，龙小民，陈 川

（1.海装驻宜昌地区军事代表室；2.中国船舶重工集团有限公司第七一〇研究所，湖北 宜昌 443003）

0 引言

主动攻击水雷是一种战斗部主动航行接近目标，并对其实施攻击的水雷[1]。水雷目标探测系统实现对舰艇目标的探测、识别、定位、目标运动特性参数估计和最佳攻击点预测，当确认目标进入打击范围时，适时输出攻击指令，并将估计的攻击点位置参数传递给战斗部，战斗部航行到该位置并实施攻击。本文针对目标探测攻击指令输出是否正确的试验评判方法进行研究，提出了一种基于向量表达式的试验评判方法，逻辑简单易懂，且易于软件实现。

1 评判准则

对于定向攻击水雷，目标探测攻击指令输出是否正确的评判准则为：将目标探测系统输出攻击指令的时刻作为起始时刻，考虑水雷战斗部上浮时间，得到水雷战斗部到达估计攻击点的时刻。该时刻目标舰艇（作为体积目标）到估计攻击点的最小距离应小于误差要求。

2 数学模型需考虑的因素

对于利用舰船声场的水雷目标探测系统，一般是将目标舰艇作为点目标声源进行处理[2]，以舰艇的声中心位置为基础建立数学解算模型。而在进行试验数据处理时，通常将舰艇作为体积目标[3-6]，即有长度和宽度；且水雷试验时一般通过卫星定位设备测量目标舰艇通过时的航迹，卫星定位设备安装于舰艇的某一位置。因此，评判目标探测攻击指令输出是否正确时，需要综合考虑船长、船宽、卫星定位设备安装位置、目标探测攻击点估计位置等多个因素，统一建立数学模型。根据以上分析，本文建立了2种数学模型[7-8]，分别为模型Ⅰ（假设舰艇为线目标，即只考虑船长，不考虑船宽）和模型Ⅱ（假设舰艇为体积目标，即同时考虑船长和船宽）；并给出了 2种数学模型下，评价目标探测攻击指令输出是否正确的计算方法。

3 数学模型Ⅰ

假设舰艇为线目标，即只考虑船长，不考虑船宽；水雷在水面投影为O’点；GPS天线安装于船上G点，G点距离船首A点的长度为ds，距离船尾B点的长度为dw；估计的攻击点位于O点，O点到G点、A点和B点的距离分别为d、d1和d2；船的航向角为α。据此条件，在平面坐标系中绘出的几何态势如图1所示。图中舰艇坐标为从输出攻击指令开始，经过水雷战斗部航行至估计攻击点的时间后，GPS记录的舰艇所在位置。

设A点、B点、G点、O点和O’点的坐标分别为A（xA，yA）、B（xB，yB）、G（xG，yG）、O（xO，yO） 和O（0，0）。

G点坐标通过 GPS记录的目标航路数据获取经纬度，然后结合水雷二次定位后的经纬度转换到XY坐标；O点坐标通过解析内记数据中的估计攻击点获取；A点和B点坐标可由下式求得：

舰艇通过航路所在直线可用下式表示：

由点到直线的距离公式可知，攻击点O到该直线的距离可表示为

式（3）中，为便于表示，记k=tanα。

考虑舰艇不是一个无限长的目标，所以按照式（3）计算出的攻击点到航路所在直线的距离不一定是攻击点到舰艇的最近距离，应分以下 3种情况讨论。

首先引入以下向量，分别记作：

1）情况1：若攻击点O在船首方向，位置关系如图2所示。此时 ∠OAB＞ 90°，且 ∠OBA＜ 90°，可采用向量表示为

此时，攻击点到舰艇的最小距离d为

若d≤攻击点估计误差指标要求，则判定攻击指令输出正确。

图2 攻击点在船首方向的位置关系示意图Fig.2 Schematic diagram of position relation of attack point in bow direction

2）情况2：若攻击点O在船尾方向，位置关系如图3所示。此时 ∠OAB＜ 90°，且 ∠OBA＞ 90°，即：

此时，攻击点到舰艇的最小距离d：

若d≤攻击点估计误差指标要求，则判定攻击指令输出正确。

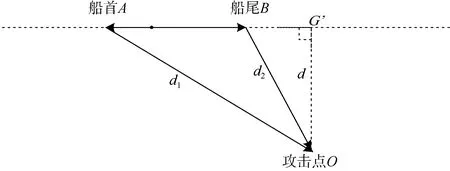
图3 攻击点在船尾方向的位置关系示意图Fig.3 Schematic diagram of position relation of attack point in aft direction

3）情况 3：若攻击点在舰艇正横方向，位置关系图如图4所示。 此时 ∠OAB＜ 90°且∠OBA＜ 90°，即：

此时，攻击点到舰艇的最小距离d为

若d≤攻击点估计误差指标要求，则判定攻击指令输出正确。

设攻击点到舰艇距离最近的点为G’，记AG’=d0，此时有：

结合A点的坐标和舰船航向α可知G’的坐标为

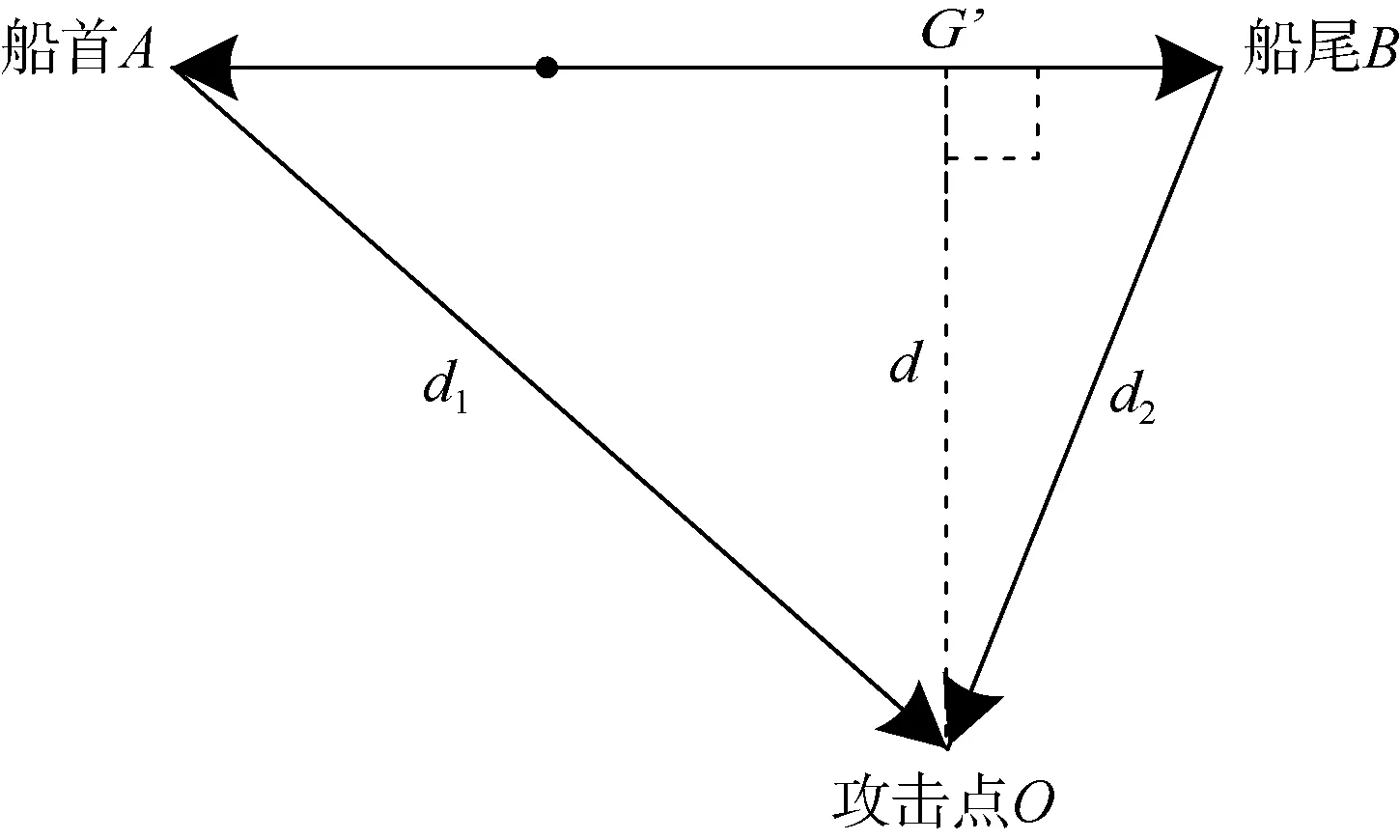
图4 攻击点在船正横方向的位置关系示意图Fig.4 Schematic diagram of position relation of attack point in abeam direction

4 数学模型Ⅱ

假设船为体积目标，即既有长度，又有宽度；GPS安装于船上G点，G点到左舷的距离为dL，到船尾的距离为dW；设船长L，船宽为W。根据此条件，在平面坐标系中绘出的几何态势如图 5所示。

根据船的航向和前面所给出的同船舷的相对位置关系，我们可以给出船首AR点、船首AL点、船尾BR点和船尾BL点的坐标值。记船首到的距离为ds=L-dw，到船右舷的距离为dR=W-dL：

图5 几何示意图（面目标）Fig.5 Geometric schematic diagram（area target）

由式（1）可知，其中：

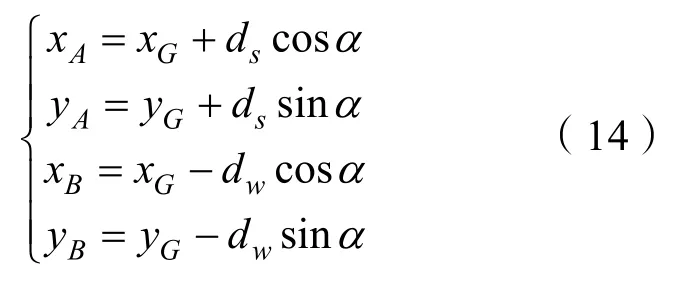
由船角上 4点和攻击点位置重新绘制位置关系图，如图6所示。

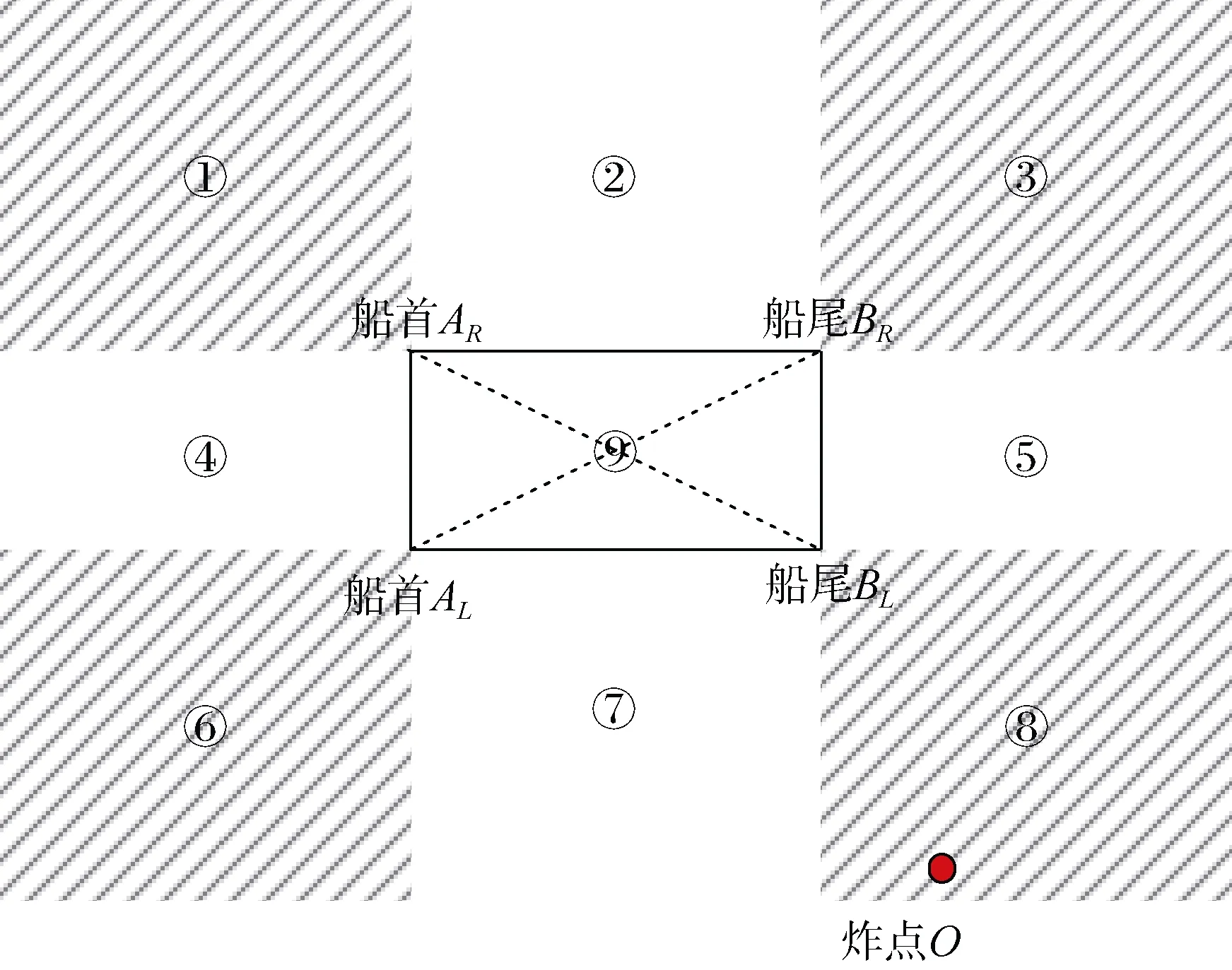
图6 位置关系示意图（面目标）Fig.6 Schematic diagram of position relation（area target）

当攻击点分布在阴影区域内时，最近距离由攻击点到船角上4点的距离决定；当攻击点分布在船身内时（即图中⑨号区域），默认最近距离为 0；当攻击点分布在空白区域内时，最近距离由攻击点到对应线段所在直线的距离决定。

由船角上4个点所确定的4条直线分别为

按照之前的分析，将求舰艇离攻击点最小距离的过程分为3类情况。

1）第1类，攻击点位于阴影区。

2）第2类，攻击点位于船身内，此时判决成立的条件为

3）第3类，攻击点位于空白区。

5 结束语

本文建立了考虑舰艇为线目标和体积目标时的2种数学模型，并给出了相应数学模型下目标探测攻击指令输出是否正确的评判方法，该成果可直接应用于水雷研制。一般情况下，为了简化数据处理流程采用模型Ⅰ，根据水雷研制和试验数据处理的需要也可选用模型Ⅱ。