悬停空投鱼雷攻击水下目标投雷点计算方法

刘建兵

（中国人民解放军 91439部队43分队，辽宁 大连 116041）

0 引言

舰载直升机反潜是水面舰艇对抗潜艇的方法之一。由于水文气象等客观因素对舰载机搜攻潜有较大影响，在水面舰艇突然受到较大威胁时，舰载机就不可能按部就班地完成搜攻潜的全过程[1]，而敌潜艇很可能已经发现吊放声呐主动探测信号并进行规避机动[2]。吊放声呐只能测定敌潜艇相对位置，舰载机在敌潜艇信息不完整的情况下，选择悬停空投鱼雷是最为快速、行之有效的攻击手段。

直升机悬停空投鱼雷攻击水下目标特点是，鱼雷水下搜索目标范围大、攻击目标距离较远、精确打击目标能力强。直升机悬停投雷的基本条件为逆风悬停，速度为0[3]，鱼雷入水后的初始航向与直升机航向一致。在悬停投雷时，如何确定投雷点位置是非常关键的问题。在目标距离一定的情况下，如果鱼雷搜索的主航向不能对准目标或方位偏差过大，鱼雷就可能捕获不到目标，从而失去精确打击目标能力。为使鱼雷入水后其主航向能够基本对准目标，投雷前必须计算确定出直升机悬停投雷点位置，以实现准确打击水下目标。

1 直升机悬停投雷条件和基本假设

1.1 投雷条件[4]

假设的投雷条件如下：投放方式为悬停（0 km/h），直升机航向误差为±3°，鱼雷攻击方式为蛇行搜索攻击水下目标。

1.2 确定投雷点的基本假设

假定直升机投雷点的正投影与鱼雷的入水点相一致，假定鱼雷入水时刻其初始航向与直升机投雷时刻的航向保持一致，假定从鱼雷挂机到投雷结束时的风向是不变的[5]。

2 直升机悬停投雷点的确定

2.1 基本参数的确定

1）鱼雷的主航向角是已知的，设主航向角为ωi。以下列 4 个主航向为例：ωi＝-95°，+120°，-150°，180°。

2）投雷海区的风向可由风向仪测出，设风向角为α。

3）设直升机投雷时航向为β，根据测出的投雷海区风向（风向角为α），则

4）设鱼雷入水后蛇形搜索的基准航向为Ki，则Ki=β+ωi,即:

5）设鱼雷入水点与目标的距离为D=1 500 m。

6）目标的大地坐标W（λO,ψO）或W（XO,YO）作为已知量由 GPS测定；设直升机投雷点的坐标为P（λi,ψi）或P（Xi,Yi），则P点的坐标或位置就是投雷前需要我们解算的未知量。

2.2 用高斯投影法求取投雷点坐标

在目标距离D确定的情况下，投雷点必然落在以目标为圆心以D为半径的圆上，如图1所示。

在高斯坐标系中，目标和鱼雷入水点必然位于某一度带的高斯平面直角坐标系中，如图2所示，我们可在高斯平面直角坐标系中建立方程组，求解投雷点的精确坐标值。

图1 投雷点坐标圆Fig.1 Coordinate circle of torpedo release point

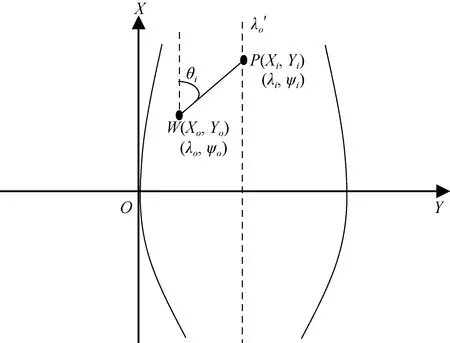
图2 目标和投雷点的高斯坐标投影Fig.2 Gauss coordinate projection of target and torpedo release point

设投雷点的平面方位角为θi，根据大地测量学的高斯投影法[6]，则其大地方位角为

式中：Rw为W点的子午线收敛角；λw为目标的经度值；λO′为所处度带的中央子午线值；φw为目标的纬度值。当目标位于中央子午线以东时，Rw取正值，反之为负值。

在高斯平面直角坐标系中

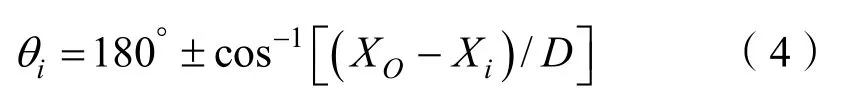
将式（4）代入式（3），解得：

由于鱼雷的基准航向角Ki与iθ地的差值为180°，因此：

将式（6）代入式（2），解得:

而P点相对W点的圆方程为

将式（7）与式（8）联立得方程组

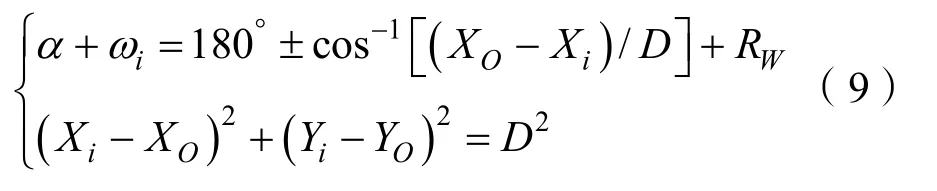
解得：

从式（10）中可以看出，在风向、鱼雷主行向和目标距离一定的情况下，有唯一的一个坐标点满足精确打击投雷条件，这个点就是精确求解的投雷点。

2.3 用欧氏几何法分析投雷点的位置

在投雷范围不大时，可以将投雷区域完全看作几何平面。因此也可在欧氏几何平面上[7]来分析投雷点的坐标位置，如图3所示。

以目标为原点，以正北方向为X轴建立平面直角坐标系XOY；以目标为圆心，以目标距离D为半径作圆。OA为风向，其反向延长线OB为直升机悬停投雷航向；OB旋转ωi角得OC为鱼雷主航向，则OC的反向延长线交圆于P点。

从图中可以看出，P点就是我们所确定的投雷点位置。其平面直角坐标为

图3 欧氏几何平面分析图Fig.3 Euclidean geometric plane analysis diagram

如果将投雷点用极坐标来表示，则为

式中：θi为投雷点相对目标的方位角；ρ为目标距。从式（11）、（12）中可以看出，鱼雷主航向ωi确定了，并测出投雷前风向角α，投雷点的坐标位置即可确定。

据上述，假设投雷海区几种风向（风向角为α），目标距D=1 500 m，计算确定投雷点相对目标方位角和目标相对投雷点方位角的数据见表1（注：α+ωi和β+ωi分别是投雷浮标相对目标的方位角和目标相对浮标的方位角）。

表1 投雷点相对目标方位角和目标相对投雷点方位角的数据Table 1 Azimuth date of torpedo release point relative to target and target relative to torpedo release point

表1（续）

3 结束语

本文对悬停空投鱼雷攻击水下目标投雷点计算方法进行了研究分析，比较2种方法可以看出，欧氏几何法比较简单直观，在实施过程中快速方便。在只使用本舰具有的测距仪、风向仪、船用罗经、分罗经和方位仪情况下，可快捷地测出有关参数值，并计算确定投雷点坐标位置。高斯投影法考虑了大地收敛角，其计算确定投雷点坐标精度较高，但在使用本舰设备基础上，仍需2台差分GPS和数据处理等外协设备，一定程度上加大了投入。因此，在误差许可的范围内采用欧氏几何法确定投雷点坐标是较为理想的方法。

在某型空投鱼雷试验中，采用欧氏几何法确定投雷点，被试鱼雷均准确命中目标。研究结果表明，此方法应用快捷有效，且投入少，可为部队投雷作战使用、训练提供决策理论指导，对提高直升机反潜[8]能力具有现实意义。