水下拖体姿态角自适应控制器设计

井安言，裴武波

（中国船舶重工集团有限公司 第七一〇研究所，湖北 宜昌 443003）

0 引言

相比于陆地，海洋对人类来说要陌生许多，受制于种种因素，人类对于海洋知之甚少。近年来，水下探测设备的发展受到了广泛关注，水下拖曳系统就是其中之一。水下拖曳系统由母船，拖缆和拖体组成，母船与拖体通过拖缆相连，母船可以是水面船舶或半潜式航行体等常规动力航行器。在水下拖曳系统的控制技术研究中，水下拖体的姿态角控制一直是阻碍其技术发展的瓶颈问题。

当前水下拖体姿态角控制的难点在于：1）水下洋流不稳定，导致拖体受到不规则扰动；2）母船受海面波浪的影响通过拖缆传递到拖体上，导致拖曳力处于不规则时变状态，干扰拖体的水下姿态；3）拖缆受不规则洋流影响，传递到拖体上导致拖体的工作姿态受到干扰。针对以上难点，国内外学者进行了大量研究，并取得了一些成果[1-10]。加拿大的Buckham B[1]小组在2003年针对带拖体的半潜式航行器整体采用集总质量估计方法进行建模并设计了PID控制器进行控制。日本的Asuma Minowa和Masayoshi Toda[2]在2015年进行了关于水下拖曳航行器（TUV）鲁棒控制的预研课题，提出了一种基于高增益观测器的TUV鲁棒运动控制器。之后 Asuma Minowa和 Masayoshi Toda[3]在2018年根据前期预研，针对高阶系统进行进一步研究，提出了一种基于 LQI（linear-quadraticintegral）的控制器。此外，还有日本的Naomi Kato等人[4-5]研究了关于水下拖曳航行器的模糊控制器设计，在垂直方向和水平方向耦合模型下提出了一种模糊控制规则。葡萄牙的 F.C.Teixeira等人[6-7]分别在2006年、2010年设计了一种非线性自适应控制器并且通过仿真展示该控制器运用在二体拖曳模型上的优异性能。Woolsey和Gargett[8]提出通过人为改变拖体的重心位置，改变其定深翼板的攻角，来达到控制拖体定深的目的。上海交通大学的王飞[9]提出了一种嵌套二分法求解水下拖曳系统模型的数值解，并设计了一种模糊PID控制器解决拖缆的定深问题，计算机仿真显示了其良好的性能。

本文将根据 Masayoshi Toda[10]提出的水下拖曳系统的动力学模型，设计一种神经网络自适应控制器，通过神经网络在线学习逼近模型中的非线性不确定项，起到补偿不规则干扰以及保护模型非线性特性的作用，通过计算机仿真验证该控制器对于水下拖体俯仰角控制的有效性。

1 水下拖曳系统运动建模

1.1 坐标系表示

为了研究方便，也因为拖体在垂直面上的运动控制是最重要的，所以只考虑拖体在垂直面上的运动。除了将模型的运动限制在二维垂直面上以外，还有如下假设：1）母船以恒定速度v0作匀速直线运动；2）忽略关于母船的动力学问题；3）环境干扰不作考虑（包括洋流与波浪）；4）拖缆视为一个刚性单元，其质量集中于末点；5）所有作用于拖缆单元的力均视为作用于其质点；6）拖体的深度与姿态角可测。

坐标系O0X0Z0的原点O0在拖缆与母船的连接点上，坐标系O1X1Z1的原点O1在拖缆与拖体的连接点上，且O1为拖缆的质心，坐标系O2X2Z2的原点O2在拖体的中心，q1表示拖缆与水平面的夹角，q2表示拖体的攻角，规定逆时针方向为所有角度的正方向。

坐标表示如图1所示。

图1 模型的坐标表示Fig.1 Coordinate representation of model

1.2 水下拖曳系统动力学模型

使用集总质量估计法建模如下：

水下拖曳系统模型有以下2个特性：

水下拖曳系统模型式（1）可以改写为

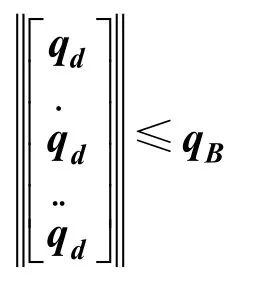
如果f（·）和E-1精确已知，那么PD控制律可以设计为

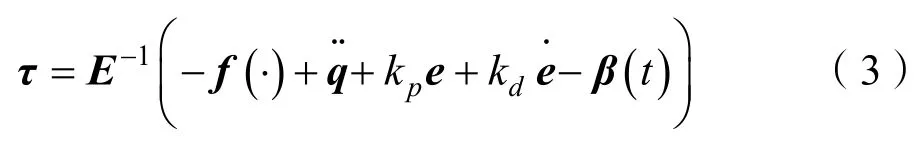
式中：kp、kd分别为位置和速度增益矩阵；β（t）是关于目标攻角跟踪误差的辅助输入，定义当辅助输入为 0时，将控制律式（3）应用于式（2），可得系统的跟踪误差渐进稳定。但是实际工程应用中f（·）和E-1不可能精确已知，所以需要其他的控制方法与控制算法。

2 神经网络自适应控制器设计

2.1 问题的提出

设跟踪误差为

定义跟踪误差函数为

将跟踪误差函数对时间的导数代入式（1），将水下拖曳系统动力学方程写作关于跟踪误差函数的表达式，如下：

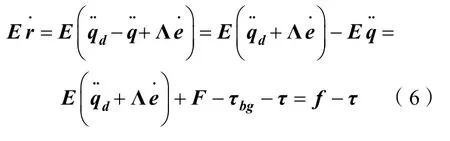
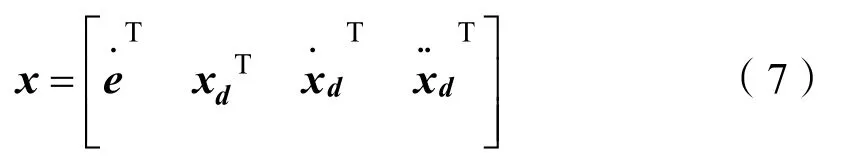
定义控制律为

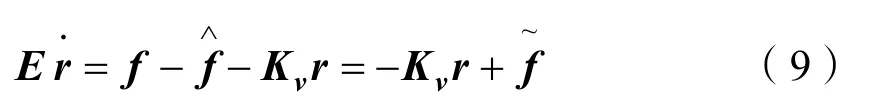
至此已经搭建了一个完整的误差系统，式中跟踪误差函数受到函数逼近误差的影响。控制输入τ包含一个比例-微分（PD）项利用 Lyapunov定理分析系统稳定性，定义Lyapunov函数为

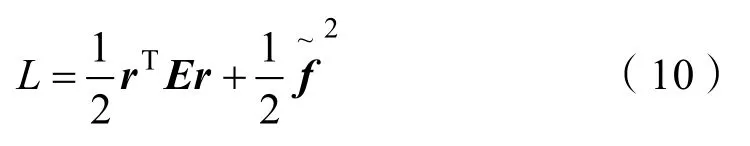
对L求一阶导，得

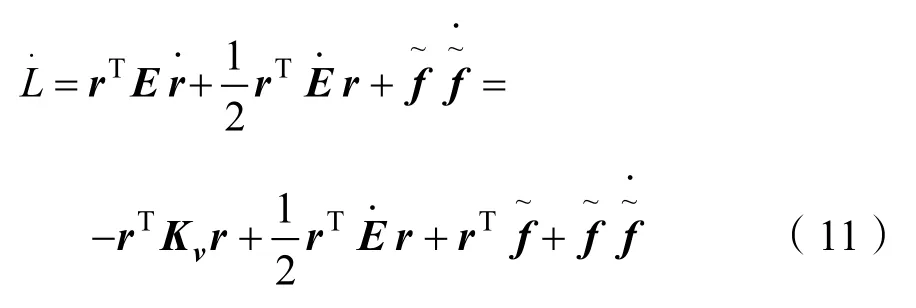
根据水下拖曳系统模型的特性可知，E为斜对称矩阵，即对任意向量s，有化简式（11）得

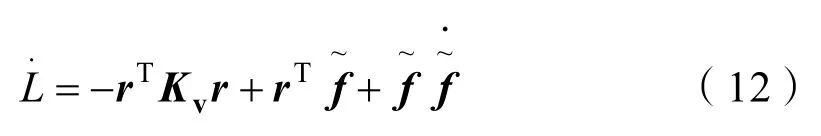
由式（12）分析可知，当Kv固定的情况下，控制系统的稳定性取决于神经网络逼近函数f的精度。

2.2 针对函数f（x）逼近的控制

2.2.1 控制器的设计

本文选择径向基函数（RBF）神经网络作为对函数f（x）进行逼近的神经网络。径向基函数神经网络是一个只有2层的网络，在网络的中间层，即隐藏层，它以对局部相应的径向基函数代替传统的全局响应的激发函数。经理论证明，径向基函数神经网络可以以任意精度局部逼近任意函数，而且训练过程极短。由于径向基函数神经网络在函数逼近方面有着明显的优势，故选取其作为对函数f（x）进行逼近的神经网络。

理想的RBF网络算法为

式中：x为网络的输入信号；ε为神经网络逼近误差；＊W为理想RBF网络的权值。

实际情况下，设RBF神经网络的输出为

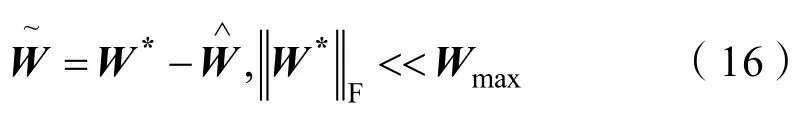
设计控制律为

式中v是鲁棒项，用于克服神经网络逼近误差ε。

将控制律式（17）代入式（6），得

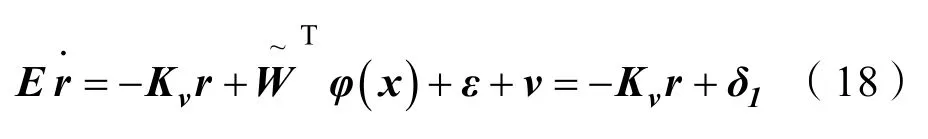
将鲁棒项设计为

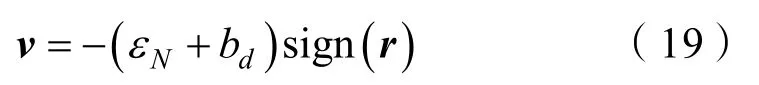
2.2.2 权值更新律的设计

设计的权值更新律必须满足使闭环系统跟踪误差稳定的要求，而且在跟踪输入误差r足够小的情况下，权值更新律必须为可证有界的。本文设想采用在线更新权值的方法，不需要额外离线更新权值的步骤，可以保证控制器具有更佳的实时性以及自适应性。另外，设定权值初始化为 0，因为控制器具有一个跟踪环可以保证跟踪误差是有界的，从而神经网络可以开始学习，即权值更新。

2.2.3 稳定性分析

利用Lyapunov定理分析稳定性，定义Lyapunov函数为

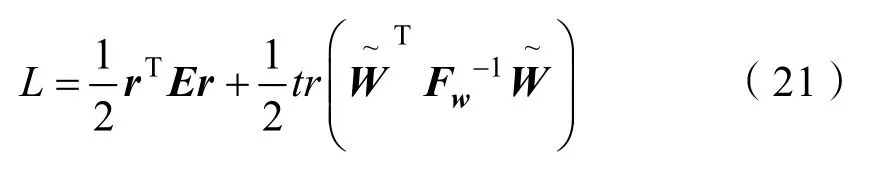
式中，E和Fw均为正定阵。对L求一阶导，有

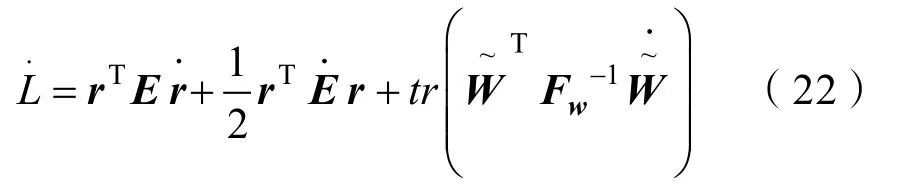
将式（18）代入式（22），得

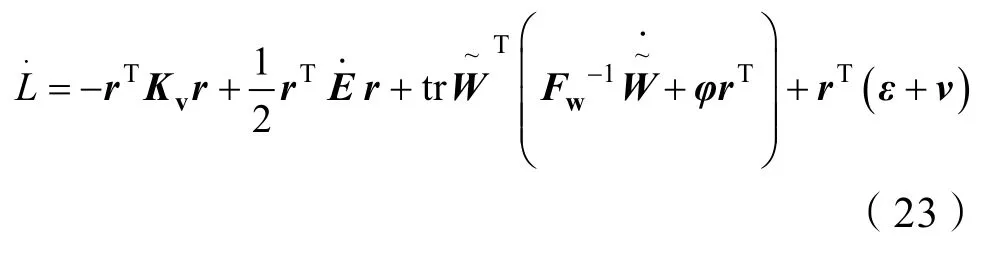
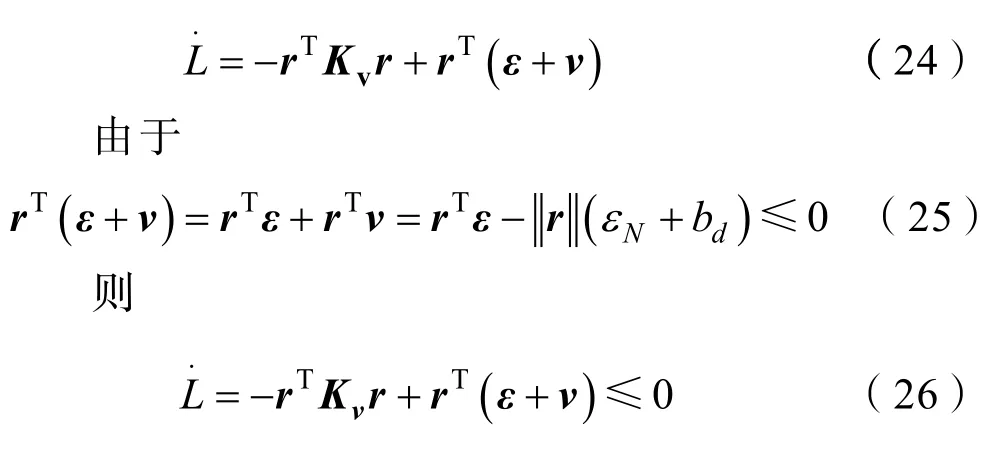
由于当且仅当r=0时，即当时，r≡0。根据LaSalle不变性原理，闭环系统为渐进稳定，即当t→∞时，r→0，系统的收敛速度取决于Kv。

又

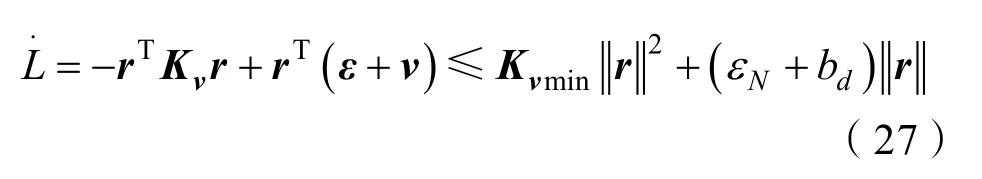
式中Kvmin是Kv的最小奇异值。因为εN+bd是常数，只要

综上所述，当神经网络的隐藏层有持续输出φ，且跟踪误差函数r是最终一致稳定并满足式（25），那么神经网络实际权值一定有界。

3 水下拖体姿态角控制仿真

假设某水下拖曳系统以恒定的速度直线运动，拖体为鱼雷型，式中部和尾部分别有定深翼板和控制翼板，拖体总长度为 2 400 mm，拖体直径为300 mm，重量为254 kg，拖缆直径为10.5 mm，单位缆长水中重量为0.07 kg/m。首先在3级海况下对水下拖曳系统的控制情况进行仿真分析，控制输入为均为有界，控制输出为将目标角qd（t） 设定为分别使用神经网络自适应控制器和传统PD控制器对拖缆和拖体进行控制，PD控制器的控制效果如图2和图3所示，神经网络自适应控制器的控制效果如图4和图5所示。

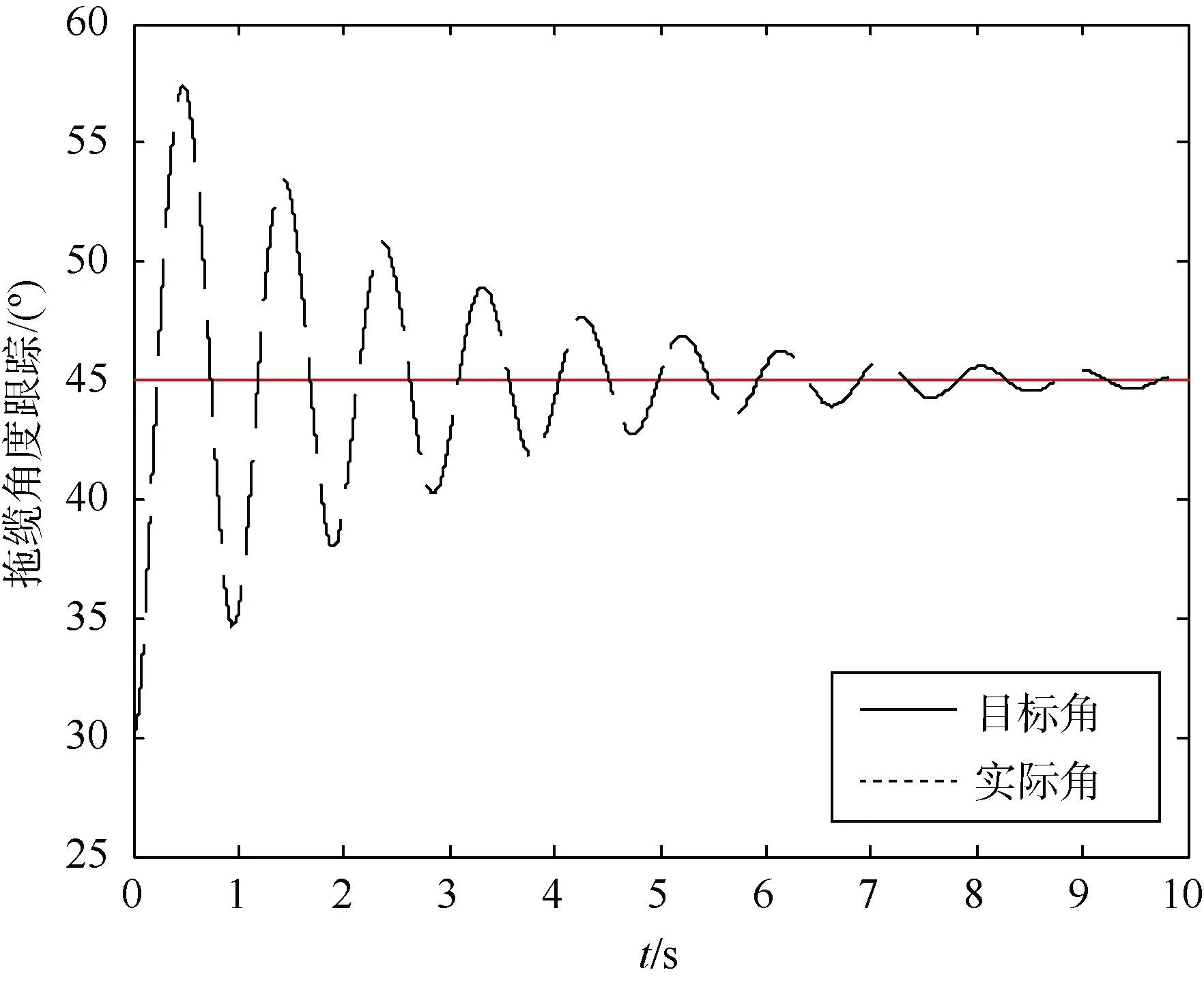
图2 3级海况下PD控制器拖缆目标角跟踪Fig.2 Cable target angle tracking of PD controller at 3-level sea state

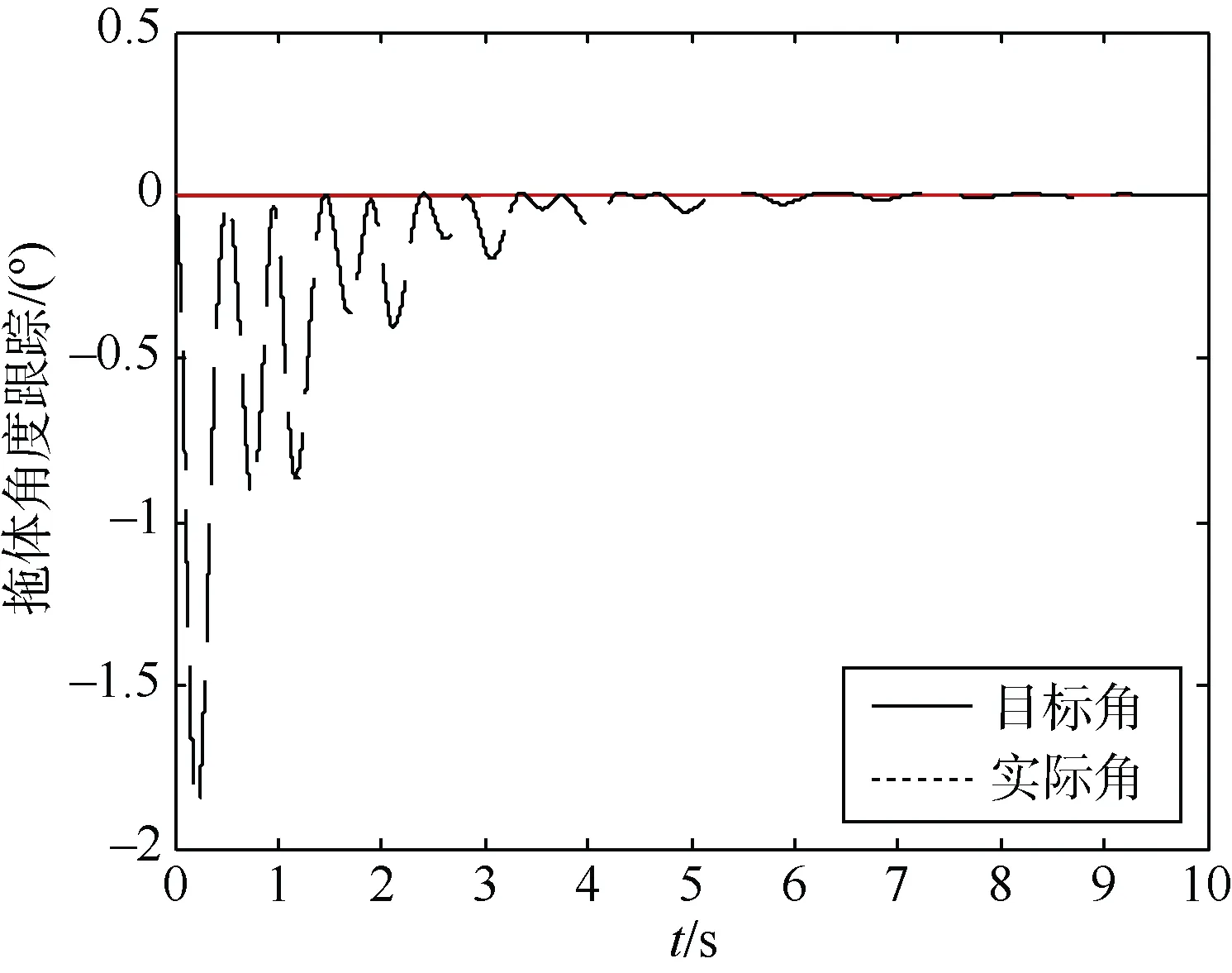
图3 3级海况下PD控制器拖体的目标角跟踪Fig.3 Towed vehicle target angle tracking of PD controller at 3-level sea state

图4 3级海况下自适应控制器拖缆目标角跟踪Fig.4 Cable target angle tracking of adaptive controller at 3-level sea state

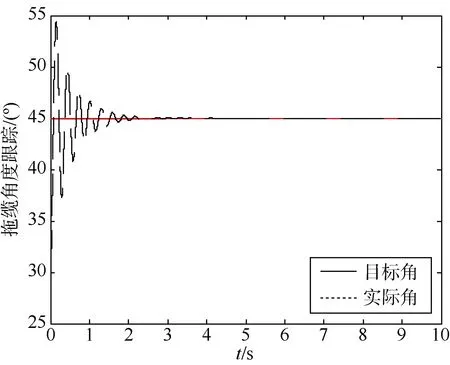
图5 3级海况下自适应控制器拖体的目标角跟踪Fig.5 Towed vehicle target angle tracking of adaptive controller at 3-level sea state

由上述仿真结果分析可知：PD控制器在4级海况下的控制效果劣于神经网络自适应控制器。对于拖缆，神经网络自适应控制器和 PD控制器的调节时间分别为2 s和8 s，稳态误差均趋于0。对于拖体，神经网络自适应控制器和 PD控制器的调节时间分别为2.5 s和5 s，稳态误差均趋于0。在实际情况下，水下拖曳系统可能会受到较为剧烈的海况影响，为了比较2种控制器在受到强烈干扰时的鲁棒性，将4级海况作为干扰输入，得到如下仿真图像：传统PD控制器的控制效果如图6和图7所示，神经网络自适应控制器的控制效果如图8和图9所示，神经网络逼近目标函数的情况如图10所示。

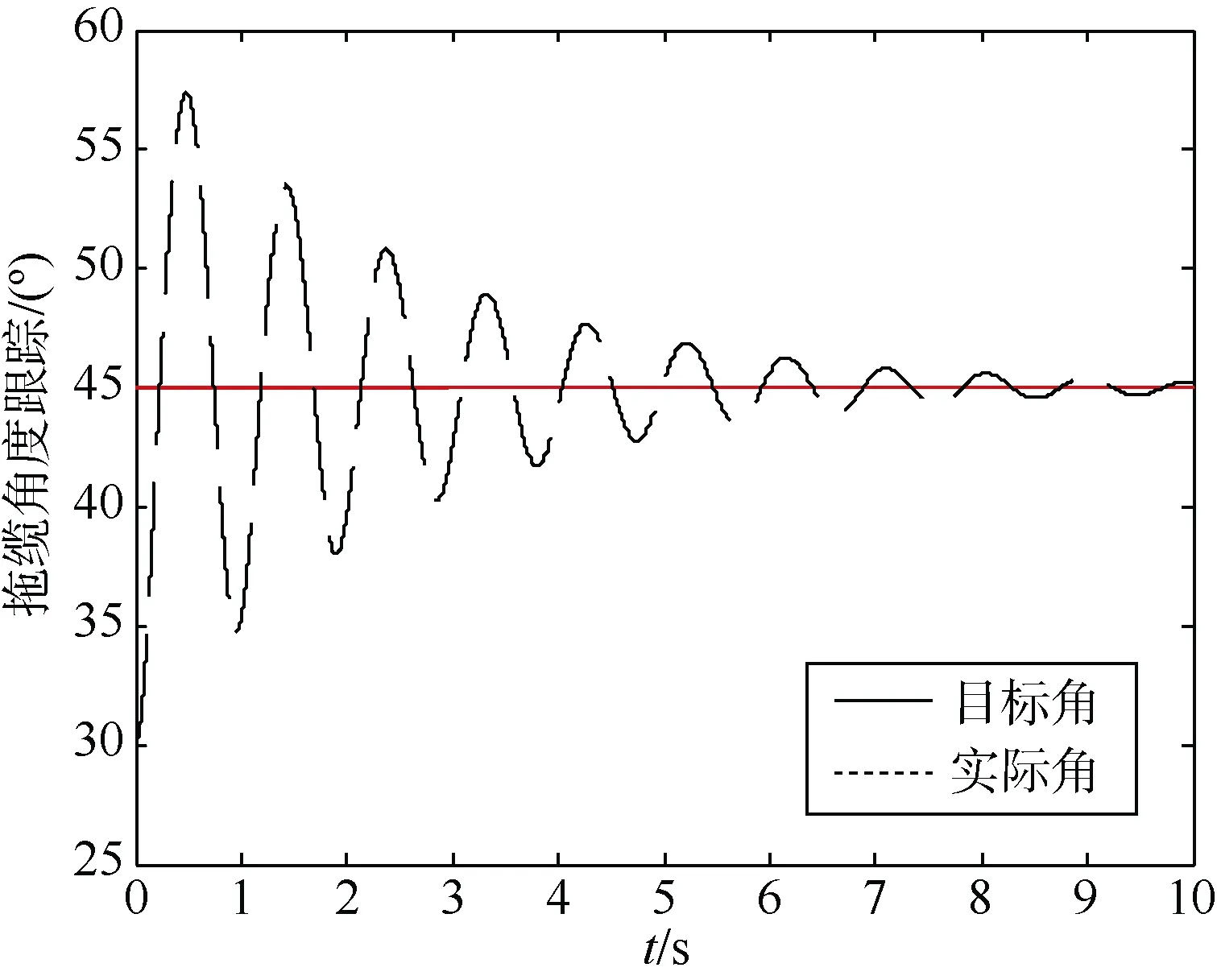
图6 4级海况下PD控制器拖缆目标角跟踪Fig.6 Cable target angle tracking of PD controller at 4-level sea state

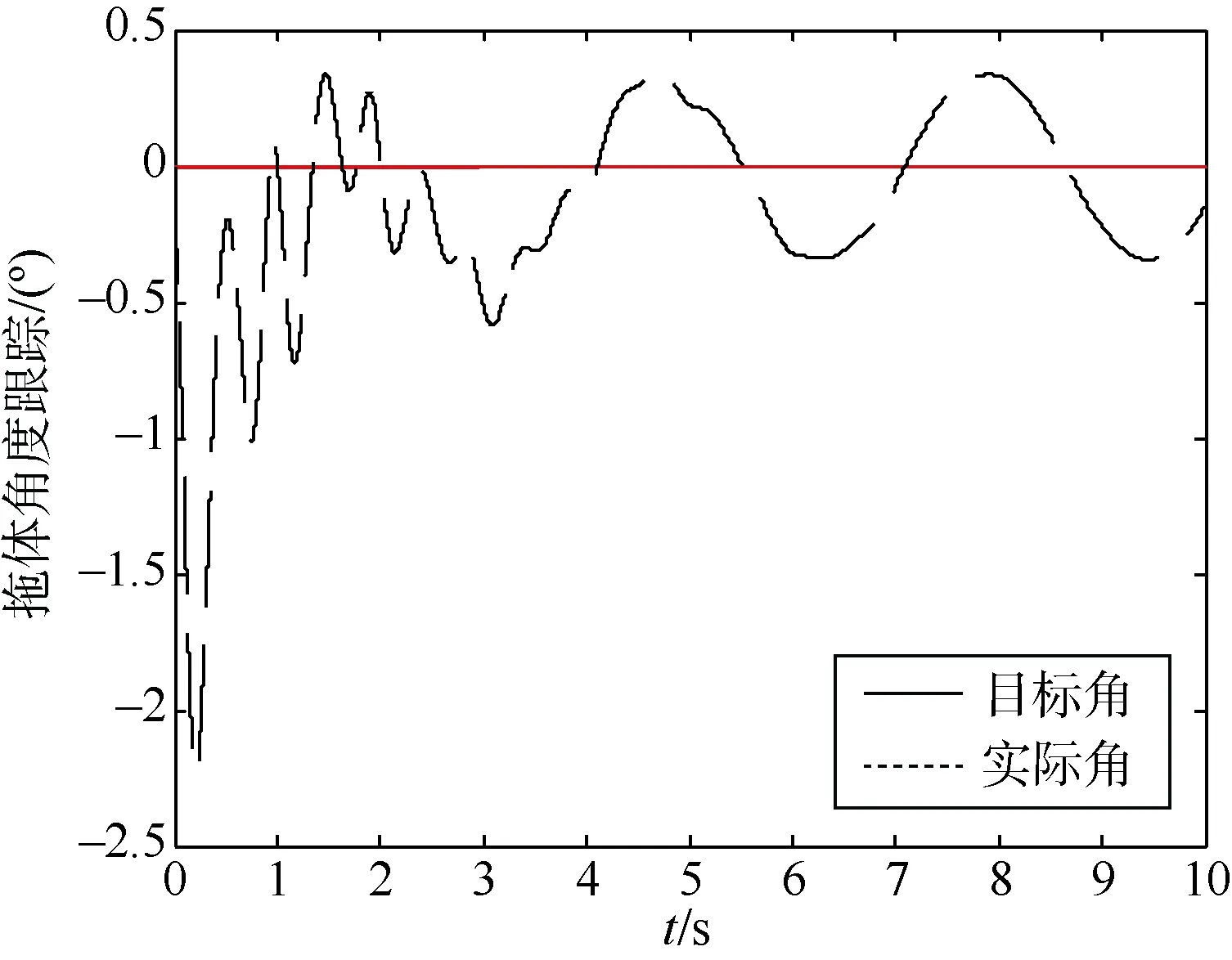
图7 4级海况下PD控制器拖体的目标角跟踪Fig.7 Towed vehicle target angle tracking of PD controller at 4-level sea state

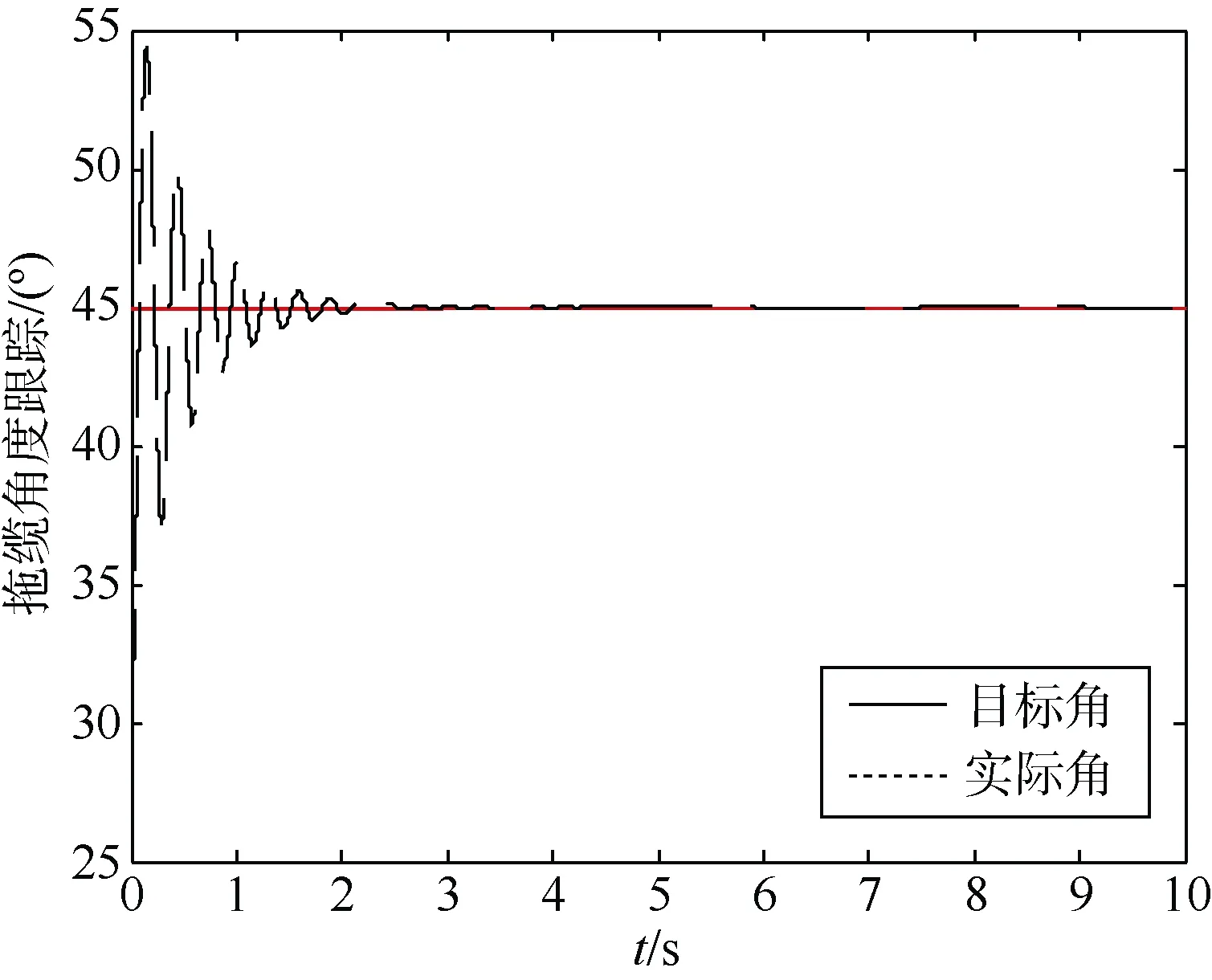
图8 4级海况下自适应控制器拖缆目标角跟踪Fig.8 Cable target angle tracking of adaptive controller at 4-level sea state

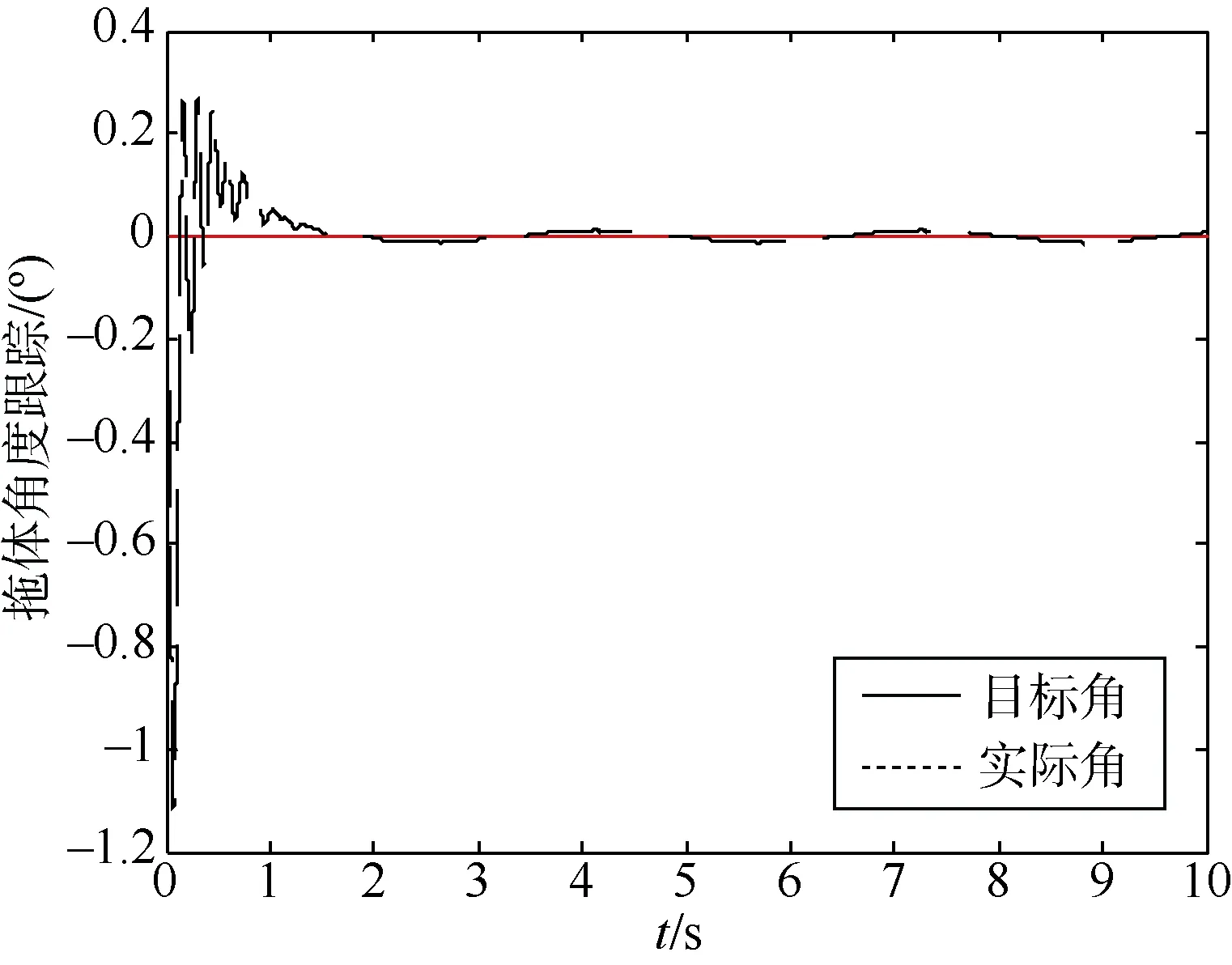
图9 4级海况下自适应控制器拖体的目标角跟踪Fig.9 Towed vehicle target angle tracking of adaptive controller at 4-level sea state

在5级海况下，由于PD控制器的参数无法实现自整定，所以当外界环境干扰产生较大变化时，PD控制器明显无法达到控制效果，实际角会在目标角的附近反复震荡，稳态误差较大，说明PD控制器无法起到抑制误差与扰动的作用，鲁棒性很差。神经网络自适应控制器通过在线学习，神经网络的输出可以较好地逼近模型中的非线性不确定函数项，很好地补偿了误差与扰动，在控制器参数选择合适的情况下，拖缆和拖体的角度完全可控，调节时间很短，稳态误差不大，可以达到控制目标。本文设计的神经网络自适应控制器可以看作是由RBF神经网络和PD控制器组成，工程上PD控制器是应用非常广泛的控制器，有着系统响应快，误差调整速度快的优点，但是遇到存在干扰的复杂环境时，PD控制器鲁棒性差的短板就显露出来，而RBF神经网络的存在很大程度上弥补了PD控制器鲁棒性差的劣势。

4 结束语

本文基于 RBF神经网络算法，并结合传统 PD控制器，提出了一种神经网络自适应控制器，该控制器在水下拖曳系统的垂直面二维运动控制中取得了良好的效果，该神经网络自适应控制器不需要繁琐的离线控制，也不需要其他线性控制器将非线性模型线性化的步骤，极大地保护了非线性模型自身的非线性特性。仿真实验表明，该控制器可以完成拖缆角度与拖体俯仰角的控制，并且在存在误差与干扰的情况下控制效果远优于PD控制器。如果将该控制器工程化，算法通过硬件加速后控制效果可能更好。本文的研究对于水下拖曳控制系统的设计来说有参考价值，目前仅仅是完成了垂直面上的二维运动仿真，对于更加复杂的三维运动控制问题，以及模型中n＞ 2的情况，将是下一阶段的主要研究方向。