基于李代数表征的三维物体空间姿态检测

(山东科技大学 机器人研究中心 山东 青岛 266590)

随着社会的不断发展，人口老龄化问题越来越严重，世界各国对人口老龄化问题越来越重视。针对老人和残疾人设计的助老助残机器人，在日常生活中为老人和残疾人提供基础的服务，提高他们的生活质量，能够在一定程度上缓解老龄化问题带来的社会压力。对于助老助残机器人而言，感知是十分重要的部分，通过传感器准确获取物体真实位姿，是实现自动化抓取实物等操作的关键。但目前机器人搭载的传感器一般采用激光雷达或者深度相机作为传感器，成本高且计算量大。面对真实环境中复杂的场景，如果能仅依靠RGB相机从二维图像中准确检测三维物体的位姿信息，将有效降低硬件成本和计算量。

传统的物体姿态估计方法大都基于人工的局部特征匹配等(例如SIFT[1])，但这些方法仅适用于纹理丰富的对象。对于纹理简单的对象，通常使用基于模板的匹配[2]或密集特征学习方法[3]，但该类方法通常对照明和遮挡很敏感，检测结果易受环境干扰。特征学习方法[4]比基于模板的方法具有更强的泛化能力，但也具有许多不足之处，例如前期需要耗时进行多阶段预处理来学习密集特征，要在产生粗略物体姿态位置之后，再进行姿态信息的精确优化等。

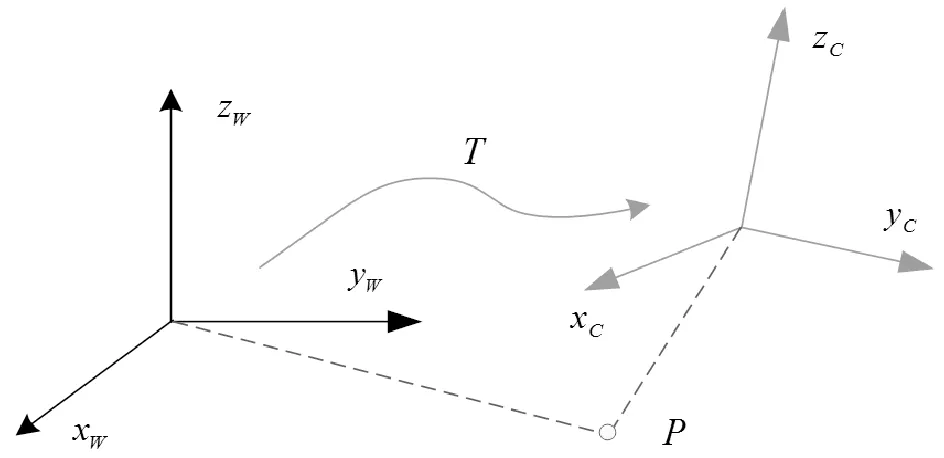
图1 三维空间物体坐标系列变换Fig.1 Three dimensional space objectscoordinate transformation

随着深度学习的发展，尤其是卷积神经网络(CNN)的兴起，二维图像中二维物体分类、检测以及语义分割等[5]方面都取得了显著的进步，但CNN对二维图像中三维物体姿态估计问题的应用却仍然有限。最近，有一些研究[6-8]应用深度学习从二维图像中进行三维物体姿态估计，但这些方法均不是端对端的训练方式。如其中文献[7]先估计粗略的物体姿态，再通过后期改进提高精度，大大增加运行时间。本研究将一种基于李代数的三维物体姿态表征方式与深度学习算法结合，运用李代数方程将旋转矩阵转化为向量，并利用卷积神经网络回归三维物体的旋转向量和平移向量，直接通过端到端的方式高效、准确地从二维图像中预测三维物体姿态信息，同时也大大降低了三维物体姿态检测的运行时间。

1 姿态描述方程

在三维空间中，一个刚体的运动可由旋转和平移组成。

旋转一般通过旋转矩阵、四元数和欧拉角来表征[9-10]。此时矩阵R由两组基之间的内积组成，刻画了旋转前后同一个向量的坐标变换关系，即矩阵R为旋转矩阵。旋转矩阵是行列式为1的正交矩阵，旋转矩阵的集合定义为：

SO(n)={R∈Rn×n|RRT=I,det(R)=1}，

(1)

其中，SO(n)是特殊正交群，这个集合由n维空间的旋转矩阵组成。SO(3)是三维空间的旋转，通过旋转矩阵可以准确描述相机的旋转。

平移也是欧式坐标变换中的一种。考虑世界坐标系中的向量a，经过一次旋转(用R描述)和一次平移t之后，得到a′，则：

a′=Ra+t。

(2)

其中，t为平移向量，相比于旋转，平移部分只需要把这个平移量加到旋转之后的坐标上，通过上式，可以用一个旋转矩阵R和一个平移向量t完整描述欧式空间的坐标变换关系[11]。

1.1 旋转矩阵和李代数

旋转矩阵描述了一个6自由度的三维刚体运动，其中矩阵R中有9个变量但每次旋转只能调整3个自由度，这种描述方式是冗余的；同时旋转矩阵必须是正交矩阵(即行列式为1)，这些约束会使得将旋转矩阵作为卷积神经网络的真实值进行梯度求导反向传播求最优解变得困难。

对于任意一个旋转都可以用一个旋转轴和一个旋转角来刻画，使用一个向量，其方向与旋转轴一致，长度等于旋转角，称为旋转向量，这种表示方法只需要一个三维向量即可描述旋转。旋转向量和旋转矩阵之间是可以转换的。设有一个旋转轴n、角度为θ的旋转，对应的旋转向量为θn，从旋转向量到旋转矩阵的转换过程由罗德里格斯公式完成，有：

R=cosθI+(1-cosθ)nnT+sinθn∧。

(3)

符号∧表示向量到反对称矩阵的转换符。

对于三维旋转矩阵构成的特殊正交群SO(3)，其对加法是不封闭的，而对乘法是封闭的(封闭即变换后仍是旋转矩阵)。对于任意旋转矩阵R，通过对矩阵的求导和在R(0)=I处进行一阶泰勒展开，可知其在SO(3)原点附近的正切空间上，同时在t0附近，设φ保持为常数即φ(t0)=φ0，将初始值R(0)=I代入，得：

(4)

so(3)表示SO(3)对应的李代数向量。至此，SO(3)和so(3)由指数映射给定：

(5)

由此可知，旋转矩阵和旋转向量可由指数映射和对数映射互相转换。其中，每个SO(3)中的元素，都可以找到一个so(3)元素与之对应；但很可能存在多个so(3)对应同一个SO(3)，因为旋转角存在周期性的问题，在此处将其固定在正负180°之间，则李群和李代数是一一对应的，也就是其三维物体旋转矩阵和旋转向量的对应关系。

1.2 回归姿态向量与三维物体姿态向量转化

在仅利用二维图像来预测其中三维物体的姿态信息时，需要将数据集中给定的旋转矩阵与旋转、平移向量互相转化，此时利用李代数表征旋转和平移向量，将原来的学习矩阵简化为学习向量，大大降低了卷积神经网络的训练难度。

给定预测的旋转矩阵，即来自姿态网络预测的四维向量的前三维，使用指数罗德里格斯映射来映射它到相应的旋转向量[12-14]。为了准确计算平移向量，依赖于预测的z分量(tz-四维预测向量中最后一个元素)和预测的边界框坐标来计算两个缺失分量tx和ty。假设边界盒中心(在输入二维图片中)是三维检测物体重心(对象坐标系的原点)的投影点。在此假设下，使用三维-二维投影公式，按如下方式计算tx和ty:

(6)

其中u0，v0是二维图像中的边界框中心，矩阵[fx，cx，fy，cy]是已知的内部相位校准矩阵。

2 利用卷积神经网络优化三维姿态预测

为了实现整个卷积神经网络系统的端到端训练，本研究提出了新的训练方式，将二维图像作为输入，输出检测物体的三维姿态。这需要一种有效的方式来表征三维物体姿态，同时也要设计合理的损失函数来衡量预测结果的准确性。采用四维向量表征姿态，其中前三维向量表示姿态的旋转矩阵对应的x和y轴向量，最后一个元素表示姿态的平移向量的z轴分量。给定预测的z分量和来自三维边框回归分支的预测边界框坐标，使用三维物体投影属性来恢复完整的平移和旋转向量。三维物体姿态识别的结构如图2所示。

2.1 三维姿态表征

将三维物体投影到二维图像中时，对于平移向量，具有相同z轴分量和不同x轴y轴分量的两个平移向量可以产生两个在二维图像中具有非常相似的外观和比例的对象(在图像中的不同位置处)，且在平行投影的极端情况下，很难有效区分。这导致网络难以通过仅使用外观信息作为输入来预测平移向量的x和y轴分量。

设计姿态回归网络的关键之处是通过学习欧几里得空间的映射关系，输出三维物体姿态的平移向量，此过程不需要预测完整的映射向量，而是训练网络模型仅对平移向量z轴分量进行回归预测。

但表征姿态的旋转向量比平移向量要复杂得多。欧拉角因参数的明确含义易于理解，但欧拉角是以2π弧度环绕，即对于相同的旋转角会对应多个数值，这导致对单个标量进行回归训练是困难的，同时，基于欧拉角的表示方法还受到了万向节锁定问题的困扰；另一种思路是使用3×3正交矩阵进行冗余表征，但在通过反向传播训练网络时会产生强制正交性约束的问题，这种约束容易导致优化算法陷入局部极小值；而常用的一种表征方式是使用单位长度的四维四元数，但四元数表征的缺点是运算复杂且在某些情况下解不稳定。

图2 三维物体姿态识别模型结构Fig. 2 Structure of 3D object pose recognition model

本研究使用李代数与李群(三维旋转矩阵的空间)相关联作为旋转表示方法。李代数so(3)被称为李群so(3)的恒等元素处的切空间。之所以选择李代数so(3)来表示旋转，是因为so(3)的任意元素允许由R3中的矢量参数化的斜对称矩阵表示，表示的元素是连续且平滑的，便于卷积神经网络训练时进行反向传播，这意味着网络只需要回归三个标量，无需任何约束即可表示三维物体的旋转矩阵。在训练过程中，通过罗德里格斯公式对数映射将旋转矩阵的三维信息映射到对应向量中。在学习预测旋转矩阵时，映射的值用作回归目标值。所以，训练姿态网络目的是回归四维向量，其中前三个元素表示旋转部分，最后一个元素表示姿态的平移部分的z轴分量。

2.2 损失函数定义

为了训练网络，定义一个新的损失函数来训练三维物体的姿态坐标：

Loss=Lpose。

(7)

姿态网络中每个特征输出4个向量，表示旋转的李代数和平移的z分量。姿态回归损失Lpose的定义如下:

(8)

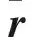
2.3 网络架构

采用网络模型Inception-Resnet,其中的Inception-resnet模块在Inception子网络的最后加入了一个1×1扩展卷积操作用于使其输出宽度(channels数目)与子网络的输入宽度相同，既降低了输出维度，也加入了非线性激励，提升了网络的表达能力。同时该模型在Inception的基础上增加了残差网络的思想，在网络搭建中加入了残差模块，能让网络设计更加深，具体模型架构如图3所示。

图3 Inception-Resnet网络结构(不同形状表示不同模块)Fig. 3 Structure of Inception-Resnet network (different shapes represent different modules)

在图3的模型结构图中，将网络划分为主干和分支网络两个部分。主干网络用于在整个图像上提取特征作为分支网络的输入。主干网络使用Inception-Resnet提取RGB图像特征，并输出4 096维的特征层，此特征层用作分支网络的输入。使用类不可知思想设计，即该分支输出单个预测结果，而不管类是什么。根据实验发现，这种设计降低了模型的复杂性和推理时间，有效提高了输出结果的准确性。

姿态预测分支网络由4个全连接网络组成，其中输出的数量为4 096→4 096→384→4。除了最后一层外，在每个完全层之后使用ReLU激活层，强化有效特征的输出结果。其中对于回归预测网络的全连接网络部分，本方法未做更多复杂的设计。

2.4 网络训练

使用Pytorch深度学习库实施整个模型架构[15]。卷积神经网络的输入是尺寸为299×299×3的RGB图像。因在训练调参过程中发现，相比于旋转向量，平移向量的学习误差更大，适当增大平移向量损失函数的比例可提高预测结果准确性，故姿态损失函数(13)中β值设定为1.5。姿态损失函数(13)的一个重要选择是回归范数p。通常，深度学习模型使用p=1或p=2，即利用L1范数或者L2范数来衡量预测值与真实值的误差，使用本文中用到的数据集，p= 1会得到更好的结果。端到端训练时使用随机梯度下降算法优化，其中动量参数为0.9，衰减系数为0.000 5。该网络模型在Titan X GPU上进行了50 000次迭代训练，每个训练批次输入4张图片(因其网络模型较复杂，占显存较大)。对于第一轮迭代过程，学习速率设置为0.001，然后对于剩余的迭代，学习速率减少为原来的十分之一。

2.5 结果测试

输入图像进行正向传播计算，选择RPN生成的前1 000个RoI(感兴趣区域)并将其输入分支网络进行框回归，然后进行非极大值抑制。基于分支网络的输出结果，选择具有高于特定阈值(0.9)的输出框作为预测结果，然后将姿态分支网络结果应用于检测三维物体姿态，其输出向量转化为三维物体姿态坐标。

3 实验结果与分析

3.1 实验结果

本研究在单个物体姿态数据集LINEMOD[6]上进行了模型预测结果评估，并与二维图像进行三维物体姿态估计的相关方法[6-8]进行结果比较。

度量标准：使用文献[7-8]中的标准指标。为了测量二维中的姿态误差，将三维对象模型投影到图像中预测估计姿态坐标并与真实坐标的区域进行交并比计算。如果两个检测框之间的交并比高于0.5(或者常用阈值如0.9)，则接受估计的坐标，该指标称为二维姿态评价指标。

对于测量三维物体中的姿态误差，使用5cm5°和ADD指标进行评价。在5cm5°度量中，如果在5cm的平移误差和5°的真实姿态角度误差范围内，则接受估计的姿态(越小越好)。在ADD度量中，如果由真实姿态构造的变换模型点云与估计姿态之间的平均距离小于检测物体直径的10%，则接受估计姿态(越小越好)。对于IoU的阈值一般使用0.5和0.9两个值作为评价标准来评价预测结果的准确度。

在文献[6]的数据集中包含杂乱场景中纹理复杂的物体，本研究仅使用RGB图像来评估。数据集包含12个对象序列，为了与文献[6-8]进行同等情况下比较，在可获得的12个三维物体序列上进行评估。每个对象序列中的图像包含多个物体，但是，只有一个物体使用真实值类标签和三维姿态，同时摄像机内在矩阵参数也随数据集一起提供。按照文献[7-8]中的评价标准，使用相同的数据集进行训练和测试：对于每个对象序列，随机选择30%的图像进行训练和验证，剩下的图像用作测试集，测试部分结果如图4所示。

3.2 结果分析

表1列出了本研究方法与Brachmann、BB8和SSD-6D在LINEMODE数据集[6]上进行二维和三维姿态检测的结果，共分为三个部分。其中第一部分是图像的二维误差矩阵比较，可见三种方法在二维检测的性能上并无较大差别；第二部分给出了本文与Brachmann[6]等对三维物体姿态估计精度的结果比较，其中方法Brachmann[6]、BB8[7]、SSD-6D[8]均使用二维图像作为输入来预测姿态。在5cm5°度量下，本文略低于BB8方法，而显著优于文献[6]，超过约39%。ADD指标方面，本方法的表现优于BB8方法，误差指标低于7.8%，且结果也比BB8更稳定。

图4 模型预测结果(深色框为预测坐标，浅色框为真实坐标)Fig. 4 Model prediction results (deep box is the predicted result; light box is the GT result)

从表1中对比可知，本文方法和BB8在5cm5°和ADD误差指标方面都比SSD-6D差。原因在于两个方面：一是SSD-6D不单使用来自数据集序列图像进行训练，更是在整个旋转空间上执行离散采样，并使用已知的三维对象模型生成图像用于训练。通过这种方式，SSD-6D的训练数据能够覆盖比Brachmann、BB8和本文方法更多的旋转空间，大大扩充了训练数据集的广度；二是SSD-6D还使用了基于ICP算法的改进方式来提高精度。而与SSD-6D相比，虽然本方法在评价指标上稍差，但本方法是端到端的训练方式，直接输出姿态而无需任何后处理，在保证一定准确率的前提下，提高了计算效率，达到了准确率和效率的平衡。图4展示了本方法在LINEMOD数据集上进行单个对象姿态估计的结果，可以看出，本方法能较好地预测三维物体的姿态。

表1 不同方法测试结果Tab.1 Test results of different methods

表2比较了本研究方法和其他方法的运行时间，其中Brachmann给出每张图像的运行时间约为0.45 s。本方法的端到端架构允许在Titan X GPU上每张图像的测试运行时间大约为0.08 s。SSD-6D和BB8相应的运行时间约分别为0.1 s和0.3 s。本方法和SSD-6D的测试速度相当，比BB8方法快4倍左右。其中，由于使用了后期优化方法，当输入图像包含多个对象时，SSD-6D和BB8的测试时间可能会随之线性增加。

表2 不同方法运行时间比较Tab.2 Results of operating time compared with different methods

4 结论

针对助老助残机器人识别和检测三维物体姿态坐标问题，提出一种基于李代数的三维物体姿态检测方法，用于从单张二维图像中预测三维物体的姿态信息。由于本研究方法采用端到端的训练方式，可以直接输出估计的三维物体姿态信息而无需任何后期优化。其中的创新之处在于使用李代数来表示旋转和平移向量，通过李群和李代数之间的转换来获取三维物体的姿态信息。本方法与目前主流的基于二维RGB图像的三维物体姿态估计方法相比在准确性和速度方面具有优势。但网络参数未针对速度进行优化，可通过精心选择参数来实现速度和准确度间的更好平衡，需在下一步工作中解决。