利用质量迁移指纹和GRACE数据解算地心运动

(1. 福州大学 空间数据挖掘与信息共享教育部重点实验室，福建 福州350108；2. 闽江学院 海洋学院，福建 福州 350108；3.代尔夫特理工大学 地球科学与遥感学院，荷兰 南荷兰省 代尔夫 2600AA)

地表质量，包括大气、海洋、冰川、陆地水等，不断交换、迁移，致使固体地球形心(center of figure， CF)与地球质心(center of mass， CM)时刻处于相对运动中。采用国际地球自转和参考框架服务机构(the international earth rotation and reference system service，IERS)的建议，将CM定义为地心，CM相对于CF的运动即为地心运动[1]。

地心运动分量ΔX,ΔY,ΔZ与地球重力场模型的一阶项系数ΔC10,ΔC11,ΔS11相对应，即[2]：

(1)

其中：a为地球平均半径；k1为一阶弹性负载勒夫数，其值取决于坐标系的选取，例如，在CF坐标系中，k1=0.021[2]。以下为了简洁，省去公式中的Δ符号，但均应理解为时变信号。

重力恢复与气候实验(gravity recovery and climate experiment，GRACE)重力卫星的成功，空前提高了地球时变重力场模型的解算精度和分辨率，首次实现人类对地球系统中大规模质量迁移的直接观测，加深了对气候变化影响的理解[3]。GRACE任务采用低-低卫星跟踪卫星方式获取观测数据，两颗卫星始终环绕CM运动，因而无法获取CM相对于CF的运动信息，即无法获得地心运动数据。因此，基于GRACE数据解算的地球重力场模型不包含一阶项系数。

为填补GRACE重力场模型的一阶项系数，可采用包含该信息的其他卫星数据，如卫星激光测距(satellite laser ranging，SLR)数据。但由于目前SLR地面观测站数量稀疏，且集中于北半球中纬度地区，所得结果误差较大。Blewitt等[4]利用全球分布的GPS地面站点探测地表形变，反演地表质量迁移，解算地心运动。该方法虽得到一定推广[5]，但由于其无法解算地心运动的趋势，在GRACE重力场模型用户中未得到广泛应用。目前GRACE数据处理中使用最为广泛的方法是由Swenson等[6]首先提出的基于GRACE数据和洋底压力(ocean bottom pressure，OBP)模型的GRACE-OBP方法。其基本思路是利用洋底压力模型获取海洋各点在CF坐标系中的质量变化，利用GRACE数据获取这些点在CM坐标系中的变化，认为二者差值是由于一阶项缺失所导致的，从而可以利用最小二乘法反算一阶项。随后，Sun等[7]对该方法进行了改进，使之可以同时解算C20；并利用模拟数据确定了该方法的最佳参数组合以便获得最优的地心运动周期项估计[1]；通过结合输入数据的误差信息得到统计最优的地心运动[8]。GRACE-OBP方法依赖于精度未知的OBP，最终得到的地心运动结果精度难以评定。

近年来，指纹法在全球及区域海平面变化研究中得到初步应用。Rietbroek等[9]通过建立指纹数据集，结合GRACE和卫星测高数据，解算了全球及区域海平面变化。Sun等[10]利用GRACE数据和指纹数据集解释了C20变化。与GRACE-OBP方法相比，指纹法不直接依赖地球物理模型，且可以给出地球系统各个分量的贡献。本研究旨在利用GRACE和指纹数据集解算地心运动。

1 算法介绍

由于自吸引效应(self-attraction and loading effect)，地表任一点的质量变化都会导致全球性的质量迁移，从而造成全球重力场变化。本研究将点P(θ，φ)处的单位质量变化所导致的全球性质量重新分布模式定义为指纹fM，可以在频率域内展开，以球谐系数形式表达。

假设某点或某区域发生单位质量变化，可利用海平面方程(参考Tamisiea等[11]公式(1)～(5))计算相应的fM。当该点或该区域质量变化为αfM而非单位质量时，所导致的全球质量变化可表示为αfMfM。将各点质量迁移所导致的全球质量变化叠加即可得到GM：

(2)

其中：FM为fM的集合；m为指纹个数；n为每个指纹展开至某一阶次所包含的球谐系数的个数；α为指纹的系数向量。由于质量系数可由重力场模型的斯托克斯(Stokes)系数通过简单转换来求解[13]，即：

(3)

其中：ρ为地球平均密度；l为阶数；kl为l阶弹性勒夫数。因此，公式(2)可转化为：

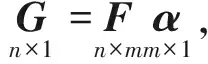
(4)

其中，F为f的集合，G由GRACE月重力场模型提供，因此一阶项缺失，f则为一套包含一阶项的球谐系数。另外，由于GRACE重力场模型的C20不准确，本研究假设其未知，与一阶项同时解算，因此公式(4)应写成：

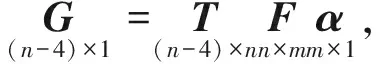
(5)

其中T为截断矩阵：

(6)

其作用是消掉f中的C10，C11，S11和C20，从而与G中的系数保持一致。为便于理解，假设只需要5个指纹：1个ANT(南极，Antarctica)指纹，1个GRE(格陵兰岛，Greenland)指纹，1个GLA(陆地冰川，glaciers)指纹，1个TWS(陆地水，terrestrial water storage)指纹和1个GIA(冰川均衡调整，glacial isostatic adjustment)指纹，则公式(5)可以进一步展开为：

(7)

当残差G-TFα较小时，可以认为对地球系统的区块或模式划分比较合理。注意，α通过最小二乘法求解，理论上G中只需包含4个系数即可(仅需解算4个未知数)，但使用较多的系数有利于减少系数误差对于结果的影响，使得求解稳定精确。同时应注意，某一时刻f中的所有系数均对应同一个αf，也即利用C21及以上系数所解算的αf也适用于一阶项和C20。因此：

(8)

利用GRACE重力场模型月解(不包含一阶项，去除C20)，可以得到该模型的一阶项和C20。利用该方法，每月解算一组，最终形成时间序列。不仅可以得到总的一阶项时序，还可以得到各个贡献源的分量，即：

(9)

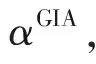
(10)

式中，mk表示第k个月份，前后两个月份分别表示为mk-1和mk+1。

图1展示了对GIA相关指纹所采用的时域约束。注意图1中贡献源仅为4个，共包含1个ANT，1个GRE、1个TWS和2个GIA共计5个指纹。在实际解算过程中，为了使所添加的约束有效，需要令其有较高的权重。由于指纹系数一般小于10-3量级，因此采用图1所示约束即可。

该示意图仅展示当GRACE月重力场模型为4个，贡献源数量为4个，指纹数据量为5个(包含2个GIA指纹)的情况。对GIA贡献的约束通过设计矩阵下方增加行来进行，所对应的数值根据公式(10)在mk-mk-1=mk+1-mk的假设下得到图1 对GIA贡献进行时间域约束Fig. 1 Scheme of implementing the time-domain constraint on GIA contributions

2 输入数据

本节运用由美国空间研究中心(Center for Space Research，CSR)解算的RL06 GRACE月重力场模型(GRACE-Level2数据GSM)，包括从2003年1月至2016年8月共计149个月重力场模型。统一去除该时段内的平均重力场模型得到时变月重力场模型。由于地心运动主要受大规模质量移动影响，高阶项系数表达的中小尺度质量迁移对其影响较小，可以忽略，因此采用解算至60阶次的模型。另外，由于解算α所使用的系数达3 000多个，系数中的各种误差可以得到很大缓解[10]，对月重力场模型无需采用任何去相关、滤波处理，从而可以避免由此所导致的信号畸变。

参考现有指纹数据集建立方案[12]，建立了一套新的共包含161个指纹数据的集合。其中，将南极地区按照Zwally等[14-15]划分的汇水区分成27个区块；格陵兰岛则首先按照汇水区划分为8个区块，再利用2 000 m高程线将每个区块一分为二，形成16个区块。假设区块内各点的质量变化均一，区块内总质量变化均为1 Gt，分别计算其指纹。陆地冰川一般为点状分布，位置信息由世界冰山清单/空基全球陆地冰雪观测(world glacier inventory/global land ice measurement from space，WGI/GLIMS)[16]数据集提供。将聚集在一起的冰山群划归为一个区块，每个冰山群的总质量变化统一为1 Gt，但各点质量变化不同，与各点的冰山数量成正比。极地地区和陆地冰川的区块划分方案见图2。由于TWS变化比较复杂，很难用区块划分的方式进行解构，因此利用Water GAP全球水文模型(water GAP global hydrology model，WGHM)[17-18]解析出TWS分量的前60个经验正交分解函数(experiment orthogonal function，EOF)，针对每个EOF解算一个指纹。由于水文模型不能预测人为因素导致的质量变化，因此另外增加了印度地区指纹以便捕捉到该地区的地下水减少信号。注意，WGHM中与陆地冰川重叠的格网点需要事先去除。GIA指纹则是基于ICE-6G冰史解算的Fennoscandia 2个、Laurentide 3个以及南极地区1个共计6个区域GIA模型。

(a)南极冰盖的划分方式(27个区块)；(b)格陵兰岛冰盖的划分方式(16个区块)；(c)为陆地冰川集群，同时也展示了南极(10-20)和格陵兰岛(24-28)周边的冰川集群图2 极地冰盖及陆地冰川区块划分

3 结果与分析

将指纹乘以相应的系数并累加(即TFα)应能恢复实测全球GRACE全球重力场变化。图3(a)～(d)，展示了由原始GRACE数据解算得到的大地水准面变化，选取2003年1月、2006年6月、2009年9月和2015年12月作为示例进行展示(其他月份结果类似)。图3(e)～3(h)为TFα得到的结果，可见指纹法反演结果与原始GRACE数据的结果特征一致，且无明显条带误差。子图3(i)～3(l)和3(m)～3(p)分别与子图3(a)～3(d)和3(e)～3(h)类似，但展示内容为质量迁移。因此，基于该数据集所反演的地球重力场变化及地球系统质量迁移能够捕捉到大尺度变化特征，可以用于反演地球重力场低阶项。

(a)～(d)中分别展示了2003年1月、2006年6月、2009年9月和2015年12月由原始GRACE月重力场解算的大地水准面变化(未加入一阶项和C20)；(e)～(h)中分别展示了上述4个月份基于指纹法反演的大地水准面变化(TFα)；(i)～(l)展示了上述月份由原始GRACE月重力场解算的地表质量迁移(未加入一阶项和C20)；(m)～(p)中分别展示了上述月份基于指纹法反演的质量迁移

由于解算GRACE月重力场模型之前，大气及海洋去噪1B级(atmosphere and ocean dealiasing level 1B，AOD1B)产品所模拟的高频大气和海洋动力信号已经扣除，因此GRACE月重力场模型中不包含相应信号，所得一阶项结果中也不包含大气和海洋动力信号的贡献，可以直接用于补全GRACE月重力场模型。AOD1B产品的月平均值存储于GRACE Level-2产品GAC中，因此只需加上GAC产品的一阶项数据，即可得到地心运动总信号。图4展示了由指纹法得到的地心运动时序及其误差，并将其与基于GRACE-OBP法的结果进行比较。由于二者对应的GAC产品相同，即大气与海洋动力信号的贡献相同，图中所展示结果均未加入GAC产品的一阶项。

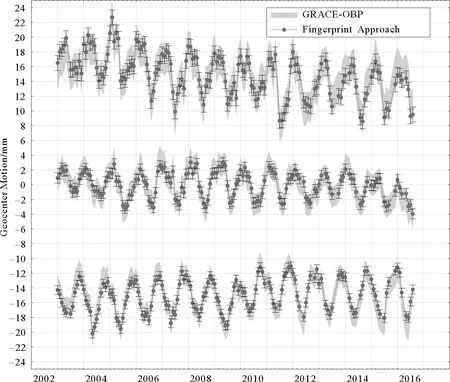
图中展示由指纹法解算的一阶项时序及其误差，并与由GRACE-OBP法解算的一阶项时序(条带的宽度表示其误差)进行对比。注意，所得结果未加入大气与海洋动力信号的贡献。为了易于辨识、在图中对所示时间序列进行了上下平移，由上至下以此为C10，C11，S11

表1给出了由指纹法解算的地心运动与其他方法结果的年周期振幅、相位及趋势信息。注意，为了与其他结果进行相比，表中基于指纹法和GRACE-OBP方法的结果均加上了大气和海洋动力信号的贡献。由表1可知，各种方法所解算的C10年周期振幅相差较大。Swenson方法解算的年周期振幅仅为1.9±0.1 mm，较其他方法小近1 mm。这是由于Swenson方法认为陆海质量交换时，流入、流出海洋的质量平均分布在整个海洋上。Sun等[1]利用模拟数据证明了该假设会严重低估地心运动C10(Z轴分量)的年周期振幅，考虑自引力效应对流入、流出海洋质量的分布影响之后，C10的年周期振幅明显增大，达到2.7±0.1 mm，也即GRACE-OBP方法给出的结果。基于指纹法的地心运动时序的年周期振幅达3.0±0.1 mm 与GRACE-OBP方法和Rietbroek方法接近。而基于GPS和SLR数据的方法所得到的年周期振幅普遍较大，相较基于GRACE数据的方法，差值超过0.5 mm。由于C10主要反映的是地心在轴方向的运动，因此与质量在南北半球之间的运动较为相关，南北极地区质量变化观测的精确程度成为关键因素，由于GPS和SLR在南北极地区的站点都相对稀疏，因此所得到的C10结果可能误差较大。变换解算方式发现所得C10的年周期振幅变化幅度可达0.6 mm，也反映了该方法所得结果的不确定性。C11和S11的年周期振幅(2.0±0.1 mm)介于Swenson方法和GRACE-OBP方法之间。Sun等[1]的模拟并未发现Swenson方法在C11和S11的解算中会造成较大偏差，因此仍具有可比性。表1中列出的各种方法所得到的C11年周期振幅一致，相差不超过0.2 mm。各种方法所得S11的年周期振幅也较为一致，只有Rietbroek方法的结果偏大，原因不明。

表1 地心运动时序周期及趋势统计

注：表中所统计的地心运动时序均包含大气和海洋动力信号的贡献

年周期相位方面，各种方法所得到的C11和S11结果相符，差别一般不超过2周。但是C10的年周期相位差别较大。基于GRACE数据的方法(包括GRACE-OBP[8，10]和指纹法)所得到的相位相较其他方法，如Wu等[20]使用的GPS反演法，差别较大(超过一个月)，其原因可能是GPS反演地面观测数据分布不均匀。

线性趋势方面，不同方法得到的结果差别较大。C10的趋势较C11和S11明显。指纹法所得到的趋势为-0.66±0.22 mmyr-1，与其他两种方法(Wu等[21]和Rietbroek等[19])的结果-0.88±0.09 mmyr-1和-1.08 mmyr-1符号一致但有一定差异。当单独考虑线性趋势的两个分量(PDMT和GIA)时，差别也较大。例如，指纹法得到的GIA分量只有其他方法所得结果的一半，这可能与目前GIA模型较大的不确定性有关。

与其他方法相比，指纹法的优势在于可以同时给出地心运动各个分量的贡献，有利于解释地心运动的驱动机制。图5展示了各信号源对地心运动的贡献。其中大气和海洋(atmosphere and ocean，AO)由AOD1B产品提供。可以看到，地心运动的三个分量的周期性变化几乎全部由TWS和AO引起。趋势项则主要存在于C10中，主要由格陵兰地区质量迁移信号所致。

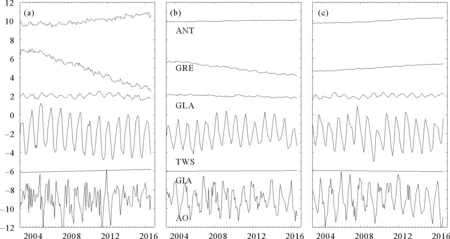
由指纹法解算的地球系统各个分量(由上到下依次为ANT，GRE，GLA，TWS，GIA和AO)对地心运动的贡献，其中AO分量由AOD1B产品提供。子图(a)～(c)分别展示了C10, C11和S11的结果图5 不同地心运动分量的贡献

4 讨论与结论

该研究表明指纹法可有效用于解算地心运动，也即地球重力场模型的一阶项时变。其中C11和S11分量的年周期振幅、相位均与GPS反演法和GRACE-OPB法所得结果吻合。C10的年周期振幅为3.0±0.1 mm与GRACE-OBP接近，但与GPS反演法的差别为0.3～0.9 mm。考虑到GPS反演法所得结果自身具有较大的不确定性(可达0.6 mm)，可以认为结果合理。Sun等[1]利用端到端的数值模拟证明了在参数选择合理的情况下GRACE-OBP方法可以准确解算地心运动；另外，Sun等[8]将各种方法所得一阶项结果用于补全GRACE重力场模型，并解算沙漠和南极东部地区质量迁移信号微弱的区域，发现使用基于GRACE数据的一阶项结果后可以有效消除研究区域质量迁移时序中的周期信号，这从两方面印证了GRACE-OBP和指纹法的结果较为合理。

与其他方法相比，该方法可以获取分布均匀且密集的数据，并同时给出地球系统各个分量对于地心运动的贡献，有利于理解地心运动的驱动机制。本研究结果表明，地心运动的季节性周期运动主要由AO和TWS两个分量驱动，且二者贡献相当；趋势项则主要由极地冰盖消融驱动。值得注意的是，格陵兰岛和南极冰盖的质量迁移对于地心运动的影响方向相反，但格陵兰岛作用明显强于南极作用。GIA也会驱动地心运动的长期趋势变化，本研究结果显示GIA对于地心运动的贡献很小，需要进一步研究确认。

本研究所使用的指纹法不仅是一种可行的地心运动计算方法，还具有其他应用潜力。例如，该方法所恢复的地球重力场没有明显条带误差的干扰，随着人们对质量迁移的认识不断加深，区块划分方案更加符合实际，利用指纹法恢复的月地球重力场模型将更加准确，其优势在于可以同时补充一阶项、改正C20和去除条带误差。另外，传统方法利用GRACE计算某一区块的质量变化时，由于其空间分辨率低，需要考虑信号泄露问题。而指纹法则可直接利用相应区块已知的质量分布结合通过最小二乘方法解算得到的每个指纹(区块)所对应的权重系数来计算其质量变化，避免了讨论信号泄露问题。