SA-BP神经网络在轨道电路故障诊断中的应用研究
徐绍俊
(西南交通大学 信息科学与技术学院,成都 611756)
25 Hz 相敏轨道电路的故障诊断比较复杂,具有不确定性。通常,设备维修采取的主要措施是使用万用表等仪器测量相关参数,结合人工经验和采集的参数数据进行故障诊断和分析。诊断结果取决于维修人员的经验和故障分析能力,因此,提供一个更为科学的轨道电路故障诊断方法具有现实意义。
文献[1]采用人工智能和专家系统的方法,提出了一种基于专家系统的故障诊断方法;文献[2]针对无缘轨道电路,提出利用遗传算法对其进行故障诊断;文献[3]提出采用基于自适应神经网络的模糊推理系统(ANFIS)的方法对音频轨道电路进行故障诊断;文献[4]提出采用D-S 分类器对轨道电路的电容缺失故障进行诊断;文献[5]提出将模糊神经网络(FNN)应用于轨道电路的故障诊断;文献[6]提出基于故障树分析(FTA)与改进BP 神经网络相结合的轨道电路智能故障诊断方法;文献[7]将粒子群算法(PSO)用于支持向量机的参数优化,提出基于粒子群支持向量机的故障诊断模型,并将其运用于轨道电路中。
本文根据25 Hz 相敏轨道电路的故障特点,在上述方法的基础上,改进轨道电路的诊断模型,提出一种基于SA-BP 神经网络的轨道电路故障诊断方法。BP 神经网络是通过负梯度方向更新网络的权值,但实际问题的求解空间是复杂的多维曲面,存在许多局部极小值;模拟退火(SA,Simulated Annealing)算法具有全局搜索能力,能够逐步收敛于整体最优解集,从而避免陷入局部极小值。
1 模拟退火与BP神经网络
1.1 模拟退火算法
SA 算法是模拟物理学中固态物质的退火过程,其步骤为:(1)基于给定的初始温度T0,通过状态产生函数产生状态S=S0;(2)对当前温度下的状态Si重复执行Metropolis 接受准则,满足内循环终止准则时退出;(3)开始降温程序;(4)重复执行(2)和(3),满足外循环终止准则时退出。
其中,状态产生函数是快速模拟退火算法的状态产生函数[7]:

式中,∆mi表示在当前状态下的扰动;ti表示当前温度值;mimax、mimin分别表示参数的上下限值;ui表示[-1, 1]区间上的随机数。
在模拟退火过程中,各状态接受条件的依据是Metropolis 接受准则,即:假设在温度T下状态为i时,其对应的能量表示为E(i) ;从状态i转变到状态j时,接受状态j为下一状态的概率为P(i→j),如式(3)所示,否则仍保留状态i为当前状态。
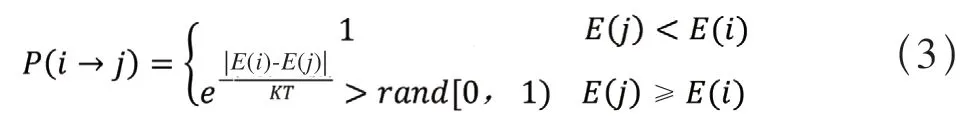
式中,K为玻尔兹曼常数,rand[0,1) 表示[0, 1)区间的随机数。
1.2 BP神经网络
BP 神经网络最早由Rumelhart、McCelland 等科学家提出,是一种简化人类大脑神经工作的生物模型。该网络由3 部分构成:输入层、隐藏层、输出层。组成结构如图1 所示。
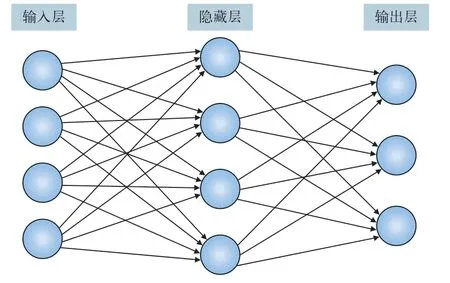
图1 BP神经网络简示图
BP 神经网络通过向后反馈学习的机制不断调节修正神经网中各个神经元的权值,最终输出正确结果。在神经网络中,输入层的神经元是接受来自外界的刺激;隐藏层和输出层的各神经元在学习机制中的数学关系如式(4)所示。

式(4)中,yi表示神经元接收到刺激;wij表示神经元的权值;xj表示神经元经过加权之后的值。
神经元经过接受刺激和权值加权之后,还需要对该神经元激活。对于神经元本身输出的激活函数,通常选取Sigmoid 函数,该函数如式(5)所示:

向后反馈学习调节修正各神经元权值的过程如下。
(1)计算网络输出值与期望值之间的误差

式(6)中,yj表示网络输出值;dj表示期望值;∆E表示网络输出值与期望值之间的误差。
(2)计算与神经元权重wij之间的误差量

根据式(4)可得:

而:

由式(6)、(7)、(8)、(9)、(10),可得:
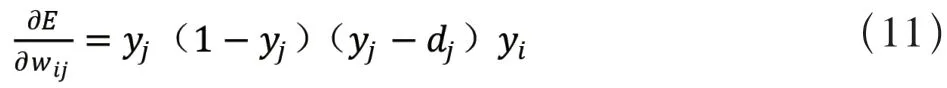
(3)设置学习率η

1.3 SA-BP神经网络
BP 神经网络在对神经元权值调节修正的过程中,容易陷入局部极小值。通过使用SA 算法,让网络具有较高的 “温度” 和 “能量”,使网络避免陷入局部极小值,而随着降低 “温度”,“能量” 也随之降低,又使网路避免跳过全局极小值[8]。在运用SA 算法过程中,主要难点在于如何判定BP 神经网络已经陷入了局部极小值。本文中的判断方法是在训练过程中判断误差改变量,若连续两次小于给定的常数值,则说明网络陷入了局部极小值,开始调用SA 算法。
SA-BP 神经网络算法的步骤为:
(1)对BP 神经网络的参数初始化;
(2)样本数据归一化处理;
(3)网络计算得到输出值E;
(4)若网络输出值E与期望结果Egoal 满足误差范围,则退出,否则跳转到步骤(5);
(5)反馈调节修正神经元权值;
国内外对知识融合的研究主要有3个方面:知识融合的模型或框架构建研究、知识融合算法或机制研究、知识融合在不同领域的应用研究。较之国外,我国的知识融合理论与实践研究水平仍有待提高。而目前构建的知识融合框架大多以一个特定的应用领域作为研究背景,还未形成一个权威的、能够为多领域所通用的体系结构。
(6)判断是否陷入局部极小值,若没有则跳转步骤(3),否则调用SA 算法;
(7)初始化SA 算法中的参数;
(8)扰动产生新的权值;
(9)调用Metropolis 接受准则,若新状态接受,跳转步骤(10),否则跳转步骤(8);
(10)判断是否满足内循环终止条件,若满足,跳转到步骤(3),否则跳转步骤(11);
样本数据归一化处理的公式如下:

式中,Xmax表示样本数据X中的最大值;Xmin表示样本数据X中的最小值;分式上下加1 是避免产生分母为0 的情况。
2 基于SA-BP神经网络的25 Hz相敏轨道电路 故障诊断
2.1 模型参数的选取
本文采用SA-BP 神经网络对25 Hz 相敏轨道电路建立故障诊断系统,针对25 Hz 相敏轨道电路的工作原理,选择送电端供电变压器输出电压、轨道电路接收端轨面电压和二元二位继电器轨道线圈电压作为网络的输入参数;选取4 种常见的故障作为输出参数[5],如表1 所示;利用文献[5]中收集到的25 Hz 相敏轨道电路数据进行分析与验证,部分数据如表2 所示。
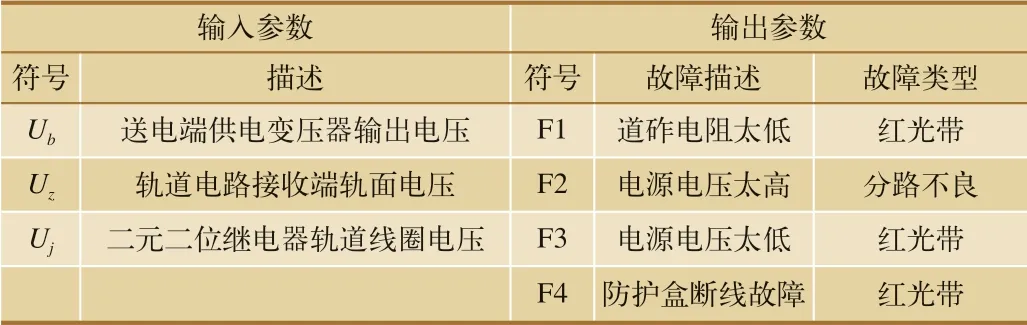
表1 模型输入和输出参数
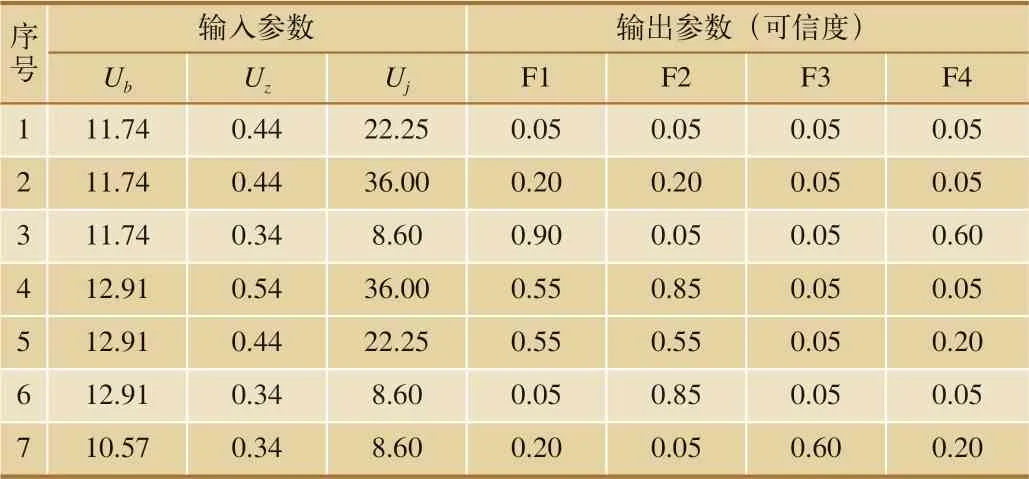
表2 SA-BP神经网络的学习样本
输入层的神经元数目n对应输入参数,所以n=3 ;输出层的神经元数目m对应输出参数,所以m=4 ;隐藏层的神经元数目根据经验公式h=2n+l[9],得h=7,即网络结构为3-7-4 型,最大误差设置为0.000 01 ;最大迭代次数设置为10 000 次,学习率η设置为0.7。SA 算法中的降温函数选取指数降温函数Tk+1=λ(k)T0,λ为降温系数,设置为0.95 ;初始温度T0设置为100 ;内循环终止准则即执行Metropolis接受准则时的阈值设置为500。
2.2 结果分析
根据前文的SA-BP 神经网络和表2 的学习样本,在神经元激活函数、初始权值和学习率都相同的情况下,分别使用传统BP 神经网络和本文提出的对SA-BP 神经网络在Matlab 2013a 中进行训练,训练时间和相对误差如表3 所示。

表3 两种方法下的训练时间和相对误差
分析表3 可知,SA-BP 神经网络比传统BP 神经网络的训练时间更短和相对误差更小。
3 结束语
本文针对25 Hz 相敏轨道电路故障诊断,提出SA 算法与BP 神经网络相结合的方法,运用SA 算法的优点,避免BP 神经网络陷入局部极小值,缩短训练时间和提高故障诊断的准确率。通过Matlab 仿真,验证了运用SA-BP 神经网络对25 Hz 相敏轨道电路进行故障诊断的有效性,可有效提高故障诊断的效率和准确度。

