变中寻不变玩中悟本质——《“半个”长方形》教学

蔡小钢 赵国防（特级教师）

多年的教学实践中常常遇到这样一种问题：在组合图形面积的计算过程中，学生思维不够活跃，思路不够开阔，稍复杂一点的题目便会“卡壳儿”。这到底是为什么呢？经过个别访谈和专项调研，我们发现，从基本图形的面积计算到组合图形的面积计算，之间有一道思维之“坎儿”，而教材中恰恰缺少跨越这道“坎儿”的内容，于是便开发了本课，一经实践，效果明显。

【教学过程】

一、创设情境，激趣导入

（由生活中的人物照片引出课题）

师：今天我们学习在长方形中寻找“半个”长方形。

说明：如果把长方形分成两个部分，一部分是“半个”长方形，另一部分也是“半个”长方形。

二、多种方式，找寻“一半”

1.预热：动手折出“一半”。

师：这两个“半个”长方形有什么关系？

生：形状相同。

生：也有可能形状不相同，但是面积相等。

师：形状相同，面积肯定相等；形状不相同，面积也可能相等，这两种情况都可以看成“半个”长方形。我们先来研究两个部分形状完全相同的情况。

师：怎么把一个长方形分成形状完全相同的两部分？

（让学生用A4纸折一折）

课件出示：

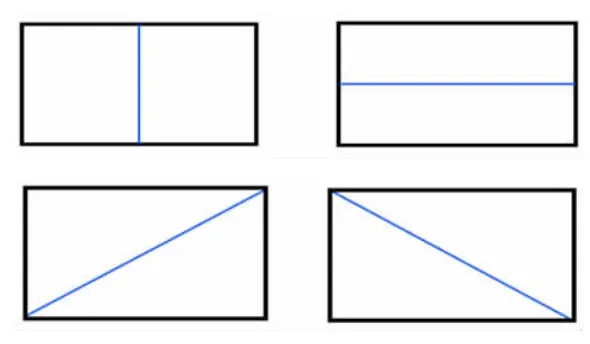
师：通过折一折，可以把长方形分成完全相同的两部分，它们都可以看成“半个”长方形。

2．发展：过中心画出“一半”。

师：如果把四种分法在一个长方形中表示出来，你有什么发现？

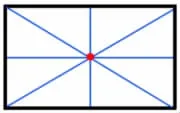
生：这个长方形被分成了8块完全相同的部分。

生：4条分割线都经过长方形中间的一点。

师：这个点我们通常叫做长方形的中心。猜猜看，还有什么分法也可能把长方形分成完全相同的两部分？

生：经过中心的一条直线。

师：怎么快速地找到长方形的中心呢？

生：画两条对角线，交叉点就是中心。

师：对啊！不用折，画一画就可以了！那这样的分割线真能把长方形分成完全相同的两部分吗？怎么证明？

生：量一量每条边，看这两部分的每条对应边是否相等。

生：沿着分割线剪一剪，比一比这两部分能否重合。

师：好办法！是否过中心的一条直线都能把长方形分成完全相同的两部分呢？

（引导全班学生画一画、量一量、剪一剪、比一比）

（学生操作，汇报）

结论：过中心的任何一条直线都能把长方形分成完全相同的两部分。

3.超越：两个图形找“一半”。

师：回顾一下，我们刚才通过四种特殊的分法，发现了4条分割线都经过长方形的中心，于是我们猜想一般的分法，通过动手操作验证了猜想，归纳出只要经过中心的任何一条直线都可以把长方形分成完全相同的两部分。

师：用刚才的发现来解决问题吧！想不想挑战？

生：（跃跃欲试）想！

师：你能用一条直线把下面两个长方形都分成完全相同的两部分吗？

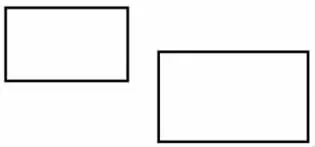
生：找到这两个长方形的中心，再把它们连起来！

生：（补充）还要把这条线段两端都延长！

师：你们太厉害了！根据两点确定一条直线，这条直线既经过小长方形的中心，又经过大长方形的中心，所以能把两个长方形都分成完全相同的两部分。

三、不断超越，在应用中创新

1.组合图形找“一半”。

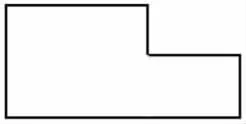
师：这个组合图形如何找到它的一半呢？

生：把它分成两个长方形，经过两个长方形的中心画一条直线。

师：哪里是它的一半？

生：把一个长方形的一半加另一个长方形的一半就是整个组合图形的一半。

师：有道理！（指一指，语调上扬）一半加一半就是整个图形的一半！

生：我有其他想法了！也是先把它分成两个长方形，只要分别经过这两个长方形的中心，再把各自的一半合起来就是组合图形的一半。

师：这个想法好！打破了我们固定的思维，用两条分割线分别找一半再把各自的一半合起来。

2.不过中心找“一半”。

师：根据刚才的思路，我们再回过头来看开始的长方形。（强调）不经过长方形的中心，是不是也能找到“半个”长方形？

生：我们把长方形先分成两个小长方形，然后分别找小长方形的一半，再把它们合起来。

生：（激动的）分成3个小长方形也行，找这3个小长方形的一半，再把它们合起来。

师：分成4个行吗？5个呢？

生：行！只要分别找一半，再把它们合起来！

师：（激动指出）这些分割线都没有经过大长方形的中心，但是……

生：分别经过了各自小长方形的中心。

3.判断联系，发散思维。

判断：下面哪些阴影部分是所在长方形面积的一半？

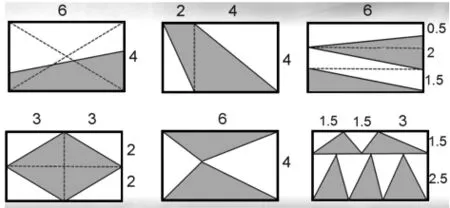
（学生汇报）

小结：我们已经知道过中心能把长方形分成完全相同的两部分，这两部分都是长方形面积的一半。通过刚才的学习，我们又发现不过中心也能找到。归根结底，只要把长方形分成若干个小长方形，分别找小长方形的一半，再把它们合起来就可以。

【点评】

作为一节自主开发的既基于教材又超越教材的生动课例，本课体现了以下三个特点。

一是立足学生研究，直面学生之“困”。学生在学了基本图形的面积计算之后，均能熟练地计算它们的面积，但在进行组合图形的面积计算时，却时常束手无策。这仅仅是因为组合图形涉及的图形数量多了，计算步骤繁了，运算量大了吗？不是的。经过大量实践与研究，我们发现，最主要的问题在于学生的思维没有打开，认知不够灵活，未能发现组合图形的本质，未能在变化中通过转化寻得其中的“不变”。蔡老师知难而上，根据学生学习过程中的实际困难，深入研究，精心设计，难能可贵。

二是重视思维训练，直指学习之“本”。深度学习，最大的特点便是思维的深刻性，而思维的深刻性不仅体现在对某一知识点的深刻理解，更体现在对所学知识的系统建构，活学活用。蔡老师借助半个长方形的变化，打开了学生思维——多种方式找到其中的“一半”，既将之前所学的知识点充分盘活，又让他们有了新的认识——要均分，就要过“中心”。尤其是找两个长方形的“一半”时，更充满了挑战。它既是对一个长方形找“一半”的巩固，也是一种变式和超越，将儿童思维引向了纵深。

三是重视思想渗透，直通学习之“魂”。数学思想是数学之魂，数学教学的过程，不仅是知识的探索与发现过程，也是数学思想的渗透与强化过程。在蔡老师的课上，在引导学生找寻长方形的“一半”的过程中，灵活多变，分类推进，民主开放，整体思想、分类讨论思想、隐含条件思想、类比思想、归纳推理思想、极限思想等都得到了巧妙渗透。