《填写数阵(1)》教学设计与思考
王张妮 王旭程
【教学背景】
本节课内容选自张天孝老师主编的《“学数学长智慧”超市》“构建等式1”第18至21页。《“学数学 长智慧”超市》是一套关注儿童思维发展和数学潜能开发的教辅材料,“构建等式1”中,特别设计以数阵作为“和相等”结构(□+□=□+□)的重要应用情境,训练儿童的概括能力和推理能力。我们针对其中“简单数阵填写”的部分,在一年级(下)开展了系列实验,期望通过实证研究,观察该阶段儿童是如何观察数阵并解决数阵问题的;通过教学,儿童对数阵问题可以达到怎样的解题水平。
【内容与设计】
本节课是在学生具备建构“和相等”的等式(从1~9的数中选择不重复的四个数填入方框,使“□+□=□+□”成立)的经验基础之上,设计的一节“填写数阵”探究课。前期,学生已经掌握了基本的“大数配小数”的方法,以及有序构建等式的策略;同时在进行等式的观察过程中,对“和相等”的基本性质(即一个加数增加几,另一个加数减少几,和不变)有一定的感性认知。在此基础上,这节课依次以“简单数阵——三角形数阵——十字数阵”为内容载体,试图通过教学来观察学生是否能在变化的数阵中找到不变的“和相等”结构,并通过“辅助探究——半开放探究——开放探究”三个层次螺旋推进教学,促进学生在逐渐“变化”的问题中寻找不变的结构。
【教学过程】
一、从简单数阵起步,明晰基本结构
1.阅读题意,自主探究。
出示题目:选 1、2、3、4、5、6、7、8、9 填入○中,同一个数不能重复,使每一边的和是15。

师:这是一个“人”形数阵,仔细阅读题目,如果你是小老师,你会提醒其他同学注意哪些问题?
在学生回答的基础上提炼、强调:选数范围是1~9;选数规则是每个图形中的五个数不能重复;运算规则是左边三个数的和等于右边三个数的和。
2.分层汇报,推进思考。
(学生自主探索后,指名汇报中间数是5的数阵)
生:左边填1和9,1+9+5=15,右边填3和7,5+3+7=15。
集体判断,对照前述三个要点(即选数范围、选数规则、运算规则)肯定其答案的正确性。
(出示动画:分别框出左边三个数和右边三个数)

生:我有一个新的想法,让左下两个数的和凑10,右下两个数的和也凑10。
师:可以吗?怎么从题目里说的三个数相加等于15变成了两个数相加等于10?这样做对吗?
生:我觉得可以。左边10+5=15,右边也是10+5=15。(指5)就是中间这个“5”重复用了两次。
师:大家听得明白吗?
生:我听明白了。就是每条线上已经有一个数5了,剩下的两个数凑10就可以。
生:“5”是重复数。
(教师配合学生介绍的方法,出示幻灯片,动态显示5用了两次,并进而动画形成○+○=○+○,从数阵中抽象出和相等的等式)

师:你们喜欢哪个方法?为什么?
生:当然是第二种方法,题目变简单了。
师:我也喜欢第二种方法。在第二种方法中,我们找到了一个重复计算的数——5,把题目变得简单了:从三个数为一组朋友,相加得15,变成了两个数为一组朋友,相加得10。
(出示幻灯片,逐一出示“重复数”“朋友数”)

小结:在解决问题的时候,如果我们能仔细观察,好好分析,常常能够找到比较简单的解决办法。
【设计意图:前测数据表明,学生的解题策略可以分为两个层次,第一个层次是停留在题目本意的理解上,即“左边三个数的和等于15,右边三个数的和也等于15”;第二个层次是在思考两边和同为15的过程中,意识到中间数5是一个特殊数,从而得到“左边两个数的和是10,右边两个数的和也是10”。看似一次简单地概括,其实已经触及问题的本质。因此,本环节有意识地收集了两个层次学生的作品,并分级呈现,在不同方法的碰撞中,引导学生思考、评价,进而提出“重复数”“朋友数”这样儿童化的概念,帮助学生积累分析数阵的经验。】
3.分类讨论,有序思考。
师:好,现在我们已经知道两边的朋友数要凑10,请你再填一填,你能得到几组不同的答案呢?
(学生尝试——反馈)
师:有的同学填了4组,有的同学填了6组。那我们请填得多的同学说说他是怎么填的?他填得对不对,好不好?
生:如果左边填1+9,右边填2+8;左边填1+9,右边填3+7;……
师:你们觉得这个方法好不好,理由是什么?
生:他的方法好,因为我发现他的填写有顺序。左边1+9,右边配上2+8、3+7、4+6;然后左边换成2+8,右边再依次搭配3+7、4+6;左边3+7,右边4+6。
(出示幻灯片,搭配图示)

师:如果把中间的5换成2或8,这时下面两个朋友数应该是几?你会填吗?
(学生自主填写并校对)
【设计意图:分类讨论、有序思考是重要的数学思想。在低龄学段,这样的思考方式还没有被完全建立起来,更需要创设情境,让学生多加感知。本环节从答案的多少这个问题深入,引发学生思考,如何“不重复,也不遗漏”的搭配策略,充分体验有序的思考。】
二、探究异形数阵,概括形式特征
师:想不到小小的数阵还有这么多讲究。怎么样?想不想再来挑战一个?
出示题目:把4、5、6、7、8五个数,填在每个图的○里,使每个三角形上三个数的和相等。
出示学生作品

师:他的答案正确吗?你是怎么检查的?
生:正确。左边三角形三个数的和是4+6+8=18,右边三角形三个数的和是5+6+7=18,两个三角形上三个数的和相等。
生:我有更快的方法。你们看4+8=12,5+7=12,所以答案肯定是对的。
师:(故作疑惑)为什么这样就对了?
生:和刚才一样。中间的重复数是6,左边三角形12加6等于18,右边三角形也是12加6等于18,两边的两个数加起来的和一样,答案就是对的。
师:谁听懂了他的意思?
生:中间的数,用了两次,其实是重复数,它旁边的两对数就是朋友数。只要两边的朋友数相等,两个三角形里数的和就也相等了。
师:你的意思是说,刚才的“人”形数阵中,我们找到了重复数和朋友数,把题目变简单了。这道“三角形”数阵的题目也能这样变简单,是吗?
(在学生回答的基础上,逐步出现动画,形成和相等的等式:○+○=○+○)

师:刚才是6填在中间,还有不一样的答案吗?
(学生汇报4、8填在中间的情况,全班一起验证答案)
师:5可不可以填在中间,为什么?
生:不可以,如果5填在中间,就找不到两组相等的朋友数了。
师:原来不是什么数都可以当重复数的,选择重复数的前提是剩下的两组朋友数要相等。对4、5、6、7、8来说,为了要让两边的朋友数相等,应该选谁来做重复数?
师:再看看,这些数在数列里排在什么位置?你有什么发现?
(学生检查,得到4、6、8分别位于头部、中间和尾部)
生:老师,我知道我知道,这个就像前两天我们填和相等的式子一样,去头、去尾、去中间,然后大数配小数就行了。
生:其实这个数阵就是填一个和相等的式子。
【设计意图:本环节有两个经验的调取:1.通过第一个环节“人”形数阵的探索,帮助学生抽象出“和相等”的结构,通过经验的类比,得到“三角形”数阵中“和相等”的结构,从而感知,数阵的外形变了,内在结构却没有变,仍然可以找到藏在数阵中的重复数和朋友数。2.通过对上一次实验中“和相等”等式建构策略经验的唤起,引导学生有序地填写数阵。】
三、拓展提升
师:大家的练习纸上有三个不同的数阵,用你们的火眼金睛,找出每个数阵中的重复数和朋友数,并小组交流。每位同学选一个最喜欢的数阵,填写答案,比比谁填得又对又好。
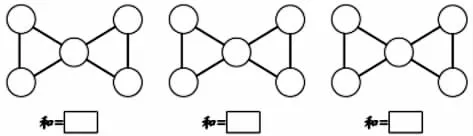
出示题目:把 4、5、6、7、8 五个数,填在每个图的○里,使每个三角形(变1、变2)或每条线上(变3)三个数的和相等。

师:哪个数阵最特别?为什么?
生:第三个数阵最特别,它的两个朋友数中间隔了一个重复数。
师:有时候,朋友数不一定靠在一起,需要我们仔细观察、思考。

题组答案数0组答案 1组答案 2组答案 3组答案百分比 变化率 百分比 变化率 百分比 变化率 百分比 变化率前测61.8%——22.4%——5.3%——10.5%——后测变1 10.70%-51.1% 16.0% -6.4% 13.3% +8.0% 60.0% +49.5%变216.0%-45.0% 13.3% -9.1% 16.0% +10.7% 54.7% +44.2%变333.3%-28.5% 12.0% -10.4% 10.7% +5.4% 44.0% +33.5%
有两组数据变化最为突出:第一组,0组答案的占比由前测的61.8%,锐减至变1、变2的百分之十几,可见原来得不出答案的学生,进行探究活动后,能够在自主练习中得到至少一组答案,我们认为这部分学生至少处于第二个层次。他们可以在教师的引导中,找到图形中的隐藏关系。第二组鲜明的变化数据是,得到3组(全解)的占比,由原先的10.5%增至近60%,在这些变化的题中,能够快速得到全解,足见学生对于题目中的结构十分清晰。
变3的数据则较变1、2差一些,分析教学活动中学生的表现,不难解释,变3当中的两对“朋友数”被中间的“重复数”隔开了,要识别其中的结构,就需要学生有更自主的分辨能力。
学生既有了一定的解题技能,基于这种能力和层次的定位,我们安排本环节的拓展,着重在几个变形数阵形式的识别和比较中,强化对于数阵结构的识别。
【设计意图:在数据分析的过程中,可以很清晰地看到,前测中0组答案(全错)的学生占比高达61.8%,得到1组答案的占22.4%,2组答案的占5.3%,3组答案(全解)的占10.5%。经过教学,再进行变1、变2、变3的自主练习,数据发生了明显变化。】
四、课堂总结
师:今天我们观察了很多数阵,你发现这些数阵有什么共同点了吗?
生:每个数阵里都有重复数、朋友数。
生:朋友数的和相等,数阵就会相等。
生:这些数阵的答案都一样,只是换了个形状。
生:填这些数阵就是在填和相等的式子。
……
师:原来大家都发现了,数阵就是在“换衣服”,但是不管怎么换,聪明的同学仔细观察,就能找到藏在里面的朋友数和重复数。
【设计意图:本环节安排了三个不同的数阵,通过“换衣服”这种儿童生活中常见的经验,自然地引发学生对寻找重复数、朋友数的意义的思考,从而揭示数阵形状变化中的不变的结构特征“和相等”。】

