基于GA-BP神经网络算法的高精确度电阻测量系统

张文旭,梁继然,许延雷

(天津大学微电子学院,天津 300072)

在工业生产过程中,许多大型设备在运行中都需要监测温度、压力等参数,而常用的监测温度的方案大都采取PT100、PT1000热电阻,测量压力时通常采用压敏电阻,测量系统需检测这些敏感电阻的阻值以达到检测温度、压力等参数的目的[1-3]。目前测量热电阻与压敏电阻的外电路设计大致可分为惠斯通电桥电路以及恒流偏置电路两种。对于惠斯通电桥电路而言,其存在许多电路噪声,需要设计复杂的滤波电路降低系统噪声;对于横流偏置电路,需要设计高精度的横流偏置源。基于这两种硬件电路结构设计的系统,在算法上一般采取拟合的方式进行,但是环境温度或压力的变化与电阻的变化关系较为复杂,所采取的拟合函数往往普适性较差,同时一些硬件电路的噪声也会对电阻测量值产生一定的影响,这导致拟合结果偏离实际值。

国内有许多学者研究解决这一问题,其中魏光华等人采用五点标准模型进行最小二乘法的拟合[4],得到了较为精确的测量结果,但其测量结果中有些测量值误差较大,稳定性欠佳。邓翔宇等人采用分段线性拟合的方法解决了一些硬件电路的噪声也会对电阻测量值产生一定的影响[5],但是分段线性拟合的计算复杂度过大,算法需要的参数过多。田伟等人提出采用牛顿插值算法来解决桥式电路因温度变化所带来的误差[6],得到了误差不超过0.2%的测量结果,但这一做法仅能解决温度对传感器产生的影响。张邦成等人采用贝叶斯融合的方法解决传感器引入的噪声问题[7],其采用多个传感器数据进行融合,得到最终较为精确的测量结果,但其运算过程包含了积分与矩阵的运算,不利于应用在嵌入式系统中。

本文提出一种基于遗传算法(Genetic Algorithm,GA)优化的BP(Back Propagation,BP)神经网络算法,BP神经网络是一种按照误差反向传播训练的一种前馈网络,其主要应用在数据拟合、函数逼近等方面[8-9]。但BP神经网络存在学习速率慢、易陷入局部最小值等不足[10-11]。遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的一种计算模型,它通过模拟自然进化过程搜索得到最优解[12-13]。在BP网络训练参数之前,可以利用GA算法优化BP神经网络存在的不足。利用本文设计的系统测得GA-BP算法的训练集数据,先通过GA算法,迭代得到一个较为精确的全局最优解,再通过BP神经网络训练得到模型的最优解,再将得到的网络参数固化到单片机上,通过嵌入式系统可直接测得高精确度的电阻值。

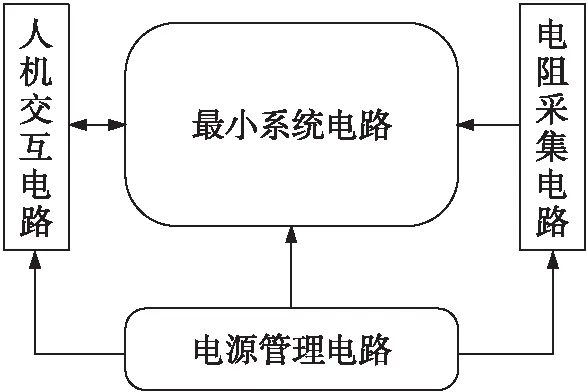
图1 系统原理图

1 系统硬件设计

本文提出的高精确度电阻测量系统主要由以下4个部分组成:最小系统电路,人机交互电路,电源管理电路,电阻阻值采集电路。其中最小系统电路采用ST公司的STM32F407芯片作为整个系统的主控芯片,该芯片具有高精度的12位ADC可以直接采集电阻采集电路的输出电压,得到精度为1 mV的模拟电压值。同时该芯片内部集成了浮点运算单元,可以加速浮点运算。人机交互电路采用的是0.96寸的OLED显示屏,其具有128×64的分辨率,可以实现字符与数字的显示;此外,采取旋转编码器与独立按键相结合的方式实现用户与系统间的信息交互。电源管理电路采用的是LM2596将外部输入的电压降至5 V,采用TPS7333线性稳压芯片将5 V电压降至3.3 V为整个系统的各个模块供电。

1.1 电阻阻值采集电路的设计

电阻阻值采集电路采用单臂惠斯通电桥结构,如图2所示,整个硬件设计上没有采用额外的滤波电路或复杂的设计。R3为可变电阻,这里参考PT1000的阻值变化范围选取R3的值为0.6 kΩ～1.8 kΩ,按照标准的电桥电路的输出电压表达式计算,电桥的输出电压的范围为30 mV～80 mV之间,为了能够提升单片机采集信号时的信噪比,需要将这部分输出的电压信号进行放大处理,进而有效地增大信噪比。STM32F407单片机自带的AD转换功能可以识别最大3.3 V的电压信号,因此需要将电桥输出部分的信号放大40倍左右,此处选择R5=31 kΩ。为此,选用AD623高精度仪器放大器作为放大电路的芯片,AD623芯片在工程设计上应用广泛,具有较宽的增益调节范围(1～1 000),可以满足本设计的要求。

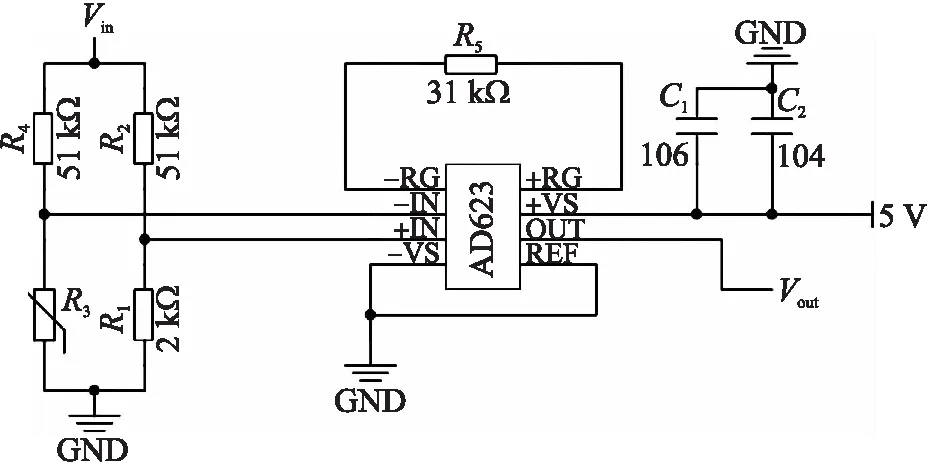
图2 电阻阻值采集电路

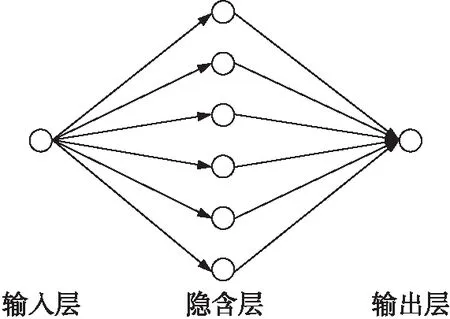
图3 BP神经网络结构

2 GA-BP神经网络算法

2.1 BP神经网络算法

BP神经网络算法是一种前向传播类型的神经网络,它具有三层或三层以上的网络结构,每一层都由若干个神经元组成,层与层之间的神经元采取的连接方式是全连接,即每一个神经元都与下一层的所有神经元进行连接。BP神经网络的主要用途之一是非线性函数拟合,它能够通过给定的数据进行计算,按照减小期望输出与实际输出误差的原则,逐步来调整网络参数,使网络实现对给定数据非线性的函数拟合。本文所应用的BP神经网络的结构如图3所示。

在惠斯通电桥模型中,我们可以把输出的电压和输入电阻的变化看作一种函数关系。经过推导虽然可以得到一个精确的函数关系,但是由于电路中存在一定的噪声,这使得得到的精确的函数关系中一些物理量的实际值与测量值之间发生了偏离,这使得我们依据推导出的函数关系所得到的测量结果存在着一定的误差。采取BP神经网络进行函数拟合的方法,可以将电路产生的噪声拟合在非线性的函数关系之中,从而得到更低误差的测量结果。

但是,BP神经网络存在一定的缺陷,利用BP神经网络进行训练的过程中,其训练时间过长,而且容易陷入局部最小值,导致训练缓慢,加大迭代次数。针对这一问题,本文采用遗传算法,对于BP神经网络训练过程进行优化,以减小训练时间与迭代次数。

2.2 GA优化算法

GA是一种通过模拟自然进化过程搜索最优解的方法。本文所采取的算法的思路是,开始随机产生n个种群,共经历N次迭代,每次迭代的过程中都会对每个种群的染色体编码的数值进行解码操作,得到对应的神经网络的参数值,根据神经网络输出Tout与给定数据O作比较,利用二者的二范数计算每个种群的适应度F,其计算公式为:

F=‖Tout-O‖2

然后按照适应度的计算结果生成每一个种群被选中的概率,接下来按照每个种群概率的大小随机选择两个种群,每个种群的适应度越大被选上的概率越大。被选中的种群会产生新的种群,同时,新种群会产生随机性的变异。GA算法的优势是,在迭代过程中不会陷入局部最优解,可以在全局上寻找最优解,但是GA算法迭代得到的解,会在最优解附近震荡,很难得到一个精确的最优解。

2.3 GA-BP算法

由于GA算法不能够精确地得到最优解,但是可以通过迭代得到最优解附近的解;BP神经网络在训练过程中容易陷入局部最优解,但是可以得到比较精确的解,因此本文将两种算法结合在一起,首先使用GA算法得到一个较为精确的全局最优解,然后再进行BP神经网络的训练,从而得到全局最优解,本文设计的GA-BP神经网络算法在MATLAB上实现,该部分的具体算法流程如下:①导入预先测量的数据,将数据分为训练集和测试集,并对数据进行归一化处理。②随机产生n个种群,每个种群的染色体编码采取浮点数编码,编码的染色体个数为19个,其中前6个表示输入层到隐含层的权重,第7～12个表示隐含层到输出层的权重,第13～18表示输入层到隐含层的偏置,第19表示隐含层到输出层的偏置。③计算n个样本的适应度,得到n个样本能够进行繁殖的概率。④按照每个样本可以繁殖的概率,挑选2个作为亲本,随机交换两个亲本的染色体得到新的子代。⑤重复n次步骤4,得到新的子代。⑥对子代的染色体进行变异,即随机增加一个(-0.09,0.09)之间的随机数。⑦重复N次步骤2-步骤6,即进行遗传算法的N次迭代,得到GA算法运行结束的近似全局最优解。⑧建立一个BP神经网络,该网络的输入层、隐含层、输出层神经元个数分别为1个,6个,1个,输入层到隐含层的激活函数为tansig,隐含层到输出层的激活函数为sigmod,将步骤7中得到的网络参数作为BP神经网络的初始化参数。⑨设定学习率lr,目标精度e,开始训练BP神经网络。⑩得到最优解的网络参数。

2.4 阻值测量系统软件程序

在程序的设计上,整个系统的软件架构是以u/COS Ⅲ实时操作系统为核心。采用嵌入式实时操作系统可以更合理、更有效地利用CPU的资源[14-15],简化应用程序的设计逻辑与各任务之间的外在联系,同时可以更好地保证系统的实时性和程序运行的可靠性。本文将步骤10中得到的网络训练参数直接用于STM32系统的软件设计部分中,STM32内部拥有浮点运算加速器,可以对指数函数运算进行加速。

图4 系统实物图

3 电阻测量试验与结果分析

3.1 电阻测量模型训练

本文所设计的系统实物图如图4所示,利用该系统所测得的模拟电压值与电阻阻值作为神经网络的训练数据。

为了得到使整个网络性能优良的种群个数n与迭代次数N,本文通过多次预训练实验,在训练实验中,选取迭代次数N=500,从图5中可以看出,迭代次数在100之后,虽然适应度有提高,但是提高的数值变化不大,初步选取迭代次数N=100,选取种群个数n=50。从图6中可以看出GA算法在迭代次数达到60次左右时,均方误差的值就稳定在0.063附近,每一次迭代中适应度最大的值会有阶跃式的变化,在第70次迭代后趋于稳定,适应度的最大值趋于16。

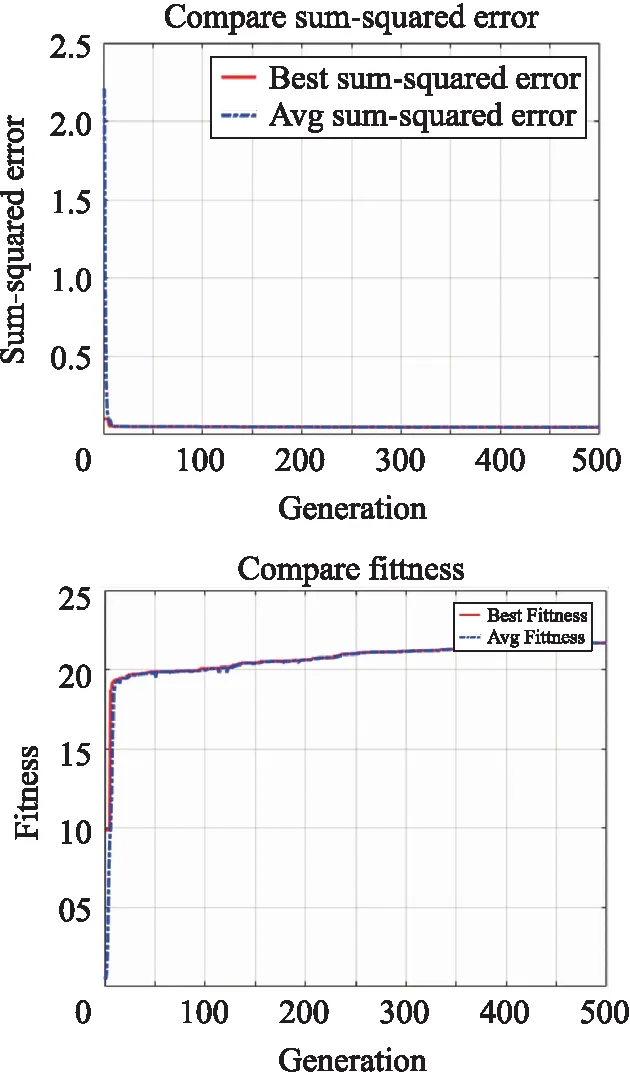
图5 预训练时GA算法每次迭代的均方误差与适应度

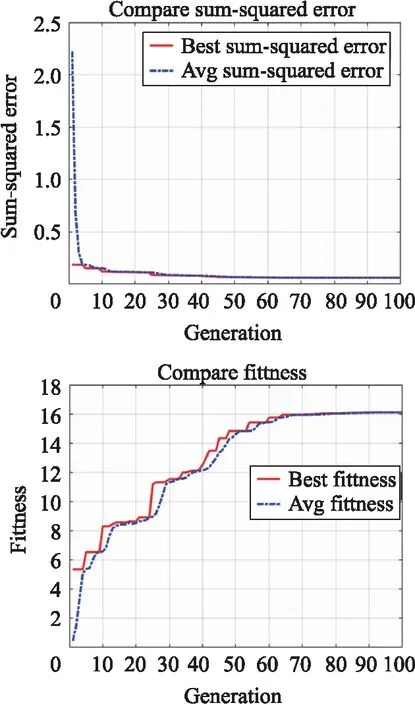
图6 n=50,N=100时GA算法每次迭代的均方误差与适应度

将GA算法计算得到的近似全局最优权重赋给神经网络,设定学习率lr=0.01,目标精度e=10-7,得到的训练结果如图7所示,从结果中可以看出在725次迭代后,整个网络的性能达到9.98×10-8,其网络训练的相关性系数R=1,从图8所示的拟合效果中可以看出,预训练的数据均匀的分布在光滑的拟合曲线上,训练效果良好。

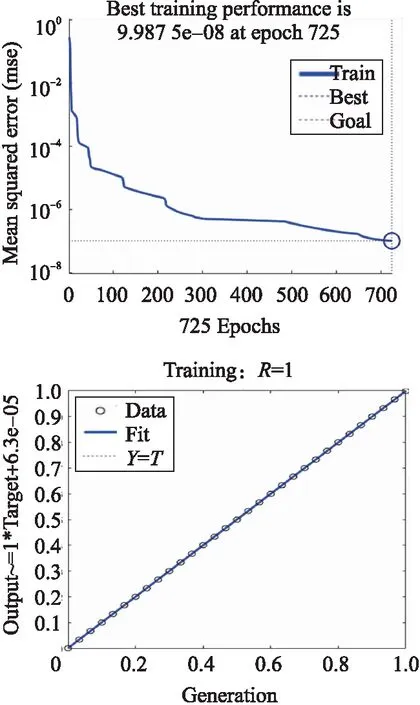
图7 网络性能结果

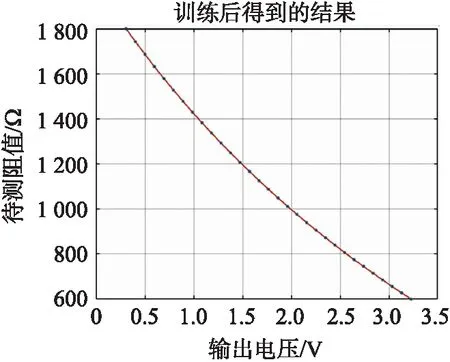
图8 非线性拟合结果

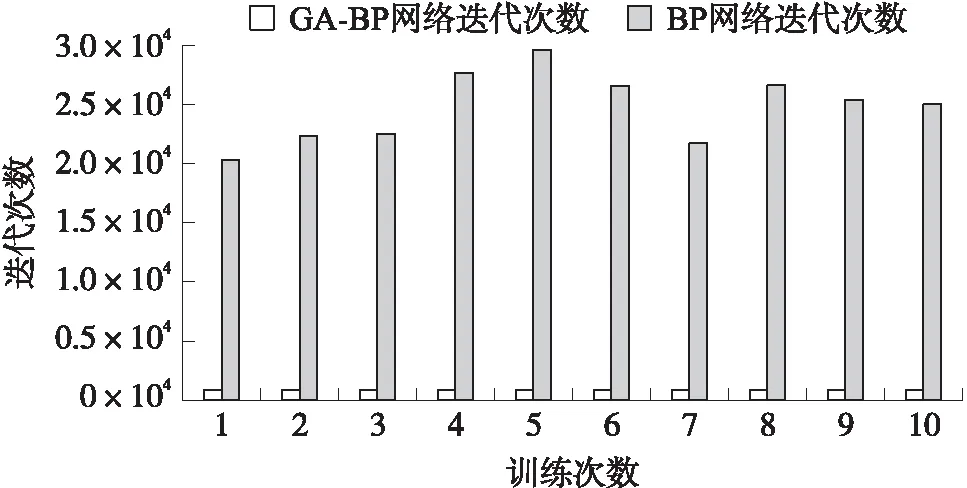
图9 GA-BP网络与BP网络迭代次数比较

利用GA-BP算法训练网络,记录10次训练结果,与未进行GA算法优化的结果进行对比,如图9所示。从结果中看出,GA-BP神经网络训练的迭代次数约为1 000次左右,而未使用GA优化算法的BP神经网络在训练过程中的迭代次数为20 000次以上,可以看出GA-BP神经网络算法在训练过程中迭代次数有明显的降低。

将训练好的GA-BP神经网络使用测试集验证网络的性能,得到的结果如图10所示,其测量误差大部分分布在0.1%以下,网络的性能较好。

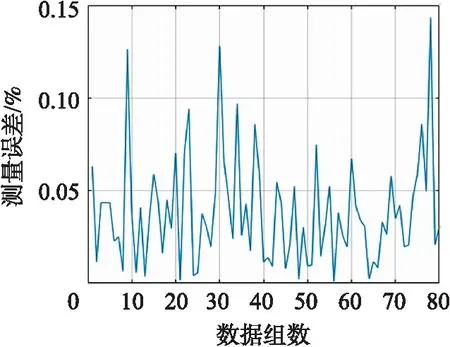
图10 GA-BP网络测试集相对误差

训练得到的网络参数如表1所示。

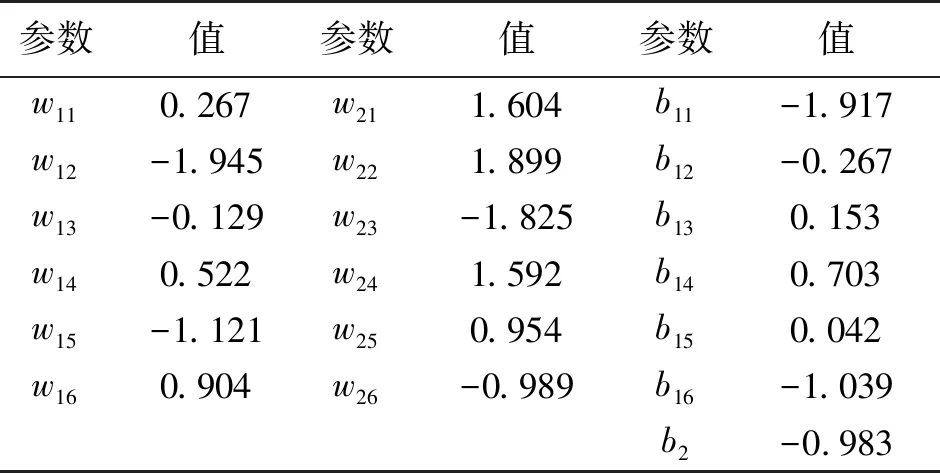
表1 网络参数训练结果

3.2 电阻测量试验结果

表2中随机测量了5组输入电阻和输出模拟电压的数据,分别利用理论公式计算、线性拟合、GA-BP神经网络得到以下测量结果,从结果中可以看出,相比于线性拟合的方法,GA-BP算法进一步降低了测量误差,GA-BP算法的测量误差约在0.1%左右。

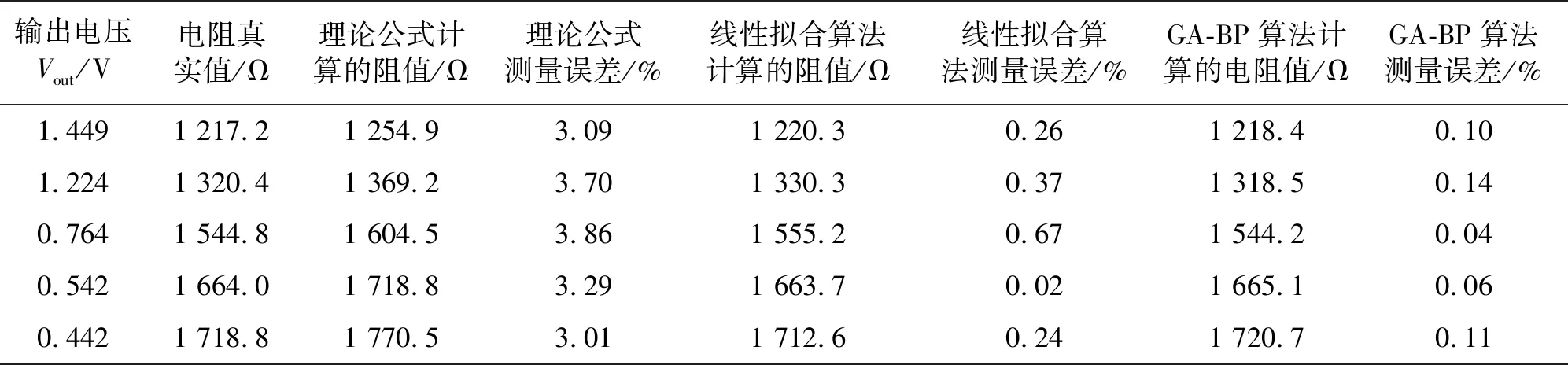
表2 理论公式计算、线性拟合、GA-BP神经网络对比

4 结论

本文提出了一种高精确度电阻测量系统,该系统根据预先测量的电阻与电压数据,训练神经网络,将网络输出作为测量结果。相比于传统的线性拟合算法,采用神经网络算法能够得到更为精确的电阻测量结果,实验结果表明,神经网络算法的电阻测量误差为0.1%左右。利用GA算法对BP神经网络进行优化,大大降低了BP神经网络训练过程中的迭代次数,可以加速网络的训练。此外本算法可以将神经网络算法实现的流程放到MCU上运行,直接在电阻测量系统上得到高精确度的测量结果,能为采用电桥电路的相关设计提供一定的参考。