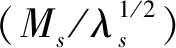磁致伸缩力传感器输出特性及其影响因素分析*
崔鑫鑫,王博文*,李明明,翁 玲,黄文美
(1.省部共建电工装备可靠性与智能化国家重点实验室,河北工业大学,天津 300130;2.河北省电磁场与电器可靠性重点实验室,河北工业大学,天津 300130)
磁致伸缩材料作为一种特殊的功能材料[1-2],可以实现机械能与电磁能的转换。其中,Fe-Ga与Fe-Co磁致伸缩材料响应速度快,磁机耦合系数高,具有良好的力学性能[3-4],可广泛应用于能量采集器[5]、执行器[6]和传感器[7]的核心元件。
逆磁致伸缩效应是指在给定的磁场强度下,磁致伸缩材料受到应力的作用时,材料内部的磁化强度会发生变化的现象[8]。应用磁致伸缩材料的这种特性可以制作各种传感器。贾振元[9]等利用坡莫合金棒的逆磁致伸缩效应设计了一种力传感器,可以实现静态和动态压力的测量,但没有分析出磁致伸缩对力传感器输出电压的影响。文献[10]通过实验验证了片状铁镓合金具有良好的扭矩传感特性,且输出信号具有较好的线性度。张露予[11]等通过实验研究设计了一种铁镓波导丝位移传感器,具有较大的量程和高的测量精度。文献[12]发现应用铁镓复合材料可以制作具有触觉感知的磁致伸缩传感器,输出电压可达240 mV。但磁致伸缩力传感器的输出电压与传感器核心材料的磁特性之间的关系仍不清楚,难于从物理机制层面上分析磁致伸缩力传感器输出电压的影响因素。本文采用片状Fe-Ga和Fe-Co材料,设计了一种悬臂梁结构力传感器,研究了力传感器的输出特性,并通过实验进行了验证。分析了力传感器输出电压的影响因素,确定了力传感器的输出电压与外力、偏置磁场及磁致伸缩的关系。

图1 磁致伸缩力传感器结构
1 磁致伸缩力传感器的结构设计
根据逆磁致伸缩效应和文献[13]的研究结果,设计了一种新型的类人指节的力传感器,力传感器的直径为8 mm、高为35 mm。力传感器主要由片状磁致伸缩材料、线圈、硬质触头、霍尔元件、骨架和硅胶外壳构成,结构如图1所示。实验中采用外力调节装置、直流电源和示波器构成的力传感器输出特性测试平台,测试设计的力传感器输出电压。测试过程为,直流电源为力传感器中的线圈提供电流,线圈在力传感器的片状磁致伸缩材料中产生大小可调的偏置磁场;外力调节装置为传感器提供大小可调的外力;传感器的霍尔芯片用来测量片状磁致伸缩材料底部固定端的磁感应强度,获得传感器的输出信号;通过示波器显示传感器受力时的输出电压值。为保证测量结果的可靠性,进行三次测量取其平均值作为输出电压值。
2 磁致伸缩力传感器的输出特性
由霍尔效应可得力传感器的霍尔输出电压为
U=KheKcdB=KheKcdμ0(H+M)
(1)
式中:Khe为霍尔系数,Kcd为磁感应强度传递系数,μ0为真空磁导率,磁感应强度B、偏置磁场H和磁化强度M均沿悬臂梁轴线方向。
考虑Dapino等人在文献[14]中提出的模型,在理想条件下无磁滞磁化强度M可表示为:
(2)
式中:He为沿悬臂梁轴线方向的有效磁场强度,a为无磁滞磁化强度M的形状系数,Ms为样品轴向的饱和磁化强度。
基于JA模型,有效场He可表示为
He=H+αM+Hσ
(3)
式中
(4)
式中:H为偏置磁场,α为磁畴作用系数,σ为悬臂梁所受轴向应力,Hσ为等效应力场,λ为悬臂梁轴向的磁致伸缩。
由二次畴转理论可得
(5)
式中:Ms为沿样品轴向的饱和磁化强度,λs为片状样品沿轴向的饱和磁致伸缩系数。
当传感器受到较小的垂直于样品轴向外力作用时,挠度很小,所受应力方向为样品轴线方向。此时片状样品受力遵循欧拉-伯努利悬臂梁理论,对传感器所选用磁致伸缩样品建立如图1所示的坐标系,并对其受力分析,则悬臂梁所受轴向平均应力与外力数值关系为
(6)
式中:I=wl3/12为悬臂梁的截面惯性转矩,l、w、h分别为0.45 mm、4.7 mm和30 mm。
经过计算得悬臂梁轴向平均应力与垂直样品轴向外力之间的大小关系为σave=4.34×105F。令σave=nF,则n=4.34×105Pa/N。
由式(2)~式(6)可得样品轴向磁化强度为
(7)
由式(1)和式(7)得霍尔输出电压为

(8)
取外力为零时的霍尔元件输出电压Ur作为参考电压,则传感器的输出电压模型为
(9)
对式(9)进行合并化简整理得
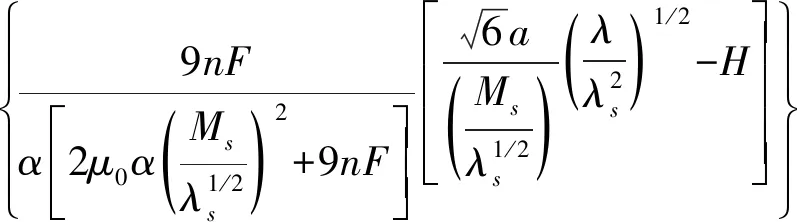
(10)
由式(10)可以看出力传感器的输出电压主要由偏置磁场、外力、λ/λs确定,并受Ms、λs、μ0、Khe、Kcd、a、α、和n的影响,其中Ms、λs、μ0可由文献[15]确定;Khe可由霍尔元件的型号确定;Kcd、a和α可由实验确定;n可由轴向应力与外力的关系计算得出。根据文献[15]和图2中的实验得到参数值列于表1。

表1 力传感器的模型参数
对于同一种磁致伸缩材料,当偏置磁场一定时,忽略外力对磁致伸缩的影响,由式(10)和表1的参数,可以计算力传感器输出电压与外力的关系曲线。在偏置磁场为6 kA/m时,计算得到的核心材料为Fe-Ga与Fe-Co力传感器输出电压与外力关系曲线如图2所示。通过对传感器输出电压进行测试,得到实验结果一并示于图2。实验结果表明传感器的输出电压模型可以很好地描述传感器输出电压与外力之间的关系。
从图2中可以看出核心材料为Fe-Ga的力传感器输出电压随着外力的增加而增大。当外力不超过1.4 N时,核心材料为Fe-Ga的力传感器的输出电压与外力之间具有较好的线性关系;当外力超过1.4 N时,随着外力的增大输出电压增加缓慢,逐渐趋于饱和。当外力增加到 2 N时,核心材料为Fe-Ga的力传感器的输出电压最大为110 mV。

图2 偏置磁场为6 kA/m时磁致伸缩力传感器的输出电压U-外力F关系曲线
对于核心材料为Fe-Co的力传感器,外力不超过1.2 N时,力传感器的输出电压与外力之间线性度较高;当外力大于1.2 N时,输出电压变化缓慢,基本达到饱和。当外力达到2 N时,力传感器最大输出电压为55 mV。对比核心材料为Fe-Ga的力传感器和Fe-Co的力传感器,可以看出两种力传感器在0~1.2 N的外力范围内输出电压与外力之间都具有较好的线性度,核心材料为Fe-Ga的力传感器的灵敏度明显高于核心材料为Fe-Co的力传感器的灵敏度,核心材料为Fe-Ga的力传感器的灵敏度可以达到66.69 mV/N,核心材料为Fe-Co的力传感器的灵敏度为37.91 mV/N。

图3 不同偏置磁场作用下核心材料为Fe-Ga的力传感器的输出电压U-外力F关系曲线
3 影响传感器输出特性的因素
3.1 偏置磁场的影响
由式(10)和表1的参数,在不同的偏置磁场下,计算可以得到的核心材料为Fe-Ga的力传感器输出电压与外力的关系曲线,如图3所示。实验测试得到的结果一并示于图3。从图3可以看出,偏置磁场小于6 kA/m时,力传感器输出电压随着偏置磁场的增加而逐渐增大。当偏置磁场大于6 kA/m时,力传感器的输出电压随着偏置磁场的增加逐渐减小。对于核心材料为Fe-Co的力传感器,理论计算和实验测试得到的结果与核心材料为 Fe-Ga 的力传感器的结果是一致的。因此对于特定材料的磁致伸缩力传感器存在一个最佳偏置磁场,力传感器工作在最佳偏置磁场处,使得力传感器输出电压和灵敏度都取得最大值。
3.2 磁致伸缩(λ/λs)的影响
为了研究传感器核心材料磁致伸缩(λ/λs)对输出电压的影响,采用磁特性测试平台[16]对30.00 mm×4.70 mm×0.45 mm片状Fe83Ga17和Fe71Co29样品的磁致伸缩进行测试。测试平台主要由信号发生器、功率放大器、霍尔芯片、动态应变仪、数据采集卡和电脑构成。测试过程中霍尔芯片垂直置于测试样品的表面采集样品的磁场强度。动态应变仪采集紧贴测试样品表面应变片的应变值。数据采集卡将霍尔芯片和动态应变仪采集的数据传输到电脑,通过相应电脑程序得到的实验数据和曲线。

图4 片状样品磁致伸缩-磁场关系曲线

当偏置磁场为4 kA/m时,片状Fe-Ga和Fe-Co材料的磁致伸缩比值(λ/λs)分别为0.4和0.66;当偏置磁场为6 kA/m时,片状Fe-Ga和Fe-Co材料的磁致伸缩比值(λ/λs)都为0.77。表明偏置磁场较低时,材料的磁致伸缩比值(λ/λs)对力传感器的输出电压具有影响;偏置磁场较高时,材料的磁致伸缩比值(λ/λs)对力传感器的输出电压影响较小。
3.3 磁化强度与磁致伸缩比值的影响

3.4 霍尔元件的影响
磁致伸缩力传感器的输出电压在一定程度上也受霍尔元件的影响,对于不同的霍尔元件,量程和灵敏度会有不同,导致其霍尔系数不同,从而对磁致伸缩力传感器输出电压产生一定的影响。实验中采用的霍尔芯片型号为SS491B,量程为-6 mT~6 mT,灵敏度为420 mV/mT。具有较大的量程和测量精度,可以实现较大传感器电压的输出。
4 结论