基于随机森林和粒子群优化的SVR的混合气体分析方法研究*
李紫蕊,范书瑞,花中秋,夏克文,张 艳
(河北工业大学电子信息工程学院,天津市电子材料与器件重点实验室,天津 300401)
气敏传感阵列因具有低成本、低功耗、能够实现多元气体检测等优点在电子鼻系统和无线传感网等领域中应用广泛[1-2]。然而,气敏传感器具有交叉敏感性,单个传感器在多元气体环境中无法实现目标气体的检测[3]。
对于这一问题主要从传感器阵列的选择和模式识别两个方面来解决。刘文贞等人[4]将遗传算法优化的小波神经网络用于建立基于红外光谱的三组分气体定量分析模型中有效地解决了气体之间相互干扰的问题。陈寅生等人[5]提出基于KPCA与MRVM的二元混合气体成分识别算法,提高了二元混合气体成分识别的准确率。但KPCA需要选择合适的核函数与参数ξ,降低了训练效率。为此,奉轲等人[6]提出PCA(Principle Component Analysis,主成分分析)与BP神经网络相结合的方法,虽然PCA减少了信息的冗余度,但BP神经网络的结构依旧复杂。因此,需要一种识别准确率较高且模型复杂度较低的气体定性识别方法。在回归方法中SVR(Support Vector Regression,支持向量回归)表现出了优异的性能[7-8],然而其性能的优劣在很大程度上取决于超参数。在以前支持向量机应用于传感器阵列的工作中,都采用一种简单的网格搜索方法[9-10]来选择合适的超参数。这种技术遍历指定值参数的子空间来选择最优值。由于超参数的取值空间不受限制,在很多情况下可以取任意实数值,因此子空间的选择并不简单。
为了解决上述问题,本文提出一种基于随机森林和粒子群优化的SVR的混合气体分析方法,实现对混合气体的高准确率检测,解决SVR超参数选择的问题。
1 混合气体分析流程
本文提出的混合气体分析方法主要分为气体定性识别和气体定量分析两个部分,定性识别采用PCA和随机森林相结合的方法,定量分析采用粒子群优化的SVR进行分析。
基于PCA和随机森林的混合气体定性识别算法框图如图1所示。训练过程中,利用PCA对训练样本集进行特征提取,得到特征向量集,利用特征向量集训练随机森林,得到随机森林模型;测试过程中,利用PCA对测试样本集进行特征提取,得到特征向量,利用训练得到的随机森林模型进行定性识别,得到定性识别结果。
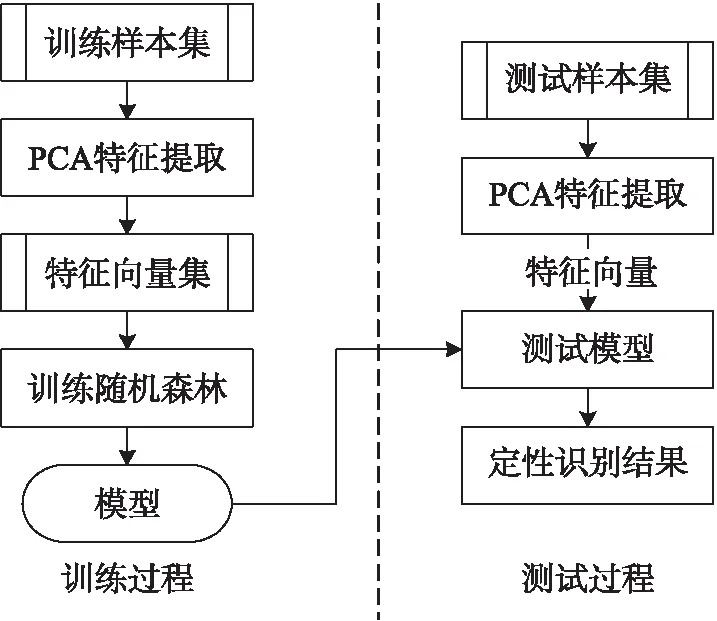
图1 混合气体定性识别方法
基于粒子群优化的SVR算法的混合气体定量分析方法框图如图2所示,整个过程分为训练过程和测试过程。训练过程中,用粒子群优化的SVR算法对训练样本集进行训练,获取最优超参数C和Gamma,然后保存最优模型;测试过程中,用训练得到的最优模型对测试样本集进行各成分的浓度估计。

图2 混合气体定量分析方法
2 混合气体定性识别
2.1 PCA特征提取
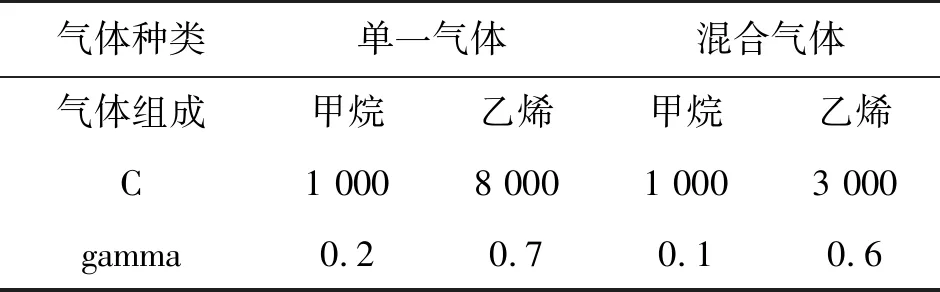
特征提取是模式识别和机器学习领域的基础和重要课题之一[11]。PCA是特征提取的一种方法,其基本思想是通过一组正交向量将原有特征(n个)变换为一组按照重要性从大到小依次排列的新特征(r个,r 假设X=[x1,x2,…,xM]∈RM×N为原始样本,其中,N为变量个数,M为样本个数,xi∈RN表示第i个N维样本。 (1) 用特征值分解方法求解协方差矩阵C(式(2))的特征值和特征向量,特征值从大到小排序为λ1,λ2,…,λN,对应的特征向量为α1,α2,…,αN。 (2) 最后通过特征值对方差的累计贡献率rCCR(式(3))确定要降的维数,rCCR≥95%时的p即为维数。 (3) 随机森林来源于决策树和bagging,决策树从给定的训练数据集中学习到一个模型用于对新示例进行分类。该算法需要两部分数据:用于构造决策机制的训练数据和用于验证所构造决策树的测试数据。决策树学习算法的流程如下: 随机森林在以决策树为基学习器构建bagging集成的基础上,进一步在决策树的训练过程中引入了随机属性选择。 粒子群优化算法通过群体中个体之间的协作和信息共享来寻找最优解[12],整个算法的流程如下: ①初始化一群微粒(群体规模为N)以及它们的速度和位置,设置最大迭代次数; ②定义适应度函数,评价每个微粒的适应度; ③个体极值为每个粒子找到的最优解,从这些最优解找到一个全局值,叫做本次全局最优解。与历史全局最优比较,进行更新; ④通过式(3)和式(4)更新粒子的速度和位置,其中,Vid和Xid为粒子i的d维速度和d维位置,Pid和Pgd为粒子i搜索的d维最优位置和整个种群的全局最优位置,ω为惯性因子,C1和C2为学习因子,random(0,1)为(0,1)之间的随机数; Vid=ωVid+C1random(0,1)(Pid-Xid)+C2random(0,1)(Pgd-Xid) (3) Xid=Xid+Vid (4) ⑤达到设定迭代次数时终止算法,未达到则返回步骤②继续执行。 SVR已被证明在化学传感器阵列的应用上比其他机器学习技术更准确。但超参数的选择往往耗费大量的时间,降低了整个算法的运行效率。因此,本文利用粒子群算法选择超参数C和gamma的最优组合,算法流程如图3所示。 图3 粒子群优化SVR算法 实验样本基于UCI数据集[13],该数据集由不同浓度的甲烷、乙烯、空气以及其混合物在16个传感器(TGS2600、TGS2602、TGS2610、TGS2620(每种类型有4个单元))的阵列下的响应组成,持续测量的时间为10 486 s。 为了更好地验证本文提出的混合气体分析方法,实验样本选择2 001~4 300 s的数据,在这段时间内气体类别有甲烷、乙烯、空气以及甲烷和乙烯的混合物。为了使实验结果更具有说服力,通过随机选取的方式划分训练集和测试集。 获取实验样本的传感器属于气敏传感器。气敏电阻的材料是金属氧化物,通常器件工作在空气中,空气中的氧和二氧化氮这样的电子兼容性大的气体接受来自半导体材料的电子而吸附负电荷,结果使N型半导体材料的表面空间电荷层区域的传导电子减少,使表面电导减小,从而使器件处于高阻状态。一旦元件与还原性气体接触,就会与吸附的氧发生反应,将被氧束缚的电子释放出来,敏感膜表面电导增加,使元件电阻减小。 为了探究获取实验样本的传感器对甲烷和乙烯的响应特性,以TGS2620传感器为例,观察其归一化响应以及对应时间段两种气体的浓度变化(为更加清楚地观察浓度变化,分别将两种气体的浓度进行了归一化)。分析图4可以看出,在前一个时间段内只出现一种气体(甲烷)的条件下,传感器的响应具有三个典型阶段:传感器首先暴露于干净的空气来达到基线水平,随后通入甲烷直到达到稳定的响应状态,当气体样本浓度降为0 ppm时,传感器恢复到基线水平;而在后一时间段内出现两种气体混合的情况,传感器的响应曲线不再像之前一样具有很明显的三个阶段。 图4 传感器响应曲线 经过以上分析可以得出,当所处环境中只有一种气体时,TGS系列的传感器具有稳定的响应;当有两种气体时,传感器具有交叉敏感性,这严重影响气体检测的准确性。我们并不能够直接根据原始数据准确地对混合气体进行定性识别,需要提取出包含有用信息的特征并结合合适的分类器才能解决传感器的交叉敏感性对气体识别带来的影响。 计算了16个特征值的贡献率及其累计贡献率,并绘制了各类别投影到前3个成分上的数据分数。由图5可看出,在前3个主成分下,各类别分别能够聚到一起,有助于进一步地定性识别。并且计算前3个特征值的累计贡献率达到了97.87%(超过95%),这证明前3个主成分能够大致代表所有的数据。原始的实验训练样本为1 840×16,测试样本为460×16,经过PCA进行特征提取后,特征训练样本为1 840×3,特征测试样本为460×3。 图5 前3个主成分的PCA得分图 实验数据可以分为4类:甲烷、乙烯、空气、甲烷和乙烯的混合物,将这些数据代入到随机森林分类中,得到4种类别的识别率。为了说明本文提出的PCA与随机森林相结合的定性识别方法的识别效果,下面将对随机森林(RF)、LogisticRegression(LR)和支持向量机(SVM)的识别效果进行比较。 本文用到的特征提取方法PCA属于线性特征提取,因此SVM的核函数选择‘linear’线性核函数,超参数C的选择集合为{0.1,1,10,100,1 000},SVM利用C的每一选择取值训练模型并进行测试,最后比较每一次测试集的识别精度。经过实验发现,5次测试集的识别精度相差不大,均在0.80~0.82范围内,因此选择识别精度最大值0.82对应的超参数C的值0.1。 表1给出了LR、SVM与RF3种分类方法对于4种气体类别的识别率和平均识别率,由表2可以看出随机森林在4种气体成分中的识别率最高,分别为0.96、0.98、0.95、0.94,平均识别率也最高为0.95。 表1 识别率和平均识别率 混合气体的定量分析需要在定性识别之后进行,对单一气体和混合气体分别利用粒子群优化的SVR进行浓度估计。 (3) 使用粒子群优化的SVR对于不同类别选择出的C和gamma值以及浓度估计结果如表2所示。 表2 不同类别的参数和浓度估计结果 为了说明本文提出的粒子群优化SVR(PSO+SVR)算法的有效性,下面将对比该算法与SVR的浓度估计结果。 (4) 取均方根误差RMSE最小时对应的超参数C和gamma组合,结果如表3所示。 表3 SVR预测各气体使用的参数 图6对比了PSO+SVR与SVR的浓度估计结果(横坐标的“1”、“2”、“3”、“4”分别对应甲烷、乙烯、混合气体中的甲烷、混合气体中的乙烯),从图5中可以看出PSO+SVR对所有气体类别的估计准确率均比SVR高10%以上。 图6 不同方法的浓度估计准确率对比 本文提出一种基于随机森林和粒子群优化的SVR的混合气体分析方法。该方法利用PCA进行特征提取,再利用随机森林实现定性识别,最后利用粒子群优化的SVR算法进行气体浓度的估计。通过与LogisticRegression和SVM的识别结果进行对比,证明了PCA与随机森林相结合的平均识别率最高达到了95%;粒子群优化的SVR对各气体类别的浓度估计准确率均比SVR高10%以上,证明了粒子群优化的SVR算法有较高的回归效果,有效地解决了SVR超参数选择困难的问题。
2.2 随机森林

3 混合气体定量分析
3.1 粒子群优化算法
3.2 粒子群优化的SVR算法

4 实验样本
4.1 实验样本组成
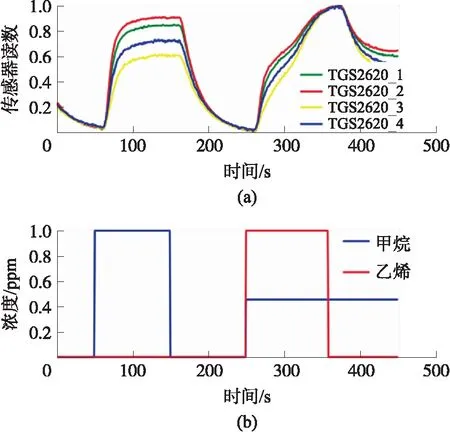
4.2 传感器响应特性分析
5 实验结果与分析
5.1 PCA特征提取

5.2 混合气体定性识别

5.3 混合气体定量分析




6 结论

