一种基于CSI的双人定位方法*
党小超,曹 渊,郝占军*,段 渝
(1.西北师范大学计算机科学与工程学院,兰州 730070;2.甘肃省物联网工程研究中心,兰州 730070)
室内多人定为在社会中具有极其重要的应用价值,目前主流的室内人员定位方法分为携带设备和非携带设备两大类,携带设备即被测目标身上携带特定的标签,研究者通过对标签的追踪来实现检测和定位,比较成熟的有使用超宽带(Ultra Wide Band,UWB)、RFID等等,但需要为每一位目标区域中的人员佩戴特定的设备,因此在成本花费以及使用灵活性方面存在一定劣势。非携带设备类型的研究主要依靠人体对Wi-Fi信号传播的影响,分为基于接收信号强度指示(Received Signal Strength Index,RSSI)信号和CSI信号两大类,RSSI提供的信息比较单一,而CSI信息能够更全面的反映Wi-Fi信号在传播过程中受到的影响,同时通过CSI进行人员检测的研究因为具有无需携带额外传感器、可扩展性强、不受温度、灯光、湿度等外界条件的影响等优点[1],成为当下研究的热点。
当前基于CSI进行定位的研究大多关注提高单人定位精度和优化算法方面,例如将CSI和RSSI进行融合的定位方法[2],相较于单一的使用CSI或者单一的使用RSSI的方法极大的提高了定位精度,但无法直接应用于多人的情况。文献[3]等人使用K-means 算法并且提取CSI矩阵中的多条向量作为特征,较好的提高了单人定位的精度,但面临数据量很大的情况时则识别效率比较低。文献[4]等人通过提取CSI数据的相位和幅值信息,在此基础上采用机器学习的方法进行一种无源的室内定位,一定程度上提高了定位精度,但同样没有进行多人定位方面的研究。文献[5]提出了一种基于CSI信号进行室内定位的FILA系统,在实验环境中取得了较高的准确性。文献[6]采取指纹库定位的思想,将深度学习的方法应用到室内定位中,提高了定位的精度。文献[7]中,作者用CSI中的相位信息建立指纹库,并采用深度学习的方法,使得定位精度进一步得到提升。文献[8]综合分析CSI的每一条子链路和每一条子载波的信息,综合起来进行室内定位,也取得了较好的定位精度。文献[9]使用神经网络的方法来进行室内定位,进一步的提升了室内定位的精度和性能。文献[10]提出了一种鲁棒性良好的室内定位方法,实验验证在不同的环境中确实表现良好,但只能针对单人的定位。文献[11]采用了改进的贝叶斯分类器进行室内定位,实验证明比基于传统的贝叶斯分类的室内定位方法的性能提高了至少15%。文献[12]提出了一种基于CSI信号的到达角和RSSI融合的室内定位方法,该方法的定位误差缩减到了0.7 m。文献[13]在5G环境下使用K-近邻的分类算法对室内定位进行了研究,提升了定位的准确性,但只能够定位一个人。文献[14]提出了一种随机森林指纹定位方法,降低了建立指纹库的复杂度。但就目前研究而言,关注双人以及多人定位的研究鲜有报道。鉴于当前基于CSI进行多人感知领域较为空缺的现状,本文提出一种基于CSI的双人分阶段定位方法。因为被测人员体型以及相互站位都对于CSI信号有着影响,因此当被检测人数上升时,需要建立的指纹库就会极其复杂,同时算法的复杂度也直线上升。例如,当监测点为8,被测人员数量为4时,共有163种情况[15],导致建立指纹库极为复杂。为了解决这一问题,本文提出一种分阶段定位的方法,第一步先使用K-means算法进行聚类,建立粗指纹库。第二步在粗指纹库的基础上使用SoftMax分类算法进行细致的分类,建立细指纹库。最后在实时匹配阶段,采集的数据需要先经过粗指纹库匹配得到粗定位结果,再经过细指纹库匹配,得到最终的定位结果。
1 理论与模型
1.1 CSI多人信号特征
随着802.11/n协议的使用,我们可以从符合此标准的商用Wi-Fi设备中提取出CSI信息。CSI信息体现Wi-Fi信号在每条传输路径上的衰减情况,具体而言是一个m×n×k的复数矩阵,其中m表示发送端天线的数量,n表示接收端天线的数量,k表示子载波的组数。
对于使用OFDM技术传输的信号,接收端的信号可以表示为:
Y=HX+N
(1)
式中:X和Y分别为信号在发送端和接收端的向量表示,其维数为M×1,H是信道状态信息矩阵,N表示高斯白噪声向量,其维数为M×1。每个子载波的CSI可以表示为:
H=Y/X
(2)
使用Atheros9380网卡以及修改LINUX内核驱动可以采集得到CSI数据。图1(a)、图1(b)分别表示在不同站位情况下采集的CSI数据振幅波形图,从图1中可以明显看出两者具有差别,即使用CSI进行多人检测和定位具有可行性。
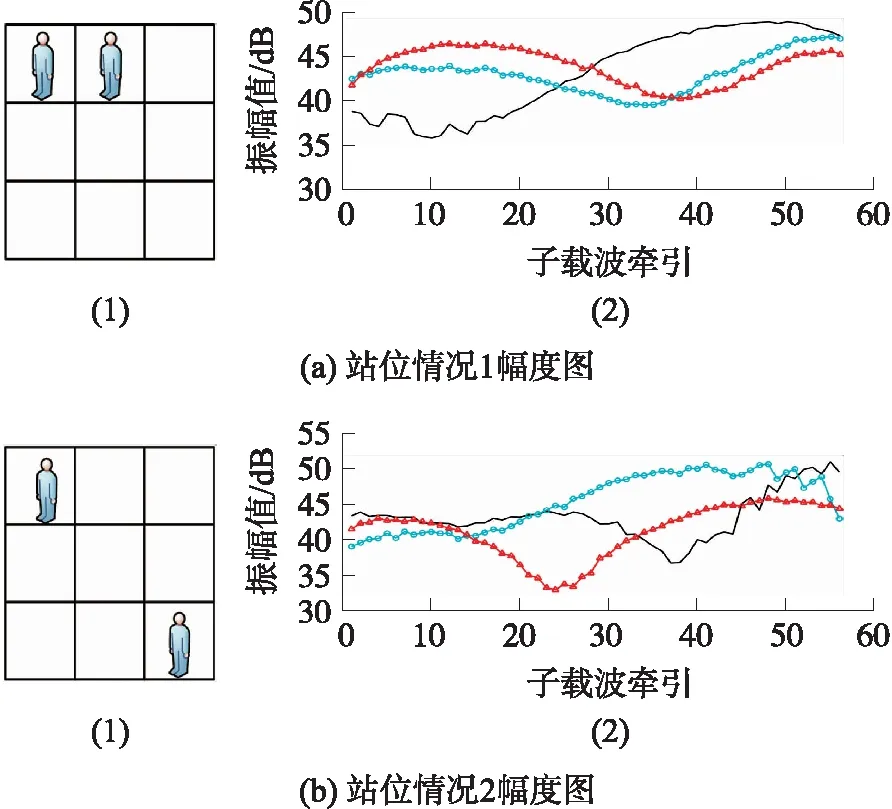
图1 CSI幅度图
1.2 多人检测方法
方法分为离线训练和在线匹配两个阶段。在离线阶段,对被检测区域中存在2个人的情况进行建模,并采集不同情况下各自的CSI信息,对所采集到的CSI数据进行降噪预处理,第一步粗分类对预处理后的数据使用K-means算法进行簇类回归,建立粗指纹库,在粗分类结果的基础上,再使用SoftMax分类算法进行每个簇类的细分类,建立细指纹库。在线匹配阶段先将采集到的数据进行与离线阶段同样的预处理过程,然后将其与粗指纹库进行匹配,得到粗定位结果,在得到粗定位结果的基础上,与细指纹库进行匹配,得到最终的定位结果。分两步进行匹配,极大的降低了建立指纹库和匹配算法的复杂度,系统的流程图如图2所示。
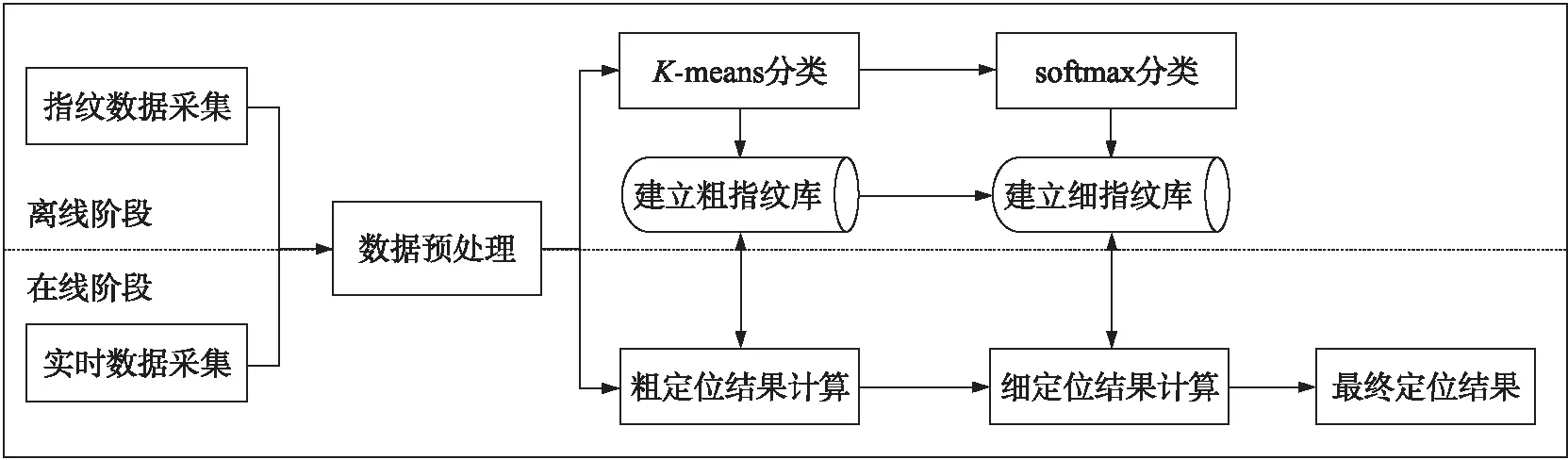
图2 定位方法流程图
1.3 箱型图模型
在CSI数据采集的过程中,因设备自身影响以及室内复杂实验环境的干扰,采集的数据会存在异常值,而异常值对系统模型的训练和分类具有较大的影响,因此需要对采集的数据先进行异常值处理。本文使用箱型图分析的方法来剔除异常值,箱型图是在采集得到的实际数据的基础上绘制的,能够真实的反映数据的真实情况,因此在异常值处理中具有一定的优越性,先将采集到数据中的中位数和上四分位数Q3和下四分位数Q1,再绘制成如图3箱型图处理示意图所示矩形图,取Q3+1.5IQR(IQR=Q3-Q1)处的值画一条与中位线平行的线段,定义为上内限,同理定义下内限为在Q1-1.5IQR处的线段。异常值定义为所有上内限之上和下内限之下的值,预处理过程完成对异常值的剔除。
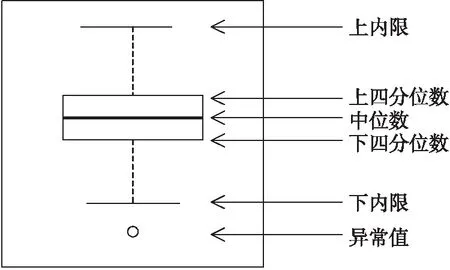
图3 箱型图处理示意图
2 算法描述
2.1 K-means粗聚类
本文提出的方法需要通过对采集到的数据进行K-means聚类回归,在回归得到的结果的基础上建立粗指纹库,从而完成粗分类的任务。因为通过Atheros9380网卡采集到的CSI数据都是2×3×56的矩阵,即共有6条子链路,为了便于描述,挑选其中的第i条用于本文方法的描述过程,其余子链路采用同样的处理方式。
Step 1 在采集所得的80%数据中,对于每一种站位情况提取50组数据,根据所选的第i条子链路,将50组数据中的第i条子链路进行加权平均,得到每一种站位情况下的MeanVi(i=1,2,3,…,36)。
Step 2 将上一步得到的36个幅值向量作为输入,选取k值进行K-means回归。
Step 3 经过第2步的回归,我们已经得到了初始36个类别和最终k个类别的映射关系,在此映射基础上建立粗指纹库,即我们得到k个质心作为标志,粗指纹库为Fin={F1,F2,F3,…,Fk}
2.2 SoftMax细分类
在2.1节建立粗指纹库的基础上,对每一个簇类下包含的双人站位情况,分别进行SoftMax分类,建立细指纹库fin={f11,f12,f13,…,fkn}其中,f11表示该指纹为第一簇类下的第一种站位情况。过程如下:
Step 1 将F1簇类下的各个数据作为分类器的输入,通过调整权值衰减系数λ的值,得到相应概率数值的输出。对于一种站位情况,从80%的数据中共训练得到m个指纹:Fijk(k=1,2,…,m)
Step 2 对上一步训练得到的m个指纹,取其平均值,得到fij:
(3)
2.3 实时匹配
在线阶段首先在采集不同测试点的CSI数据,首先进行同离线阶段一样的数据预处理,记处理后的CSI数据为TS。定位过程分为粗定位计算和细定位计算两个阶段,在粗定位计算阶段,通过采集到的CSI数据与粗指纹库Fin匹配,确定属于哪一种簇类,在粗定位结果的基础上,再将测试数据与细指纹库fin={f11,f12,f13,…,fkn}进行匹配,得到最终的定位结果。
2.3.1 粗定位结果计算
该过程中,通过计算TS与粗指纹库中各个指纹的欧几里得距离,与哪个聚类中心距离最为接近,则属于哪个聚类,得到粗定位结果。具体过程如下:
Step 1 计算处理后的CSI数据TS与粗指纹库Fin中每个指纹的欧几里得距离(同一条子链路),可以表示为:
(4)
式中:n表示粗指纹库的总数,Fi∈Fin,TSj表示采集到的测试CSI值中第j条子链路的幅值向量。
Step 2 将dij按值大小升序排序,选取最小的dij,得到对应的i值,则该测试数据属于粗指纹库的第i类,得到粗定位计算结果。
2.3.2 细定位结果的计算
在2.3.1节得到粗定位结果的基础上,继续计算TS与上一步已经分类得出的细指纹库fin的欧氏距离,通过比较,得到最终的定位结果,过程如下:
Step 1 计算TS与细指纹的欧几里得距离dstij如下:
(5)
式中:fij表示细指纹库fi中的某一个指纹,n为细指纹库的总数。
Step 2 将dstij的值按大小升序排序,选取最小的dstij,得到对应的i、j的值,则该测试数据属于细指纹库fij类,得到最终的定位结果。
3 实验与分析
3.1 实验环境
实验设备包括两个联想台式电脑,分别作为发射机和接收机,两台电脑的操作系统为Ubuntu16.04LTS,CPU型号均为Intel Corei3-4150,提取CSI数据使用Atheros9380网卡,且发射端和接收端代码均经过调制,能够调节不同的发包速率。为了验证本文提出的系统的性能,在实验室进行了验证实验。实验场地为3×3的正方形网格区域,每个格子的边长为0.80 m,实验室场地图及平面布局图如图4、图5所示。
主成分分析法应用于统计中的主成分分析,是将一组原始指标转换成具有相同趋势的新变量,计算出若干个主成分,再根据各主成分对研究对象的贡献率进行一定的线性组合,构造出综合主成分进行综合评分,然后根据综合评分的高低顺序进行排序,以达到综合评价的目的[31]。
在数据采集的过程中,两位被测者分别挑选任意的两个格子静止站立。两位被测者保持静止10 s,发包速率分别为20包/s、50包/s、100包/s,因此一个位置共采集200、500、1000个数据包,同一位置重复采集10次。采集到的数据80%用于离线阶段的训练,20%用来在线阶段的测试。

图4 实验场地图
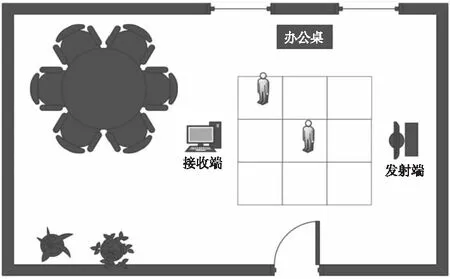
图5 实验室平面布局图
3.2 方法的性能分析
3.2.1 方法的识别率
本文定义方法的识别率为识别正确的样本数占总被测样本数的比例,正确识别两人分布站在几号定位格中且定位误差在1.20 m以内即被定义为识别正确的样本。
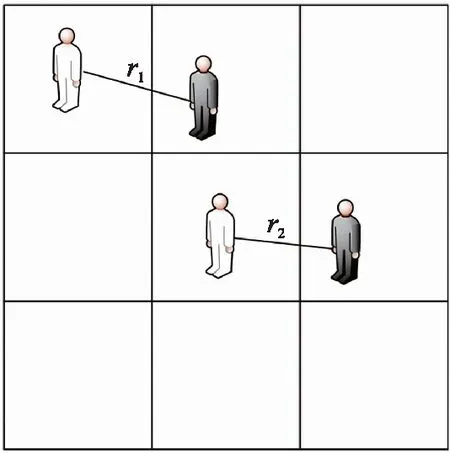
图6 定位误差定义图
3.2.2 定位误差
因本文是针对于双人的定位方法,特提出双人定位方法的定位误差计算方法,如图6所示,白色小人为实际的站位点,黑色小人为本文方法计算的位置点,其中r1和r2分别表示两个被测人员实际站位点跟方法定位点的距离。定义方法的定位误差为ED:
(6)
3.2.3 双人间距对识别率的影响
双人定位实验中,双人间距对于定位的误差必然存在影响,现有研究的定位精度一般都是在1.00 m以上,因此设定两人间距分别为0.40 m、0.80 m、1.00 m、1.20 m、1.60 m、2.40 m的不同情况下的对比实验,来研究双人间距对于定位误差的影响,实验结果如图7所示。
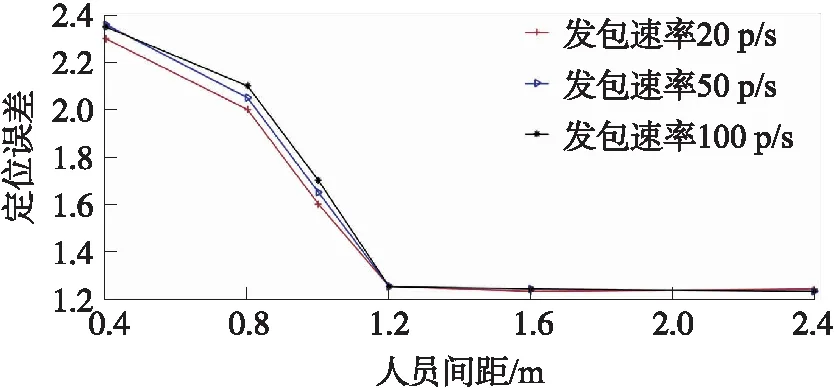
图7 人员间距对定位误差影响图
从图7可以看到,当人员间距在1.00 m以内时,定位误差平均在1.60 m以上,即定位误差较大。当双人间距为1.20 m时,定位误差为1.18 m。随着人员间距持续增大,定位误差并没有显著的减少。为了研究人员间距对站位关系识别率的影响,在同上所述的间距分布情况下进行了识别率的统计,统计结果如图8所示。
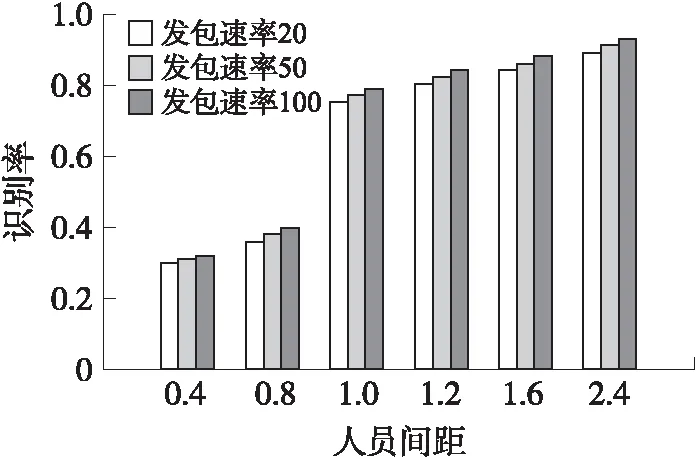
图8 人员间距对识别率的影响
从图 8可以得出,当双人间距小于1.00 m时,方法的识别率维持在50%左右,当双人间距在1.00 m以上时,方法的识别率平均在80%以上,随着人员间距的增大,识别率有少量的提高,最高达到91%。考虑到实验的可实施性以及均衡性,本文后续的实验,均是在双人站立间距为1.20 m的情况下进行的。
3.2.4 被测人员对系统的影响
因为基于CSI运用指纹库进行定位方法固有的局限性,当被测人员不同时,定位的精度和准确率有着明显的差别,因此为了研究被测人员固有的体型特征对本文提出的方法的定位精度和识别率的影响,特挑选不同的人员进行实验,实验人员有:
男1:身高185 cm 体重65 kg
男2:身高180 cm 体重68 kg
女1:身高170 cm 体重52 kg
女2:身高163 cm 体重45 kg
不同的组合分别有:A(男1,男2)、B(男1,女1)、C(男1,女2)、D(男2,女1)、E(男2,女2)、F(女1,女2)。

图9 被测人员实验图
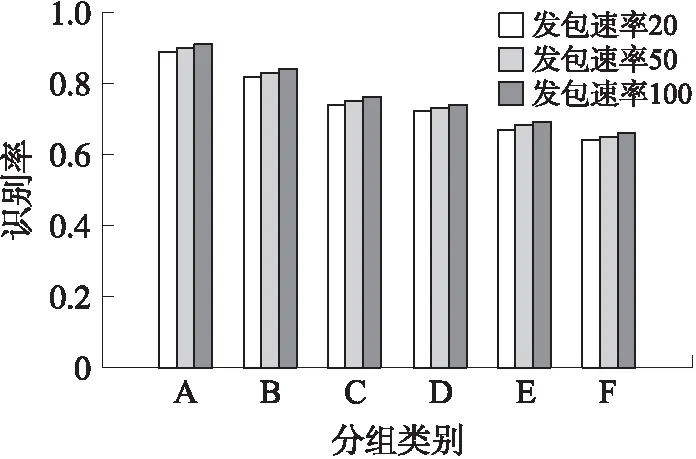
图10 被测人员对识别率影响图
由图10可以看出,在被测人员体型较为相似的情况下,来研究双人定位,识别率是较为好的,因为相似的体型相比于体型相差较大,减少了所测数据的复杂度,因此当数据用于特征提取和分类时,具有更好的效果。所以本文后续实验,均采取(男1,男2)组合。特此说明。
3.2.5 设备高度对于定位的影响
在基于CSI的定位中,发包的速率以及发射机和接收机的高度均对于定位的精度存在影响,因此对于接收机和发射机高度分别为0.50 m、1.00 m、1.50 m的情况下分别进行定位实验,研究设备高度对于定位误差和方法识别率的影响。设备高度对于定位误差的影响如表1所示。
分析表1可以得出,不同的设备高度对于定位误差存在较大的影响,当设备高度为1.0 m时,平均定位误差最小,达到1.08 m。统计不同设备高度下的识别率如图11所示。

表1 设备高度与定位误差关系表 单位:m
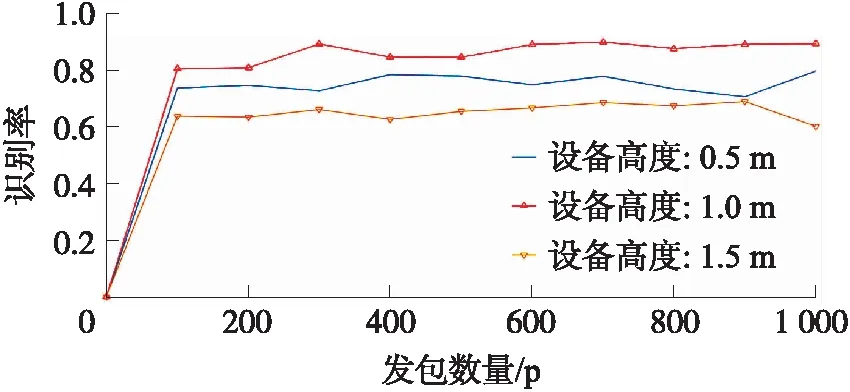
图11 设备高度对识别率影响图
从图11可以看出,设备高度对于双人定位的识别率存在一定的影响,当设备高度为1.00 m时,本文提出方法的识别率最高,可以达到90%左右。
3.2.6 发包速率和设备间距对识别率的影响
不同的设备间距对于双人定位问题可能存在不同的影响,为了研究得出最佳适合本文方法以及实验场景的设备间距,特在设备间距分别为3.00 m、4.00 m和5.00 m三种情况下进行实验。在不同的设备间距和不同的发包速率下,分别研究方法的定位误差和方法的识别率,表1为在测试样本为100个时,在不同发包速率以及不同设备间距下的识别率。
从表2中可以看出,设备之间的间距会影响定位识别的准确率,因为本实验场景设置的特殊性,在本文描述的实验场景下,当设备间距为3.00 m时系统的识别率高于其他情况,不同的发包速率对准确率具有一定的影响,当发包速率为100包/s,设备间距为3.00 m时,得到方法的最佳识别率91%。
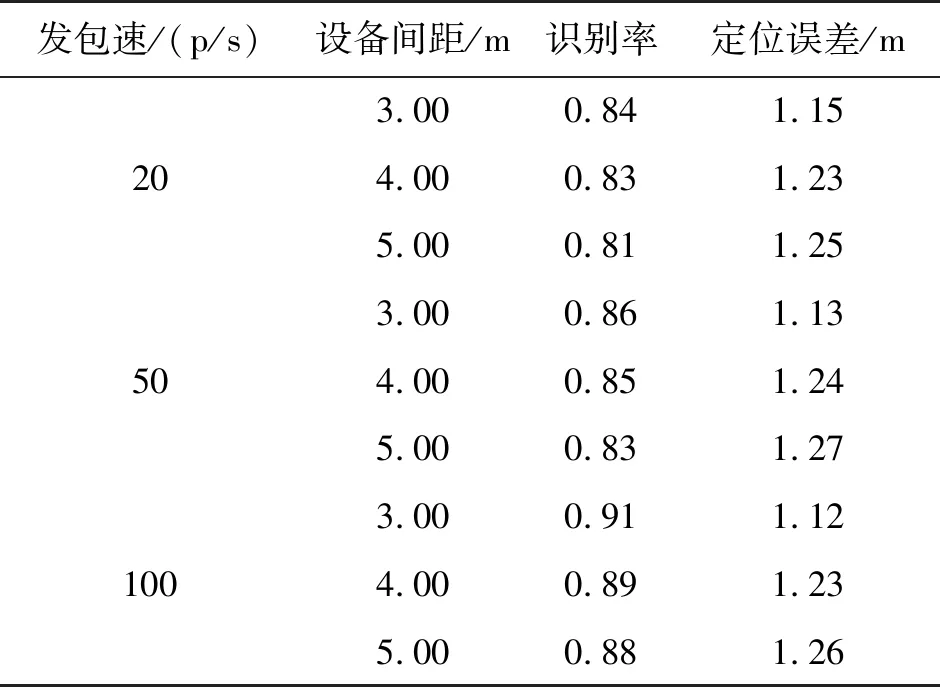
表2 设备间距与定位误差关系表
4 总结
本文提出了一种基于CSI的双人分阶段定位方法,通过粗定位和细定位两个过程确定了双人的站立点和站位关系。提出的方法经过实验验证后,最终的定位误差在1.00 m~1.20 m之间,站位关系识别率最佳为91%,较好的解决了基于CSI的定位随着人数上升引起的指纹库建立和匹配算法复杂的问题,本文将来会致力于研究更多人数的并发感知和并发检测方面。

