双向S-优势概率粗集的构造及应用

陶 志，王 丹

（中国民航大学理学院，天津 300300）

由波兰数学家Pawlak[1]提出的粗糙集理论，作为一种处理不确定性数据知识的新理论，已被广泛应用在知识发现、决策分析、数据挖掘、人工智能等领域[2]。在Pawlak工作的基础上，Shi[3]给出了动态粗集的描述，进而提出了S-粗集（singular rough sets）。但S-粗集没有充分利用知识分类过程中的统计信息，因而无法处理具有统计信息的不确定性动态系统中的知识分类问题。文献[4]提出的S-概率粗集模型能够处理动态统计信息，但该模型建立在等价关系基础上，其在含有偏序关系的动态多属性统计类决策问题中的应用受到了限制。因此，在文献[4]所提模型基础上将等价关系改为优势关系[5]，提出一种新的双向S-优势概率粗集模型，新模型使得S-粗集模型在一些特殊的信息决策领域有更广泛的应用，既是对S-粗集理论的扩充，同时也便于利用S-粗集理论在带有偏好信息的动态数据系统中进行数据挖掘，以便从相关决策系统中获取更合理的规则。最后，给出一个新模型在风险投资识别问题中的简单应用，说明新模型可有效应用于含有偏序关系并具有动态统计信息的不确定性决策领域。

1 基本知识

1.1 优势关系粗糙集

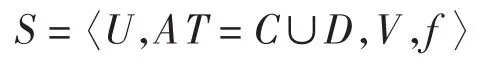
首先，引入基于优势（偏序）关系的粗糙集理论中的几个相关概念[6]。设有形式化的偏好决策系统为其中：U为非空有限论域；AT为非空有限属性集，分为条件属性集C和决策属性集D，C∩D=；V为属性值集，V=VC∪VD，VC为条件属性值集，VD为决策属性值集，且属性具有偏好次序；f：U×AT→V是一个信息函数，表示对每一个x∈U，q∈AT有（fx，q）∈V。

在偏好决策系统S中，依据决策属性集D可将U划分为有限个决策类集合：cl={clt|t∈T}，T={1，2，…，n}，通常认为决策属性划分的决策类集合是有序的，即∀r，s∈T，若 r＞s则clr里的对象从决策角度考虑优于cls里的对象。

定义1设S为偏好决策系统，clt为决策属性集D下的一个决策类，clt的向上累积集（clt的优势类）为向上累积集是由优于决策类clt的对象全体构成的集合。

定义2设S为偏好决策系统，C为条件属性集，若对于P⊆C和∀q∈P，总有x≥qy，则称x在条件属性集P上优于y，记为xDPy。对于给定的P⊆C和x∈U，称集合为属性集 P 关于 x的优势集。

定义3设S为偏好决策系统，属性集P⊆C，则向上累积集clt≥的下、上近似集分别为

1.2 双向S-优粗集基本概念

文献[7-10]对S-粗集给出详细描述，基于上述文献中关于S-粗集的描述，针对含有偏序关系的双向动态集合引进动态优势粗糙集的概念[11]如下：

在偏好决策系统S中，集合clt≥为决策类clt的向上累积集，F={f1，f2，…，fm}与是定义在 U 上的元素迁移族是元素迁移，代表 f（u）与集合clt≥之间满足以下关系：元素，在f∈F的作用下变成f（u）=x∈clt≥；而元素x∈clt≥在的作用下变成。

定义 4设 clt的向上累积集为，称U是U上的一个双向S-优势集合，如果。其中的亏集，且。

定义5设是U上的一个双向S-优势集合，称分别是双向S-优势集合的下、上近似，如果满足若，则称集合对〉是的双向S-优势关系粗集（简称双向S-优粗集）。

定义6称为双向S-优势集合的 DP近似精度，（|·|表示集合的基数）；称为双向S-优势集合的 DP粗糙度。

2 双向S-优势概率粗集

双向S-优粗集在分类过程中没有考虑知识分类中对象优势集的统计信息，存在由其“刚性”特质所决定的固有局限性，如对扰动（噪声）数据过于敏感等。为此，提出双向S-优势概率粗集模型，新模型具有某种“柔性”特征，因而增强了数据分析和处理的鲁棒性。

定义7设是U上的双向S-优势集合，Γ=F∪，P为定义在U上的子集类构成的σ代数上的概率测度，则依参数α的下、上近似集分别为

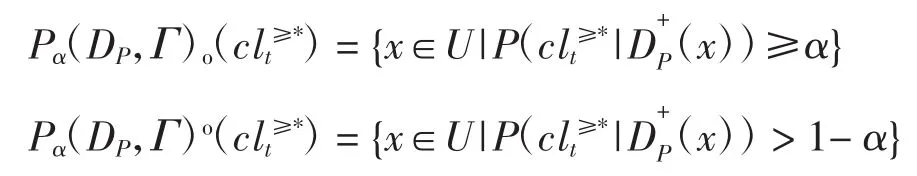
定义8设是U上的双向S-优势集合，则依参数α的双向优势概率粗集的正域、负域、边界域分别为

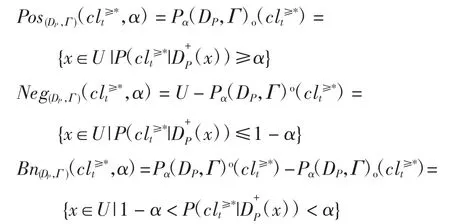
定义9称为双向S-优势集合的DP概率近似精度；称为双向S-优势集合的DP概率粗糙度。

3 双向S-优势概率粗集模型的性质

利用概率相关性质和定义7分析可知，双向S-优势概率粗集有如下性质。

性质1设0.5＜α≤1，则

性质2

性质3设存在元素迁移Γ使分别变为双向 S-优势集合，则对任意0.5＜α≤1，恒有：

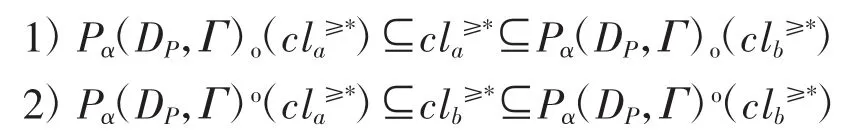
证明设，由于，有α，故有，即x∈Pb（DP，Γ）o（）。故1）得证，同理可证2）亦成立。

性质3 表明，对已确定优势关系的两个决策类，其粗糙上、下近似集合在任意α概率水平上仍保持其优势关系不变。

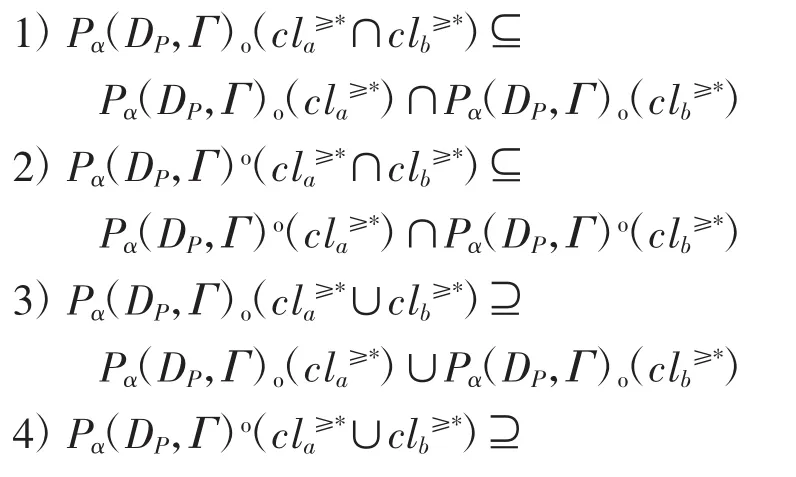
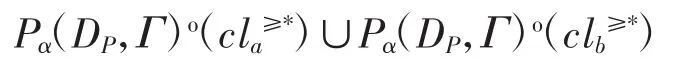
证明由及性质 3 易证 1）～4）成立，略。

性质 5设 0.5＜ α1≤α2≤1，则有：

证明设，即，由于 α1≤α2，有成立，即，故1）得证。同理可证2）亦成立。

由上述性质及相关定义可得到如下结论。

定理1当α=1时，有：

定理1说明，当α=1时，双向S-优势概率粗集退化为双向S-优粗集。

推论1若有限论域U上的任意两元素关于属性集AT由优势关系退化为等价关系时，则双向S-优势概率粗集即退化为双向S-概率粗集。

推论2若有限论域U上的任意两元素关于属性集AT由优势关系退化为等价关系且Γ=时，则双向S-优势概率粗集即退化为Pawlak意义下的概率粗集。

推论3若有限论域U上的任意两元素关于属性集AT由优势关系退化为等价关系且Γ=，α=1时，则双向S-优势概率粗集即退化为Pawlak经典粗集。

定理2设0.5＜α≤1，则：

1）Pd(DP，Γ)（，α）≥d(DP，Γ)（）

2）Pρ(DP，Γ)（，α）≤ρ(DP，Γ)（）

推论4设0.5＜α≤1，则

定理2和推论4说明，双向S-优势概率粗集比双向S-优粗集的近似精度增加了，而不确定性（粗糙）边界减小了。进一步分析可知，当α趋于极限值0.5时，近似集合之间有如下关系。

定理3设0.5＜α≤1，则当α→0.5时，有：

1）Pα→0.5（DQ，Γ）o（）=∪Pα（DQ，Γ）o（）；

2）Pα→0.5（DQ，Γ）o（）=∩Pα（DQ，Γ）o（）。

上述定理给出了动态决策（优势）集在0.5概率水平上与更高精度概率水平上所得到的可区分域之间的关系。

4 应用案例

由于在投资过程中存在许多不确定性的风险因素，因此，许多风投公司为规避风险都在竞相寻找优质的风险投资项目，以最大化确定性收益。随着时间的推移，风险投资项目库在不断更新，对于投资决策方来说这些风投项目不是一成不变的，随着外界市场等因素的变化，一些旧的项目可能会从风投识别评估系统中删除，一些新的投资项目可能会得到投资方的青睐而添加到风投识别评估系统中。因此，决策方对预备项目进行评估，及时为风险投资者规避风险、减少损失显然非常重要。

利用双向S-优势概率粗集理论，在项目方案的各风险参数已经分析获取的基础上，对所知项目的风险程度进行识别评估。首先，通过用已获取的数据样本对风投识别评估系统进行训练，然后，再对现实中出现的新项目进行考察分类。

假设某风投公司一段时间内的系统项目训练样本集构成论域 U={x1，x2，…，x8}，此算例中考虑 5 个主要风险因素，分别是环境影响度（i），年化收益率（b），成长性（g），固定投入成本（k）及风险程度（d），其中，i，k相对应的属性值越大代表风险越大，b，g相对应属性值越小则代表风险越大，取条件属性集 Q={i，b，g，k}。由于项目类型不同，其环境影响度、年化收益率、成长性、固定投入成本一般不同，投资方所承担的风险程度也不同。令风险性程度d为该系统的决策属性，风险程度由大到小依次为 6、5、4、3、2、1，如表 1 所示。

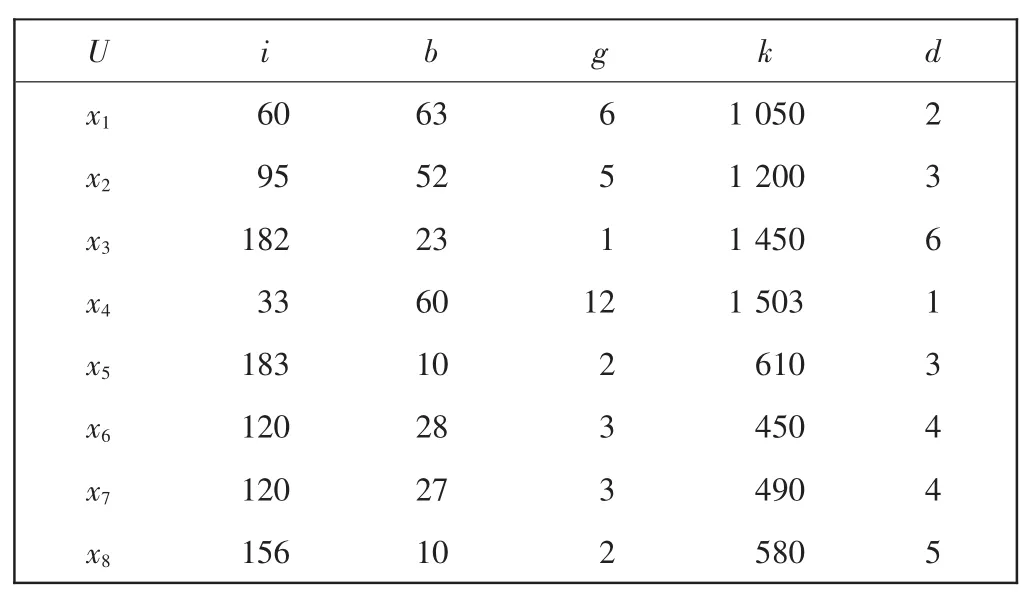
表1 风投识别系统的训练数据样本Tab.1 Training sample data of VC recognition system

在风投项目评估过程中，将所考查项目按风险程度分为两类，一类是具有高危破产性质的项目，另一类是不具有高危破产性质的项目。实际情况下，假定风险性程度不低于4的项目具有高危破产性，即在决策属性 d 下的向上累积集合中的项目具有高危风险性，则各项目的优势集分别为。

由定义3可得，集合cl4≥的下近似集为={x3}，则可得的“至少”决策规则如下。

规则 1if i≥182∧b≤23∧g≤1∧k≥1 450，then→x∈cl4≥。

由于形势发生了变化，涌现出不同于以往的新项目，如出现了新项目x′，x″，其条件属性值分别是：i=179，b=19，g=2，k=1 440；i=122，b=28，g=3，k=900。将这些参数与规则1匹配后发现，不能判定新项目是否具有高危风险性。然而，随着时间的推移，新项目x9受人青睐而迁入到训练样本项目中，其条件属性值为i=177，b=20，g=2，k=1 430，而原有旧项目 x1，x7由于长期无人问津而从系统中被移出。于是，由更新后的样本项目数据库可得到双向动态优势集={x3，x6，x8，x9}，而新的动态训练样本项目的优势集分别为：。

规则 2If i≥177∧b≤20∧g≤2∧k≥1 430，then→x∈cl4≥*。

根据规则2可确定项目x′属于高危风险性项目，但此时对新项目x″仍然无法判断。在暂时无新增训练样本项目的情况下，可根据定义7即双向S-优势概率粗集的定义（取α=0.8）计算得双向动态集合的下、上近似集分别为P0.8（DQ，Γ）o（）={x3，x6，x9}，P0.8（DQ，Γ）o（）={x2，x3，x6，x8，x9}，则再新添如下“至少”决策规则。

规则 3If i≥120∧b≤28∧g≤3∧k≥450，

由规则3可判定新项目x″亦具有高危风险性。综上，建议投资方需谨慎考虑对新项目x′，x″的投资决策。更进一步，由近似精度的定义可求得

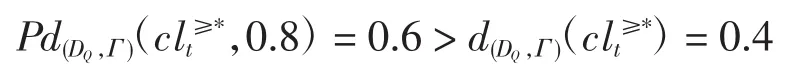
此结果恰好验证了定理2的结论。

综合上述分析可知，双向S-优势概率粗集模型比双向S-优势关系粗集模型分类更加精确细致，同时又可排除一些扰动数据对决策的影响，使决策更加符合实际需要。

5 结语

基于Pawlak和Shi等人有关研究工作[12]，结合S-概率粗集模型的动态统计特性及传统优势关系粗集模型[12]的分类特点，提出了双向S-优势概率粗集模型，该模型可针对含有偏序关系的动态数据系统进行数据分析和数据挖掘。由于在知识分类中充分利用了对象优势集的统计信息，因此，新模型与S-优粗集模型相比既增加了一定的容错和抗噪声能力又提高了分类精度和分类的合理性。利用新模型可获得具有较高准确性和适用性的规则。下一步的工作即是在所提出的新模型基础上，进一步研究不确定性度量问题及相应的规则提取算法，为实际应用系统开发奠定理论和算法基础。