含孔复合材料层合板的应力集中分析

卿光辉，王绍波

（中国民航大学航空工程学院，天津 300300）

复合材料层合板以其高于钢铁材料的比强度、比刚度、良好的抗疲劳、抗腐蚀性能和可设计性的优势，在航空航天、交通、化工等工程领域得到日益广泛的应用。在工程结构中，板壳结构的开孔不可避免。由于复合材料板壳类力学特性的特殊性，与各向同性材料板壳相比，含孔复合材料层合板壳的应力集中行为存在明显不同，无法求得含孔复合材料应力集中系数（SCF,stress concentration factor）的精确解。Lekhnitskii[1]推导了无限各向异性平板椭圆切口周围的应力应变分布，并给出了部分问题的理论解。Wu等[2]通过假设含孔有限正交各向异性板的近似应力分布，推导了含圆孔正交各向异性薄板应力集中的近似解析解。Chaudhuri[3]采用位移有限元法对复合材料层合板上孔周围的应力集中现象进行了研究。Paul等[4]采用位移有限元法对含单孔和两个同轴孔的纤维增强复合材料层合板在横向载荷作用下的应力和应力集中系数进行了研究。Kolosoff[5]计算了轴向均布载荷作用下无限长平板中椭圆切口周围的应力分布的近似理论解。Kumar等[6]利用位移有限元法研究了铺层角度和正交各向异性材料对含孔复合材料结构应力集中系数的影响。Kalita等[7]研究了横向荷载作用下中心开孔引起的挠度和诱导应力变化问题。王启智等[8]利用近似解析法与有限元法分析了受拉伸载荷下正交各向异性板含偏心孔应力集中系数的近似表达式。Xu等[9]基于经典板理论，应用复变函数方法得到了复合材料层合板中圆孔和椭圆孔应力集中系数的近似解析解。以上研究大多应用位移法来求解，但所得应力精确度不高，且不连续，仍需磨平处理，导致精度不高且计算量过大。

Qing等[10]提出了一种8结点块体非协调广义混合单元（NCGEM,noncompatible generalized mixed finite element method），位移变量和应力变量均为有限元模型的未知量。其突出的优点是在进行数值分析时可对模型同时引入位移变量和应力变量的边界条件，理论简单实用。另一方面，该方法避免了传统混合法中系数矩阵主对角线上有零元素的问题，在不要求额外的稳定混合元方案的前提下，成功地解决了传统混合法中位移和应力结果震荡的问题。实践表明：该方法的数值结果收敛速度快，应力结果精度非常高。

借鉴文献[10]的思路，通过引入新的非协调位移模式，建立一种非协调广义混合元列式，并用于含孔复合材料层合板的应力集中分析。通过对算例进行求解，验证方法的精确性和适用性。为研究含孔复合材料应力集中问题提供了一种可靠的新方法。

1 基础理论

1.1 三维问题的广义H-R变分原理

其中：σ=[σxzσyzσzzσxxσyyσxy]T为应力向量；S为材料柔度矩阵；Δ为微分操作矩阵；u=[u v w]T为位移向量；V为结构体积；s为结构表面积为作用在表面s上的已知应力。

广义H-R变分原理可表达为

其中：σ为3个方向的应力；C为材料刚度矩阵；α∈[0，1]。

对于8结点块体单元，位移向量在空间域内离散后的表达式为

其中：N为插值函数矩阵；qe为单元结点的位移向量；Ne为形函数，Nei=（1+ ξiξ）（1+ ηiη）（1+ ζiζ）/8，i=1，2，…，8。

对于8结点块体单元，应力场与位移场的形函数相同，即

其中，pe为单元结点的应力向量。

在通常的有限元网格模型下，当式（2）中的α=0.25时，广义混合元法求解得到的数值结果精度最好[12]。此时，广义H-R变分原理可表达为

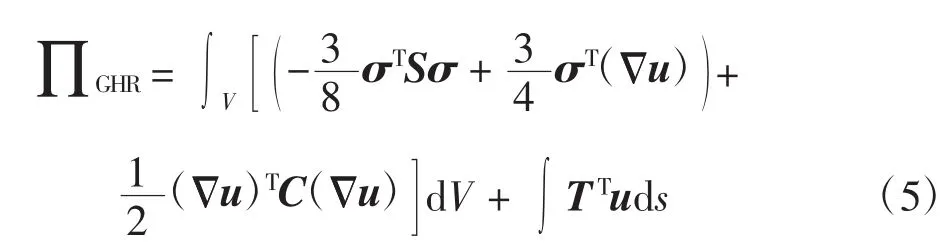
1.2 改进的广义非协调混合元列式

广义非协调混合元列式在广义协调混合元列式的基础上引入非协调项，可以看作对等参数单元的一种改进，目的是在计算量增加不多的情况下，提高单元的实际精度。一般的非协调位移场可表示为

其中：Nλ为对应于非协调位移场的形函数；λe为单元内部位移参数向量。

采用增强应变方法（EAS）[13]替代文献[11]中的非协调部分插值函数，即

其中，M为附加应变场的插值函数矩阵，即

其中：J为雅可比矩阵；J0为ξ=η=ζ=0时的雅可比矩阵；为6×6的矩阵；Mξ和T0的形式可参考文献[13]。

将非协调形式的位移场表达式（6）和应力场的近似表达式（3）代入广义H-R变分原理式（4）可得相应的离散形式为

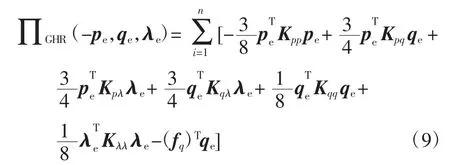
其中

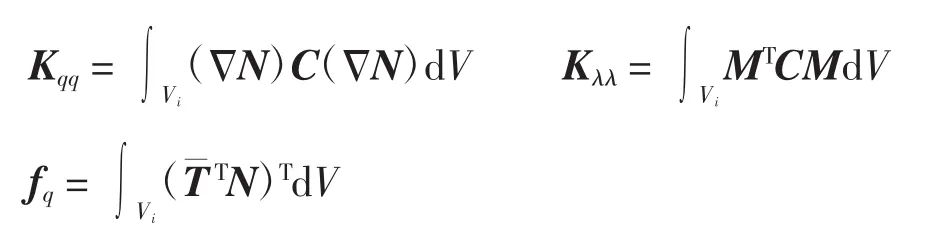
对上式的pe，qe，λe变分化简后得到改进的非协调广义混合元列式，即

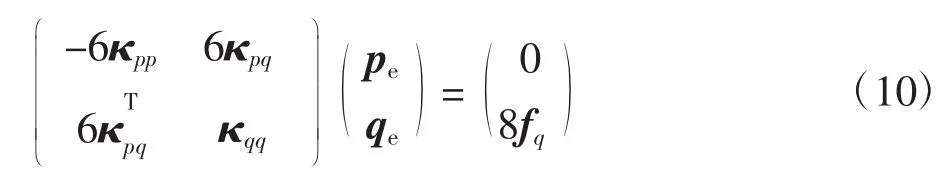
其中

2 数值算例

2.1 算例1

选取某各向异性含孔平板，物理尺寸如表1所示，材料参数为：E11=20 GPa，E22=9.2 GPa，μ12=0.341，μ21=0.157，G12=5 GPa，G13=5 GPa，G23=2.6 GPa。以下计算分析不同的板宽W和不同的孔直径d，可以得到d/W比，t为板的厚度。几何模型如图1所示。

表1 板的几何尺寸Tab.1 Geometrical size of plate

图1 各向异性带孔平板Fig.1 Anisotropic plate with hole

分别用非协调广义混合元法和商用软件ABAQUS计算各项异性含孔平板在E11和E22方向受到单向拉伸载荷时，点1处应力集中系数随d/W的变化分布，并与文献[2]中的结果比较，如图2、图3所示。

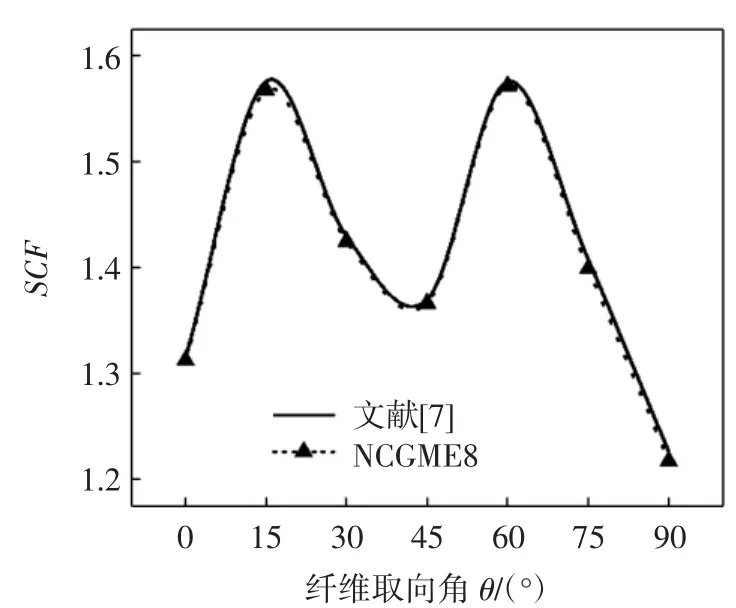
图2 单向拉伸载荷作用下的SCF（E11方向）Fig.2 SCF under uniaxial tension（in E11direction）

图3 单向拉伸载荷作用下的SCF（E22方向）Fig.3 SCF under uniaxial tension（in E22direction）

从图2和3可以看出，利用非协调广义混合元求出的应力集中系数均与文献[2]结果吻合良好，优于ABAQUS的结果。主要原因在于ABAQUS的求解和文献[2]的求解均采用位移法，一般通过本构关系求解应力变量，各结点的应力还需磨平处理，导致计算精度降低。而非协调广义混合模型中的应力形函数的阶次与位移形函数的阶次相同，且通过线性方程求得结点的解不需要磨平处理，故应力结果精度更高。

2.2 算例2

考虑文献[6]中的案例，分析某正交各向异性三层含孔层合板，各层所用材料不同，如图4所示。每层厚度为5 mm，共15 mm厚。长200 mm，宽100 mm。中心圆开孔直径20 mm。采用四边简支约束，并在x轴和y轴各加载1 MPa的力，3种正交各向异性材料的弹性常数如下：

材料 AE1=44.7，E2=17.9，E3=17.9，μ12=0.25，μ13=0.25，μ23=0.34，G12=8.96，G13=8.96，G23=3.45；

材料 BE1=39，E2=8.6，E3=8.6，μ12=0.28，μ13=0.28，μ23=0.28，G12=3.8，G13=3.8，G23=3.8；

材料 CE1=121，E2=112，E3=121，μ12=0.2，μ13=0.2，μ23=0.2，G12=44，G13=44，G23=44。

图4 三层5 mm层合板模型Fig.4 Three-layer 5 mm laminated plate model

根据文献[7]中对网格收敛性的研究，在模型划分为120个单元时，SCF达到了收敛值，误差约为渐近线的3%。该误差很小，计算时间最优。所以对比分析时也选择与文献[7]中的最佳网格尺寸。

本例给出了通过非协调混合元（NCGME8）计算3种正交各向异性材料中不同应力随纤维取向角θ变化的应力集中系数SCF的数值计算结果，并与文献[7]中的应力集中系数对比来验证该方法的准确性。图5～图10为根据不同面内应力求得的3种材料的应力集中系数。从图中可以看出，利用广义非协调混合元求得的应力集中系数与文献[7]中结果的误差最大不超过2%。

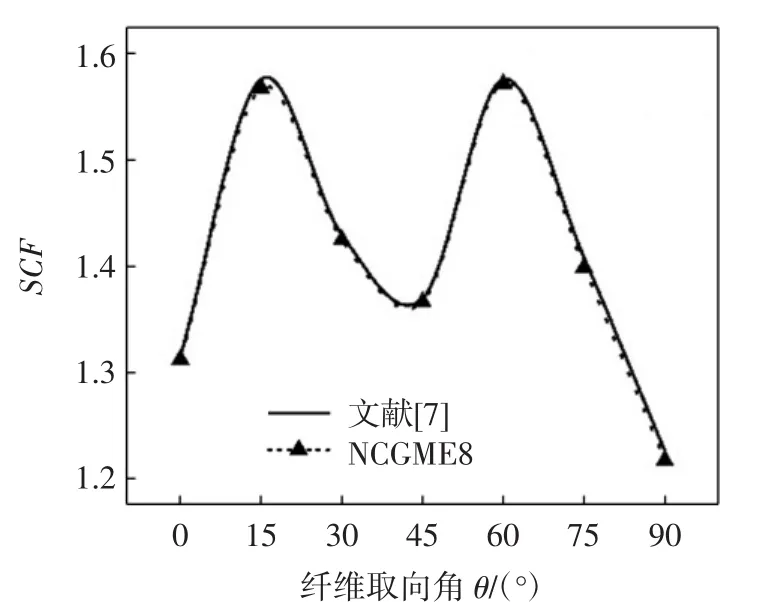
图5 根据σxx求得材料A的SCFFig.5 SCF of material A obtained by σxx

图6 根据σyy求得材料A的SCFFig.6 SCF of material A obtained by σyy

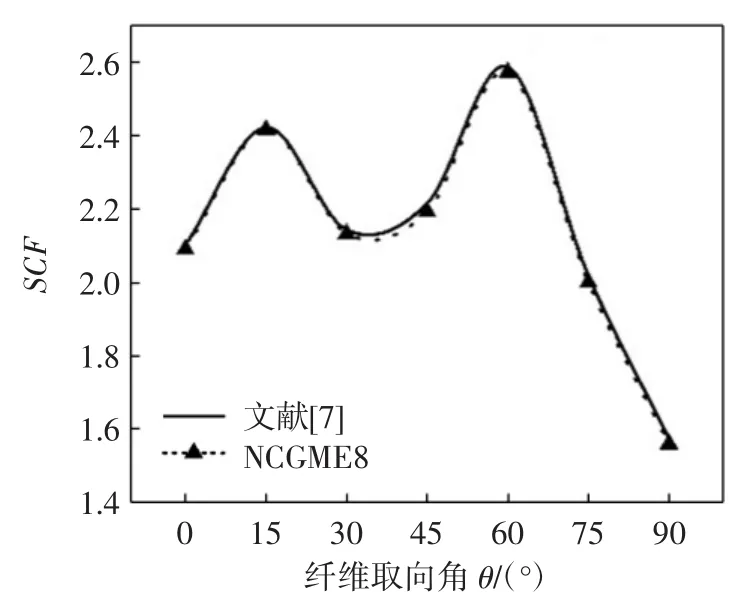
图7 根据σxx求得材料B的SCFFig.7 SCF of material B obtained by σxx

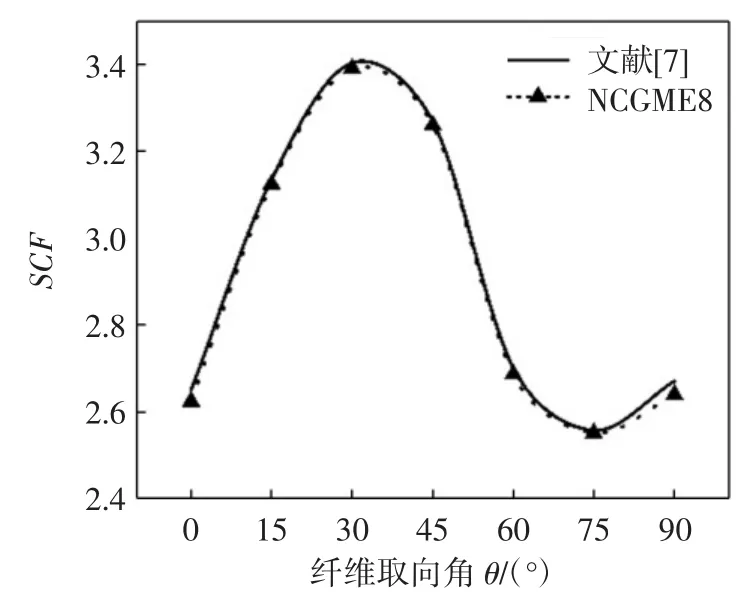
图8 根据σyy求得材料B的SCFFig.8 SCF of material B obtained by σyy

图9 根据σxx求得材料C的SCFFig.9 SCF of material C obtained by σxx

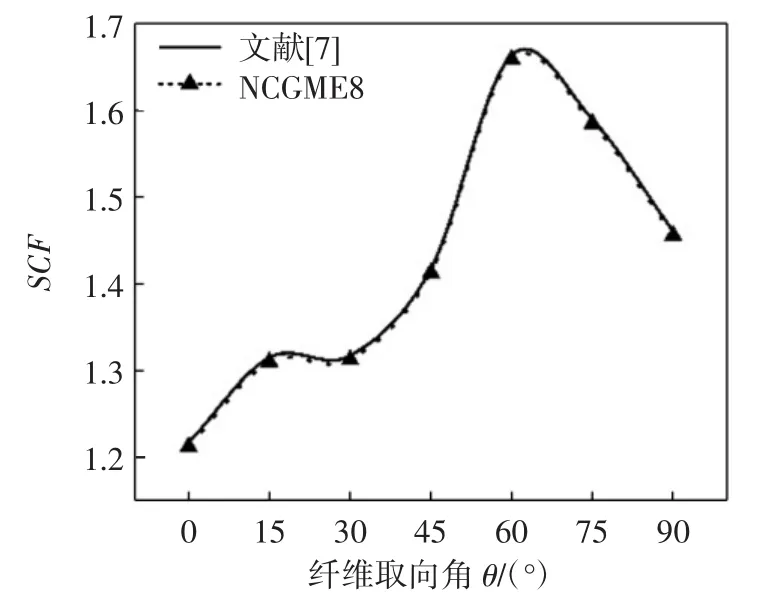
图10 根据σyy求得材料C的SCFFig.10 SCF of material C obtained by σyy

3 结语

首先提出了改进的广义混合有限元，然后将其用于分析含孔复合材料层合板板应力集中问题。结论如下：

1）改进的非协调广义混合有限元模型的基本理论及其推导过程简单；

2）应用该方法求解各类复合材料层合板板应力集中系数是可行的，数值结果可靠；

3）与常规的位移法类似，非协调广义混合有限元法具有广泛的适用性。

非协调广义混合法提高了SCF的求解精度，可有效预测由于应力集中现象而导致的含孔结构纤维断裂规律，为提高航空复合材料的抗疲劳、抗腐蚀性能提供理论参考。