基于分组的飞行器短期冲突对快速检测算法

关 静，张精卫

（1.中国民航大学理学院，天津 300300；2.浙江久立特材科技股份有限公司，浙江 湖州 313028）

在空中交通管制系统中，为了维护飞行器在空中的飞行秩序，保证飞行安全，相关决策部门必须根据不同的飞行环境，制定不同的飞行间隔标准，同时要求飞行员及管制人员必须严格按照相关的飞行标准执行[1]。近年来，随着民用航空及通用航空的快速发展，飞行密度不断增加，有效防止飞行器间发生碰撞，保证飞行器能够安全到达指定位置，以及保障飞行器能够遵循空中交通秩序使交通畅通成为空中交通管制的主要任务。而对飞行器的冲突检测[2]是保障飞行器和其他财产安全的重要因素，为空中交通管制工作提供决策支持。

国内外很多学者对飞行冲突实时检测算法进行了相关研究。Paielli等[3]提出了自由飞行情况下的短期冲突概率解决方案；Prandini等[4]和Hu等[5]提出基于航空器随机运动概率模型，并考虑随机扰动的冲突概率计算方法；Lygeros等[6]研究了结合飞行计划、航空器受气候变化影响情况下的冲突检测算法；Hwang等[7]进一步完善了航空器航迹的跟踪算法，在交互多模算法（IMM,interactive multiple models algorithm）的基础上提出残差均值交互多模算法 (RM-MM,residual-mean interacting multiple model algorithm)；李丹等[8]提出一种基于布朗运动的概率型空中交通冲突探测算法；王运锋等[9]提出航空器的位置差与速度差矢量内积小于0的航迹对才具有潜在冲突的理论，并根据安全飞行间隔规定，采用线性预测法对其进行冲突的有效性确认；王超等[10]提出飞机之间的模糊空间接近度概念及一种模糊冲突检测方法；徐伟等[11-12]提出了具有机动性检测的交互式UKF算法和卡尔曼滤波的分层检测算法；龚宏伟等[13]考虑了雷达数据的误差及气流等随机因素影响，将卡尔曼滤波引入飞行器短期冲突检测中，实现了更精确的预报；刘洋等[14]提出了一种概率型的短期冲突探测算法。边园飞等[15]在研究解决飞行器碰撞检测的有关问题中，通过减少参与检测的飞行器对，即减少检测次数来改进检测算法。

以上研究是从改进飞行器之间的冲突检测方法着手，提高单次检测的效率，并通过减少虚警和漏警的情况，解决冲突盲警告、轨迹不变等问题，提高算法的实用性。通过对上述研究分析，提出了一种基于分组的飞行器冲突对快速检测算法，研究处于同一飞行高度层的飞行器之间的飞行冲突检测问题。该算法依据飞行器最小水平安全间隔，对冲突对检测次数进行优化，在飞行器短期冲突检测中具有很强的实用性。

1 冲突对检测的快速算法

1.1 相关概念

定义1设S为飞行冲突待检测空域，Ai（i=1，2，…）是第i个边长为2l的正方形，若满足：

1）Ai∩Aj=，i≠j且 i，j=1，2，…；

2）A1∪A2∪…∪An∪…⊇S。

空域的划分是将整个待检测的空域S进行离散化的操作：划分之后的空域S被离散成若干个边长为2l的正方形待检测空域Ai（i=1，2，…）。若将待检测的目标空域S放入一个平面直角坐标系中，划分结果如图1所示。

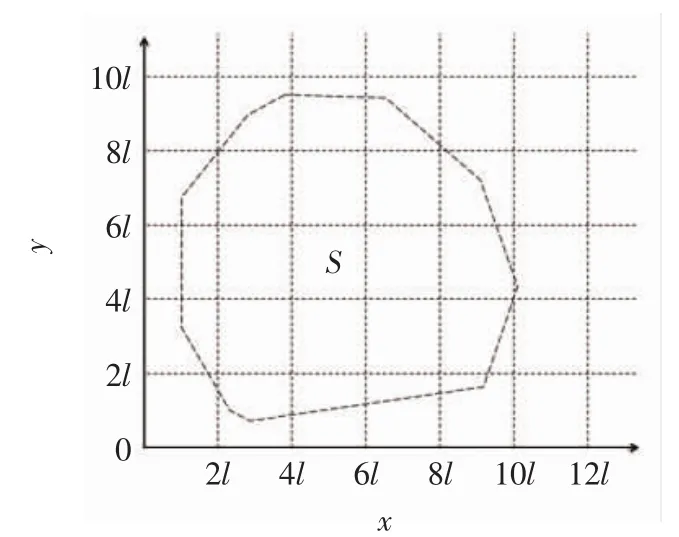
图1 正方形划分覆盖集Fig.1 Square divided cover set

定义 2对于点（x，y），其中 x∈[0，2l），y∈[0，2l），如果(x，y)满足下列条件：

2）存在一个 Ai，k∈（ki=1，2，…；k=1，2，…）满足对于任意的点（x0，y0），x0≥x，y0≥y，即（x，y）是 Ai，k的左下顶点。则称(x，y)为S的正方形划分覆盖集族。

正方形划分覆盖集族如图2所示。

图2 正方形划分覆盖集族Fig.2 Square divided cover set family

定义3对空域S上的任意两点（px，py）和（qx，qy），若满足

则称点（px，py）和点（qx，qy）为S上的一个冲突对，记作（px，py）↔（qx，qy）。

定义4对空域S中的全部冲突对组成的集合，称为冲突对集，记作（S）。

定理1任取则对S上任意的冲突对（px，p）y↔（qx，q）y，存在一个边长为2l的正方形A，其中使得（px，p）y∈A且（qx，q）y∈A。

证明 由于（px，p）y∈S，1为S上的一个正方形划分覆盖集，故存在一个A1∈1，使得（px，p）y∈A1。

如果（qx，q）y∈A1，则 A1即满足定理结论。否则，由于，所以（qx，q）y在B（ii=1，2，…，8）标示的范围中，标示形式如图 3 所示，其中Bi为A1周围外展1个单位的第i个区域。由1⊆可知：

若（qx，q）y∈B1∪B5，则存在A3∈3，使得（px，p）y∈A3，且（qx，q）y∈A3；

若（qx，q）y∈B3∪B7，则存在A2∈2，使得（px，p）y∈A2，且（qx，q）y∈A2；

若（qx，q）y∈B2∪B4∪B6∪B8，则存在 A4∈4，使得（px，py）∈A4，且（qx，qy）∈A4。

综上，定理得以证明。

定理2对任意的其中满足

图 3 （qx，qy）位置图Fig.3 （qx，qy）position

证明由于，故冲突对一致，即（S）。

1.2 哈希函数的构造

由定理2可知，只要对4个正方形划分覆盖集中的全部正方形区域分别进行冲突对探测，即可无遗漏的探测空域S中的所有冲突对。为了进行4个正方形划分覆盖集中的全部正方形区域的冲突探测，首先要将空域S中的探测目标按照所在的正方形分组。对于每个探测目标，在4个正方形划分覆盖集中，分别存在1个正方形包含该目标，因此需要将该目标分别归入4个组，并在这4个组中进行冲突探测。

为了能快速的进行分组，算法需要构造4个不同的哈希函数，使得哈希函数的值与正方形一一对应。

不妨假设，任意的点（x，y）∈S，x∈[0，2ml]，y∈[0，2ml]，其中m为正整数，则可以构造4个哈希函数分别为

其中：[]表示取整；n，p 为整数，且 n ＞（m+1），p ＞ n2。

显然，如上所构造的4个哈希函数可映射到4个正方形划分覆盖集中的全部正方形，且在空域S内不重复。

1.3 基于哈希表的改进算法

计算过程中，通常用以哈希值为索引的哈希表[16-17]来实现快速检索。检测中将空域S内待测目标的分组按照前文所述的哈希值建立哈希表，则在一个完整探测周期内，可以按照以下步骤进行冲突探测。

步骤1获取待测空域内所有飞行器信息，将其位置信息映射到S内的点（x，y），并分别代入4个哈希函数中得到哈希值，根据所得的哈希值在哈希表上快速检索到对应的目标组，将飞行器的信息分别插入到这4个目标组中，即实现待探测目标的分组。

步骤2对每个目标组进行冲突探测，即两两进行距离判断，找到各目标组的所有冲突对。

步骤3合并各个目标组探测得到的全部冲突对信息，即除掉其中可能重复的冲突对。

步骤4输出合并的结果，即为待测空域S内的所有冲突对。

2 数值算例及分析

2.1 算法实现

算法的开发环境：VisualStudio2005Express。飞行器、飞行器集合、冲突对等数据模型可方便地用C#语言面向对象的方式来表示，实现算法所需的4个哈希函数，并以SortedDictionary泛型类实现哈希表。SortedDictionary泛型类不仅能够将哈希值作为关键字与飞行器集合数据建立对应关系，还对哈希值关键字进行了排序，这样使关键字的检索效率大幅提升。考虑到哈希值的范围，用64位有符号整数作为哈希值的类型。为不失一般性，假设检测空域长宽均不超过5 000 km，最小安全间隔按10 km计算，即l=10，分别取n=500，p=300 000可满足算法要求。

为了进行分析比较，实验程序中也设计和实现了传统的冲突对检测算法，该算法对全部的飞行器进行逐对检测，这样能够保证其输出的冲突对结果是准确可靠的。

检测空域中的飞行器位置采用随机的方式生成样本，随机样本散点图如图4所示。样本数据可以由任何工具生成并记录在ASCII编码的数据文件中，以便在算法运行时加载和使用。

考虑到算法中执行次数最多的是一对飞行器之间的冲突检测，为了更准确地评估算法的效率，算法中增加了计数器以记录实际计算距离和判断冲突的次数。

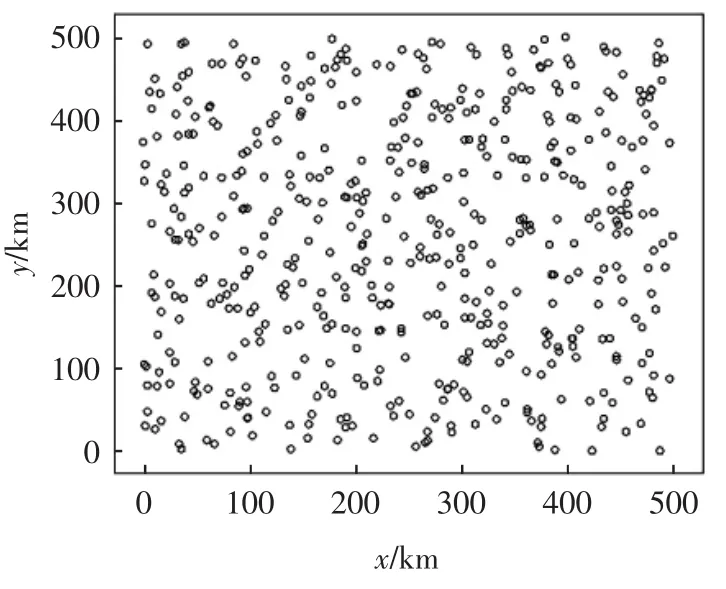
图4 一组500个飞行器样本的散点图Fig.4 Scatter plot of a group of 500 aircraft samples

2.2 结果及分析

经过对不同样本的多次仿真实验，基于分组的飞行器冲突对快速检测算法所输出的冲突对与传统算法输出的冲突对完全一致，从而验证了算法的正确性。

改变飞行器位置样本的规模，可观察到快速算法和传统算法判断次数的变化规律。在表1中列出了100～1 000个样本的判断次数记录，其判断次数与样本个数关系曲线，如图5所示。

表1 飞行器样本个数与判断次数记录表Tab.1 Record of aircraft sample and judgment times

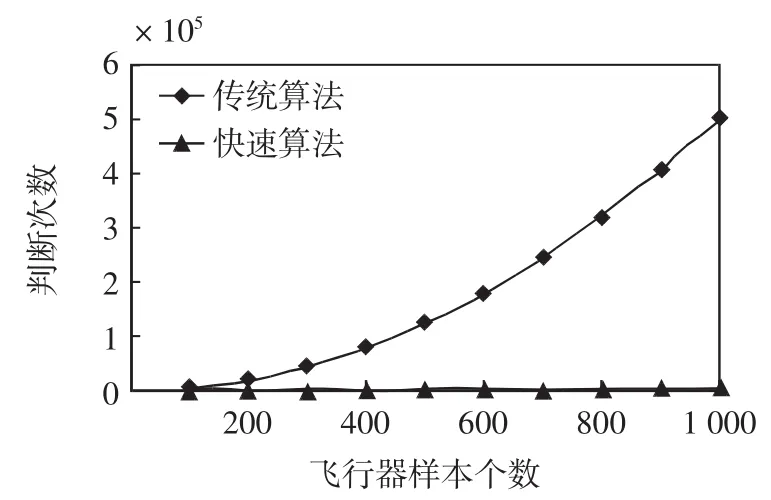
图5 飞行器样本个数与判断次数的关系图Fig.5 Aircraft sample number vs.judgment times

可见，在空域固定，检测目标分组数也固定的情况下，随着空域中飞行器数目的增加，传统算法和快速算法的判断次数都有所增加，但快速算法的判断次数的增长速度要远慢于传统算法。故相对于传统算法，待测空域中飞行器数目越多，快速算法的优势越明显。

如果空域的大小不一致，则按照前文描述的情况，由于目标的最小安全距离不变，检测目标的分组数也会变化，按照快速算法要求可相应地调整n和p的值，再进行计算。实验采用随机生成的方式，分别制作了不同尺寸空域中的飞行器位置样本，且为了研究需要，样本的数量都设置为500个。经过实验，分别记录了传统算法和快速算法的判断次数，记录结果如表2所示，随着检测空域的宽度变化，判断次数的变化曲线如图6所示。

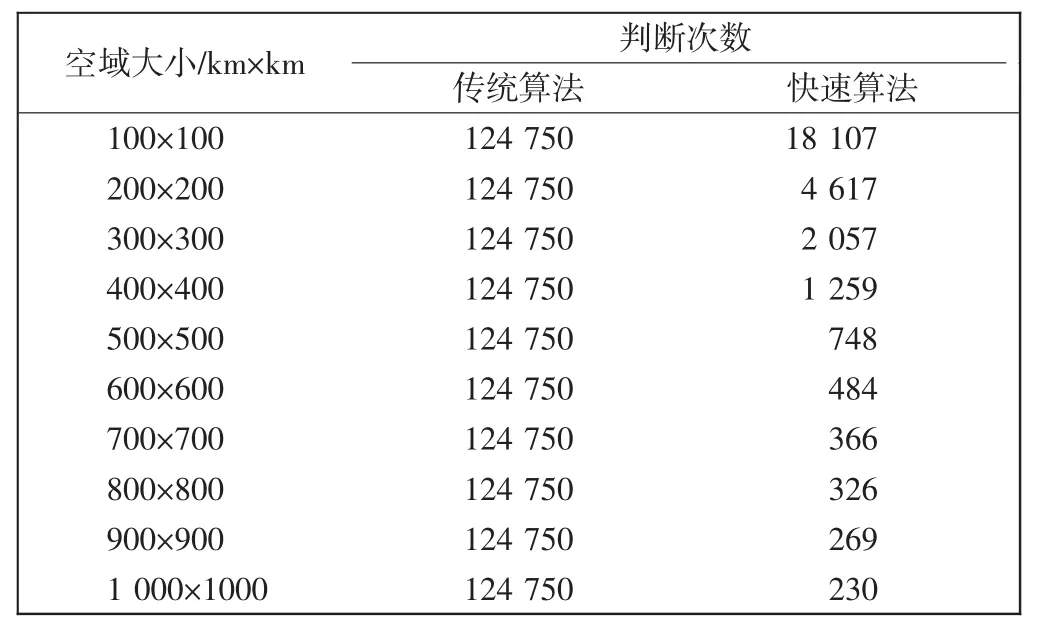
表2 空域大小与判断次数记录表Tab.2 Record of airspace area and judgment times

图6 空域大小与判断次数的关系图Fig.6 Airspace area vs.judgment times

可见，在空域中飞行器数目不变的情况下，空域增大时，传统算法的判断次数不会变化，而快速算法的判断次数却显著减少，即空域越大，快速算法的优势越明显。

综上，快速算法在应对大量检测目标、大范围空域的情况下相对于逐个判断的传统算法能够显著减少判断次数，大大缩短检测时间，提高检测效率，且结果准确无遗漏。

快速算法能够在判断次数上体现出上述优势，是由于对检测目标进行了合理的分组。不妨假设空域S中有k个待测目标，则不难求出按照传统算法，判断次数应为

假设1个正方形划分覆盖集用m个正方形覆盖了空域S，则m可视为空域S尺寸的关键指标。按照快速算法的要求，每个正方形中平均包含的检测目标数量为个，易知单个分组的平均判断次数为次，而按照算法要求，总共有4m个分组，因此总判断次数为

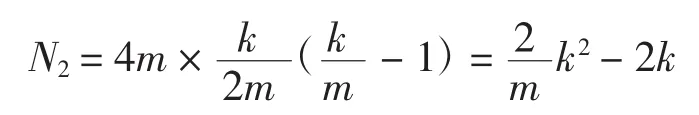
综上可看出：当空域增大时（即m增大），快速算法相对于传统算法判断次数会迅速减少，这主要是由于空域增大时，如果检测目标分布均匀，则距离就会拉大，从而最终通过分组只有极少的目标之间还需进行判断；而空域不变时，若检测目标数量足够大，则快速算法带来的效率提升仅与空域的尺寸有关，空域越大，提升越明显，这主要是由于对检测目标进行了分组，而如前文所述，按照快速算法要求进行的分组并不会造成冲突对遗漏。

3 结语

结合算例的仿真模拟将基于分组的飞行器冲突对快速检测算法与传统算法相比较，验证了快速检测算法能够在无遗漏检测的基础上，进一步提高检测的效率，提高飞行冲突检测的实时性。同时在解决虚警、冲突盲警告和轨迹不变等问题时，在冲突检测算法中选用判断参与检测的飞行器是否存在冲突风险的方法变得越来越复杂的情形下，快速检测算法的优势将会更加突出。